多目标微分进化改进算法及应用
2012-02-03刘长良
刘长良 于 明
(华北电力大学控制科学与工程学院,河北 保定 071003)
多目标微分进化改进算法及应用
刘长良 于 明
(华北电力大学控制科学与工程学院,河北 保定 071003)
微分进化算法作为一种新型、简单、高效的并行随机优化算法,近年来在许多领域得到了应用,多目标微分进化便是其中的一种。针对传统多目标微分进化算法中微分进化控制参数不能自适应调整、算法容易出现早熟和退化的现象,采用惯性权重参数自适应调整的控制策略以及改进的拥挤距离算法对多目标微分进化进行改进,并将改进后的算法用于控制系统PID参数优化仿真试验。结果表明,改进后的多目标微分进化算法具有较好的收敛性和分布性以及较高的搜索效率。
多目标 优化算法 微分进化 自适应 参数优化 PID
0 引言
控制系统PID参数优化属于多目标优化的问题,因其各个目标函数之间存在相互竞争的关系,采用单目标优化往往不能统筹兼顾,从而造成控制质量的下降[1]。虽然目前国内外广泛采用传统工业过程调节PID控制方法,但对控制器参数进行人工整定不仅需要熟练的整定技巧和经验,而且当被控对象特性发生变化时,控制器参数没有相应的自适应调节能力。
多目标进化算法(multi-objective evolutionary algorithms,MOEAs)的研究始于 20 世纪 80 年代[2]。在其研究过程中,由Deb等人提出的NSGA-Ⅱ算法以及由Zitzler等人提出的SPEA-Ⅱ算法应用较多[3]。自Rainer Storn和Kenneth Price于1995年提出了一种更有效、更简便的微分进化算法(differential evolution,DE)以来,许多学者致力于将其扩展应用到多目标进化领域的研究中,先后出现了PDE、PDEA、MODE和DEMO 等算法[4-7]。
以上这些多目标进化算法均旨在追求收敛性和多样性这两个优化指标,并且这些算法基本上都用到了以下两种策略:①通过构造Pareto候选解集保留所获得的非劣解,并通过适当的措施(空间分布密度信息)来维持解的多样性;②依据解集中个体间的Pareto支配关系和空间密度信息来确定个体的优劣[8]。但由于基本微分进化算法存在控制参数不能自适应调整的问题,参数的人为设定难以使寻优效果达到最佳;算法中的贪婪选择策略导致选择压力过大,并且当种群中决策变量中的某一维趋于相同时,微分向量为零[9]。这些因素都使得种群产生“早熟”问题。
1 基本微分进化算法
基本微分进化算法(DE)是一种基于种群优化的进化算法,它在求优过程中具有高效性、收敛性和鲁棒性等优点[10],适用于无约束连续变量的全局优化。
基本微分进化算法的进化过程包括变异、交叉和选择三个基本操作。以一个规模为NP的种群为例,其中的个体均为N维向量,第i个个体定义如下:

1.1 变异操作
在第G代中,目标个体向量为Xi,G,而变异后的个体向量为Vi,G。变异操作过程有多种方法,本文采用如下变异策略。
式中:DE为算法名称;rand为随机函数;r1、r2、r3为介于1和NP之间互不相同的随机整数;F∈(0,1),为变异算子,用于控制变异的幅度,即差值的放大倍数。

1.2 交叉操作
为了维持种群个体的多样性,在此引入交叉操作的方法,即由目标向量和变异向量不同基因位的数值,重新组合产生试验向量 Ui=(u0,i,…,uN-1,i)T。交叉操作的产生方法具体如下。

式中:G代表“第 G 代”;rand为随机函数,randj[0,1]为在0和1之间产生的一个随机数,j=0,1,…,N-1;jrand∈[0,N-1];CR为交叉算子且为介于0和1之间的连续实数,如果CR的值较大,DE的收敛速度会加快;如果CR的值较小,DE的鲁棒性会更好,但会增加问题的执行时间。式(3)是二项式交叉算子,许多文献经常采用这种形式。
1.3 选择操作
新一代个体的产生方式为:
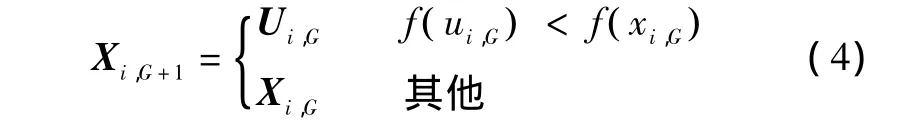
式中:f()为待优化的目标函数。在此过程中如果新产生的子代个体的适应度比父代强,即子代个体更优良,那么Ui,G将取代其相应的父代个体进入种群,参与下一代的进化。
2 改进的多目标微分进化算法
2.1 多目标优化问题
在多目标优化问题(multi-objective problem,MOP)中,某个目标性能的提高常常是以损害其他目标为代价,因而只能在多个目标之间进行折衷处理,以达到整体最优。在MOP中,常用定义如下。
① Pareto占优
A<B(A占优B),当且仅当:
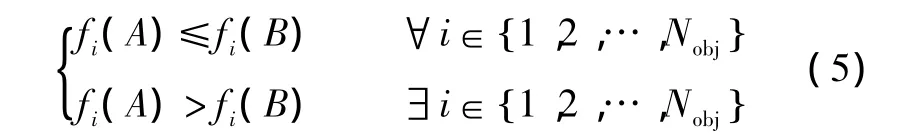
式中:A和B为决策空间中两个不同的个体。
② Pareto最优或Pareto非劣
A是Pareto最优解(非劣解),当且仅当:
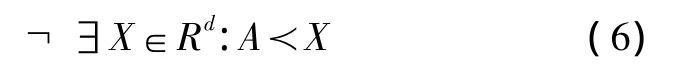
式中:d为向量维数。
所有Pareto最优解的集合称为Pareto最优解集;Pareto最优解对应的目标函数值称为非劣目标向量;所有非劣目标向量形成的区域称为Pareto前沿。多目标优化问题的求解实际上是找到尽可能多的Pareto最优解,且使其相应的目标向量在Pareto前沿中均匀分布[11]。
2.2 改进的多目标进化算法
2.2.1 控制参数调整策略
在微分进化算法中,控制参数的设置与调整是一个重要且困难的问题,目前还没有一种惯行的控制参数设置与调整机制。针对上述问题,许多文献提出了控制参数自适应调整的策略,如采用模糊自适应的参数调整方法和依据群体适应度方差对控制参数进行调整的方法等[12-13]。
本设计采用粒子群算法中惯性权重动态调整思想来动态调整DE中的变异因子F和交叉因子CR[14]。在搜索的初始阶段,由于个体随机分布在解空间中,因此,向量差值较大,这就要求算法的控制参数F相对小一些。但随着种群的不断进化,个体逐渐靠近最优个体,算法中变异操作产生的差值扰动会逐渐变小,这就要求此时的F相对大一些,使得变异操作后的向量能够开拓新的搜索空间。同样,对于交叉因子CR也是如此。基于以上分析,本文采取的控制参数调整策略为:

式中:Fmax和Fmin分别为变异因数F的最大值和最小值;lmax和l分别为设定的最大进化代数和当前的进化代数;CRmax和CRmin分别为交叉因数CR的最大值和最小值。
2.2.2 拥挤距离算法改进
NSGA-II算法依据同一个Pareto非劣排序等级中拥挤距离大的个体被保留的原则进行选择操作。设个体B的前后相邻两个个体分别为A和C,拥挤距离(稀疏度)DC(B)定义如下:

式中:fi(A)与fi(C)分别为个体A和个体C在第i个目标函数上的值。边界个体的拥挤距离定义为无穷大,保证无条件进入下一代。拥挤距离计算示意图如图1所示。
图1(a)~图1(c)为两目标优化问题,A、B、C处于同一个Pareto非劣排序等级。很明显,个体B在图1(a)中的稀疏度均优于图1(b)与图1(c),但按原始的拥挤距离算法不能判别出个体B在图1(a)和图1(c)中的优劣。这样,随着进化代数的增加,会导致解的分布性和多样性劣化[11]。由此可见,这种算法存在较大的局限性。
改进后的拥挤距离算法示意图如图1(d)所示,设O为A和C的中心点。改进的拥挤距离DC(B)计算方法如下:

式(10)反映了个体稀疏度既与其在目标函数上邻域的大小[fi(A)-fi(C)]有关,又与分布均匀程度[fi(B)-fi(O)]有关,由此判断出个体B在图1(a)中的稀疏度要优于图1(c)。

图1 拥挤距离计算示意图Fig.1 Calculation of the crowded distance
改进的多目标微分进化算法流程图如图2所示。

图2 改进算法流程图Fig.2 Flowchart of the improved algorithm
3 仿真研究
3.1 过热蒸汽温度优化模型
火电厂过热蒸汽温度对象具有大惯性、大延迟、非线性和时变的特性。影响过热蒸汽温度的因素有很多,如机组负荷、火焰中心位置、给水温度、烟温和流速、减温水流量等[15]。目前,通常采用的串级汽温闭环控制系统结构如图3所示。

图3 串级汽温闭环控制系统结构Fig.3 Structure of the cascade closed-loop steam temperature control system
图3中,内回路为PI控制器,外回路为PID控制器,W1(s)为惰性区传递函数,W2(s)为导前区传递函数,d1和d2分别为输出测量干扰和控制量干扰,yr为给定值,y为输出测量值。
某一超临界600 MW直流锅炉高温过热器在75%负荷下,主汽温对喷水扰动的动态特性为[16]:
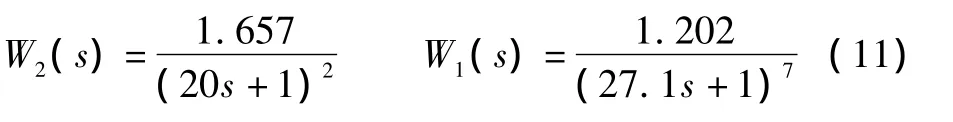
优化工作的任务就是应用改进的多目标微分进化算法对PID控制器的比例Kp、积分Ki和微分Kd在其可行域空间内进行寻优,使系统能稳定运行,且上升时间tr、超调量σ(%)和调节时间ts的组合达到最优。显然,这三种性能指标是相互竞争的关系。只有采用多目标优化,才能克服传统单目标方法中的性能退化问题,以达到综合最优的控制效果。
3.2 改进算法仿真研究
在本算例中,Kp、Ki和Kd的取值范围分别为[0.001,4]、[0.001,2]和[0.001,50]。内环为 PI调节,控制器参数固定为比例增益Kp2=10、积分增益Ki2=0.1[16]。设定汽温最大允许超调量为5%,系统稳定时间不大于600 s,上升时间不超过300 s,仿真时间为2 500 s。
改进的多目标微分进化算法的参数设置为种群规模100、进化代数500、交叉因子下限CRmin=0.1、上限CRmax=0.9、变异因子下限Fmin=0.1、上限Fmax=0.9。
经过500代的进化后,产生多组Pareto最优解,决策者在实际运行中只能从诸多Pareto最优解中选取一个作为最终方案。本文依据文献[11]中的模糊集理论方法来确定最优的折衷解。最终寻优结果为:

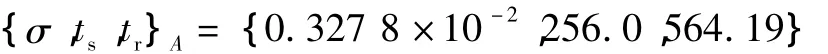
对于输出主蒸汽温度单位阶跃响应,应用改进的多目标微分进化算法对PID控制器进行参数整定后,得到的幅值响应与文献[16]粒子群算法和单目标优化得到的结果相对比,得到的主汽温阶跃响应曲线如图4所示,PID及阶跃响应性能参数如表1所示。

图4 主汽温阶跃响应曲线Fig.4 Step response curves of main steam temperature

表1 PID及阶跃响应性能参数Tab.1 Parameters of PID and step response performance
从表1可以看出,应用改进的多目标微分进化方法得到的曲线超调量明显小于应用单目标优化和粒子群算法得到的超调量,三者的峰值时间相差不多,但多目标微分进化方法仍优于后两者;然而对于调节时间来说,应用改进的多目标微分进化方法得到的结果却不及单目标优化方法。究其原因,正是多目标优化的特性所致,即一个优化目标性能的提高必然以其他性能劣化为代价。
总体来看,应用本文提出的改进的多目标微分进化方法得到的系统具有良好的鲁棒性,且能够仿真出超调量很小的响应曲线,调节时间和峰值时间也相对令人满意。
4 结束语
本文将微分进化算法与多目标优化相结合,并对传统算法的不足进行了改进。将改进后的多目标微分进化算法应用于主汽温PID控制器参数优化设计,实现了主汽温的多目标优化控制。从仿真结果可以看出,使用改进后的多目标微分进化算法优化得到的最优参数对主汽温进行控制,其阶跃响应过程表现出较好的动态特性和稳态特性,超调量、上升时间和调节时间三个目标函数均得到了较好的优化,获得了最优的综合控制效果。
由此可见,即使对于火电厂过热蒸汽温度对象这种具有大惯性、大延迟、非线性和时变特性的复杂系统,改进的多目标微分进化算法也能获得良好的优化效果。因此,进一步探索和研究多目标微分进化算法对于这种需进行多目标优化的复杂控制系统具有极其重要的意义。
[1]李玥,孙健国.基于遗传算法的航空发动机多目标优化PID控制[J].航空动力学报,2008,23(1):174-178.
[2]崔逊学.多目标进化算法及其应用[M].北京:国防工业出版社,2008.
[3] Hui Qin,Zhou Jianzhong,Li Yinghai,et al.Enhanced strength pareto differential evolution(ESPDE):an extension of differential evolution for multi-objective optimization[C]//Fourth International Conference on Natural Computation,2008:191-196.
[4] Liu Zifa,Zhang Jianhua.An improved differential evolution algorithm for economic dispatch of power systems[C]//Proceedings of the CSEE,2008:100-105.
[5] Yang Guangya,Zhao Yangdong,Kit P W.A modified differential evolution algorithm with fitness sharing for power system planning[J].IEEE Transactions on Power Systems,2008,23(2):514-522.
[6] Gao Yuelin,Liu Junmin.A modified differential evolution algorithm and its application in the training of BP neural network[C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics,2008:1373-1377.
[7] Zhang Xuexia,Chen Weirong,Dai Chaohua,et al.Self-adaptive differential evolution algorithm for reactive power optimization[C]//Fourth InternationalConferenceon NaturalComputation,2008:560-564.
[8]张利彪,周春光,马铭,等.基于极大极小距离密度的多目标微分进化算法[J].计算机研究与发展,2007,44(1):177-184.
[9] Fan Jishan,Wu Shengxiong,Wang Jingzhuo,et al.IMODE:Improving multi-objective differential evolution algorithm [C]//Fourth International Conference on Natural Computation,2008:212-216.
[10]阳明盛,罗长童.最优化原理、方法及求解软件[M].北京:科学出版社,2006.
[11]彭春华,孙惠娟,郭剑峰.求解PMU多目标优化配置问题的非劣排序微分进化算法[J].控制理论与应用,2009,26(10):1075-1080.
[12]Brest J,Greiner S,Boskovic B,et al.Self-adapting control parameters in differential evolution:a comparative study on numerical benchmark problems[J].IEEE Transactions on Evolution Computation,2006,10(6):646-657.
[13]刘自发,张建华.一种求解电力经济负荷分配问题的改进微分进化算法[J].中国电机工程学报,2008,28(10):100-105.
[14]周清清,刘勇.多目标优化微分进化改进算法的实现[J].自动化仪表,2009,30(12):6-9.
[15]李学斌.基于多目标遗传算法和多属性决策的主蒸汽温度PID参数优化[J].热力发电,2009,38(9):33-36.
[16]李剑波,王东风,付萍,等.基于改进粒子群算法的主汽温系统PID 参数优化[J].华北电学学报,2005,32(4):26-30.
Improved Multi-objective Differential Evolution Algorithm and Its Application
As a new type of simple and efficient parallel stochastic optimization method,the differential evolution algorithm has been applied in many fields in recent years and multi-objective differential evolution is just one of them.In traditional multi-objective differential evolution algorithm,the differential evolution control parameters cannot be adaptively adjusted,thus the algorithm is easy to be precocious and degraded.By adopting the control strategy of inertia weight parameter adaptive adjustment and the improved crowding distance algorithm,the multiobjective differential evolution is improved.The improved algorithm is used in simulation experiment for parameter optimization of PID control system.The result indicates that the improved algorithm features better convergence,distribution and high search efficiency.
Multi-objective Optimization algorithm Differential evolution Self-adaptive Parameter optimization PID
TP18
A
国家863计划基金资助项目(编号:2007AA041106)。
修改稿收到日期:2011-03-30。
刘长良(1966-),男,2002毕业于华北电力大学自动化专业,获博士学位,教授,博士生导师;主要从事火电机组热工系统建模与控制方面的研究。
