基于FPGA的等精度转矩转速测试仪

梁龙学 杜永文

(兰州交通大学电子与信息工程学院，甘肃 兰州 730070)

0 引言

传统转矩转速测试仪对被测信号一般沿用“高频用测频法、低频用测周法”。这种做法对提高测量精度无疑是十分有效的，但却存在测量精度的离散性问题［1］，且在整个测试范围内测试精度差异很大，降低了测量结果的置信度;测试适用范围小，一种仪器只能接一种型号的传感器，缺乏通用性;需用测频法及测周法分段测试，给用户的操作和使用带来极大不便;虽有在线测试方案［2］，但误差太大。为此，本文提出一种等精度的、通用性强的转矩、转速测试方案。

1 测试仪组成及测量原理

转矩转速测试仪由转矩转速传感器(如JN338)、光电隔离、电子开关、FPGA、单片机、键盘和显示等部分组成。JN338负责信号采集，它能将旋转动力系统或机电一体化设备的转矩、转速等被测信号转化为标准的TTL数字信号。FPGA负责对上述数字信号的频率进行精确测量，并送至单片机进行处理并显示。单片机通过控制电子开关选取测试对象，同时还控制FPGA的采样速率和测量方式等。转矩转速测试仪整体结构如图1所示。

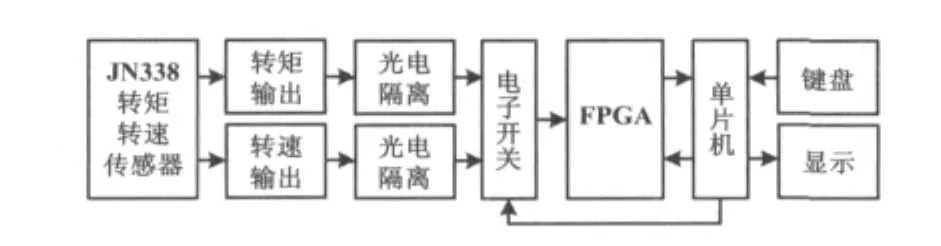
图1 转矩转速测试仪结构图Fig.1 Structure of torque and speed tester

1.1 转矩转速测量原理

根据输出信号不同，转矩转速传感器可分为正弦波输出型和数字输出型两大类。如JN338为数字输出型，其输出信号可直接进行测试;它拥有20多种型号，且其总的转矩测量范围为1～5000 N·m，转速测量范围为10 ～60000 r/min。JN338测量原理简述如下［3］。

转速测量公式为:

式中:n为转速，r/min;f为实测转速输出信号的频率值，kHz;Z为传感器测速齿数。

在有效的量程范围内，传感器转矩输出信号频率与对应转矩值基本上呈线性关系。转矩输出信号频率在零点时，f0=10 kHz;正向旋转满量程时，fp=15 kHz;反向旋转满量程时，fr=5 kHz。转矩实际输出信号频率用f表示。则正向转矩为:

反向转矩为:

式中:Mp为正向转矩;Mr为反向转矩;N为转矩满量程。如JN338100型对应转矩测量范围为10～100 N·m，可测最高转速为6000 r/min，则公式中的N取100 N·m。

轴输出功率由转矩转速传感器输出的转矩及转速值经过运算得到。轴输出功率的计算公式为:

式中:P为轴输出功率，kW;M为实际转矩，N·m;n为转速，r/min。

1.2 信号频率的准确测量

由上述分析可知，转速和转矩的测量均与被测信号的频率有关，所以测试仪整体测量的准确度在很大程度上取决于信号频率的准确测量［4］。

直接测频法常用的有测频法和测周期法，但它们存在以下问题:±1计数误差不可消除;频率不同，测量精度不同，且差异很大;若用测频法、测周法分段测试，则频率衔接点难以选定，且存在测量精度跳变。采用等精度测频法可以克服上述缺陷。

1.2.1 等精度频率测量原理

等精度测频原理如图2所示。

图2 等精度测频原理波形图Fig.2 Waveform of the equal-precision frequency measurement

在等精度测频法中，闸门时间不是固定值，而是被测信号周期的整数倍，因此消除了对被测信号计数所产生的±1个字误差，并且达到了在整个测试频段内的等精度测量。

在测量过程中，需使用两个计数器分别对标准信号和被测信号进行计数。设在一次实际闸门时间t中计数器对被测信号的计数值为Nx，对标准信号的计数值为Ns，且被测信号周期、频率分别用Tx和fx表示，标准信号用Ts和fs表示，则有:

即被测信号的频率fx为:

具体测量过程为按下测量键，单片机即启动预置闸门开启信号(对应上升沿)，此时计数器并未开始计数，而是要等到被测信号的上升沿到来时，测频电路产生实际闸门开启信号，计数器才真正开始计数。同样地，预置闸门关闭信号(下降沿)到来时，计数器并不立即停止计数，而是要等到被测信号上升沿到来时，测频电路产生实际闸门关闭信号后才真正结束计数。显然，实际闸门时间t与预置闸门时间t1并不严格相等，但差值不会超过标准信号的一个周期［5－6］。

1.2.2 等精度频率测量误差分析

由式(6)可知，若忽略标频fs的误差，则等精度测频可能产生的相对误差为:

式中:fxe为被测信号频率的准确值。

在测量中，由于fx计数的启停时间都是由该信号的上升沿触发的，在闸门时间t内对fx的计数Nx无误差(t=NxTx);对 fs的计数 Ns最多相差一个数，即|ΔNs|≤1，Ns用 Ns+ΔNs修正后可得到被测信号频率准确值fxe的计算公式，即:

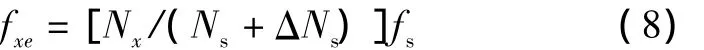
将式(6)、式(8)代入式(7)，经整理可得:

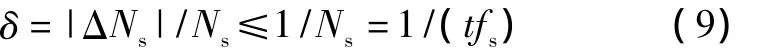
由式(9)可以得出以下结论:测量频率的相对误差与被测信号频率大小无关，仅与闸门时间和标准信号频率有关，即实现了整个测试频段的等精度测量;闸门时间越长，标准频率越高，测频的相对误差就越小［5－6］。选用 FPGA 时钟频率为 fs=60 MHz，如闸门时间取 t=1 s，则测试精度 δ≤1.7 ×10－8。

1.2.3 测试精度及相关参数

由式(5)可知:Ns=t/Ts=tfs，Nx=t/Tx=tfx。由于FPGA的fs(60 MHz)是固定的，Ns可根据t的值算出，而Nx随着被测信号频率fx而变，但其最小值也应为1(表示对一个完整的被测信号周期进行计数)。此外，根据采样定理，fx最大值应不大于fs/2，可相应地算出Nx的取值范围。δ由式(8)计算得出。测试精度与开门时间的关系如表1所示。

表1 测试精度等与闸门时间的关系表Tab.1 Relationship between testing precision and gate time

由此可见，在标准信号频率不变的前提下，闸门时间越长，Ns、Nx的计数值越大，测试精度越高，但测频范围基本不变(仅其能够测试的下限频率有所变化)。

1.2.4 计数器选择

JN338系列传感器转矩测量范围为1～5000 N·m，而转矩信号频率在正、反向旋转满量程时分别为15 kHz、5 kHz，故转矩信号频率低且变化范围小。

由式(1)可知，f=nZ/60。显然，n和Z越大，f也就越高。由于JN338转速测量范围为10～6000 r/min，其所对应的转速信号频率并不高。加上其他类型传感器，可得出目前传感器能够测量的最高转速为36000 r/min，编码器齿数Z最大为2700，由此可估算出转速信号频率最大值为 1.62 MHz，远小于 fs。

由此可见转矩、转速信号频率都不高，亦即Nx对应值不大。因此，计数器的位数选择主要取决于Ns。综合考虑，计数器取32位即可(232≈4.29×109＞6×108)。

2 转矩转速测试仪的设计

2.1 通用性设计的实现

由于采用等精度测频法后测试仪的测频范围很大(达30 MHz)，能够覆盖所有型号的转矩转速传感器的测试范围。为此，提出“一个主测试机箱配多种传感器”的设计思想——采用即插即用接口设计。具体来讲，就是用户根据被测对象转矩、转速变化范围选择型号合适的传感器，先将其固定在测试轴上，再将其转矩、转速输出引线插头分别接到对应插槽即可。数字式传感器(如JN338)可直接接入，而对正弦波输出类(如JCZ型)则需在接入之前将它们的输出信号转换为TTL电平［7］。这样，一个主测试机箱可配接不同型号的传感器，实现一机多用，既经济又方便。

2.2 等精度频率测量的实现

在快速测量的要求下，要保证较高精度的测频，必须采用较高频率的标准信号。单片机受本身时钟频率和若干指令运算的限制，测频速度较慢，而FPGA具有集成度高、工作频率高和功能强大等特点，能够满足高速、高精度测频要求。通过对FPGA进行设计，即可实现频率的等精度测量。测频主系统框图如图3所示。

图3中，A7～A0和B7～B0为两个计数器的计数值输出，单片机通过R1、R0数据读出选通端，读出4个8位(即32位)计数值，并根据一定算法算出频率和脉冲宽度。STR为预置门启动输入;F/T为测频/测脉宽选择;CH为自校/测频选择;Fa为自校频率输入端;Fs为标准频率信号输入端;Fx为经过放大整形后的被测信号输入端;END为计数结束状态信号［5］。由于只有一个信号输入端，为节省成本和简化设计，采用转矩、转速信号分别进行测试的方案，并由单片机程控电子开关来实现。这样，使用一片FPGA(EPF10K10LC84)即可完成各种测试功能。

图3 测频主系统框图Fig.3 Block diagram of the main system of frequency measurement

在MAX+plusⅡ软件环境下进行FPGA设计。首先对各功能模块进行逻辑描述，然后通过EDA开发平台，自发地对设计文件完成逻辑编译、化简、综合及优化、布局布线及仿真，最后对FPGA芯片进行编程，以实现系统的设计。系统顶层设计原理图如图4所示［6］。

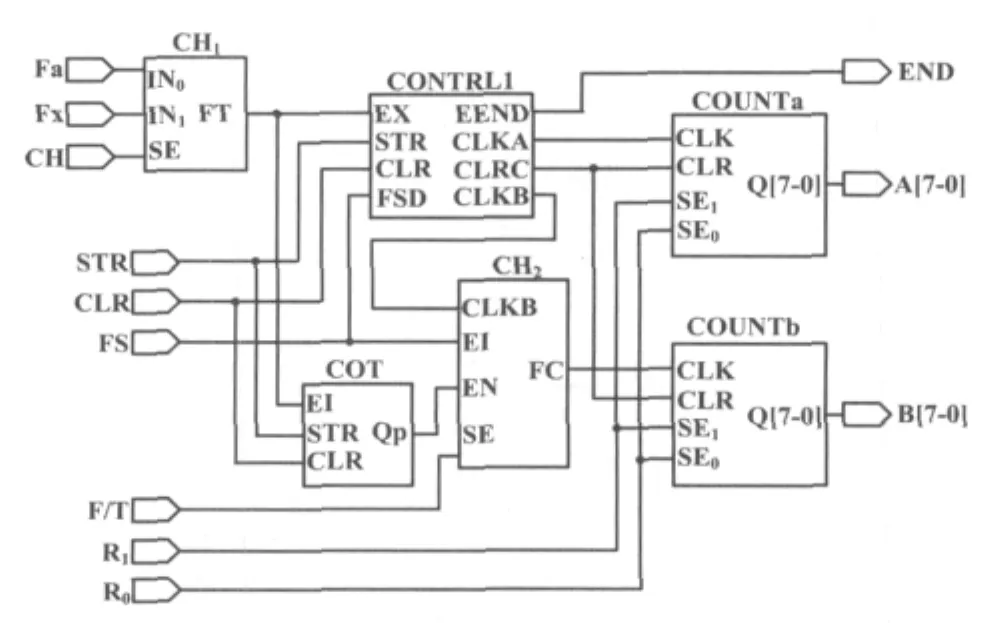
图4 系统顶层设计原理图Fig.4 Design principle of the top layer

图4中，CH1和CH2为选择器，CH1进行自校/测频选择，CH2进行测频和测脉宽选择。CONTRL1为控制模块，控制被测信号Fx和标频信号Fs的选通及2个32位计数器(COUNTa和COUNTb)的计数。计数器以4个8位二进制数形式输出。FPGA与SPCE061A单片机的接口比较简单。A7～A0和B7～B0与单片机A口相连接，其他输入/输出端与单片机B口相连接。

2.3 无法实现同相的情况处理

若其中一个被测信号和标准信号的周期是另一个的整数倍，且在进入系统时存在初始相位差，则它们经过一定时间t(预置闸门时间)后相位差仍保持不变，即二者相位可能永远不重合［8］。图5即表达了TX=3 Ts时，被测信号u和标准频率信号fs相位不重合这两种情况，其中 ux比fs相位超前，而uy比 fs相位滞后。由于无法找到同步点，这类情况显然不能采用等精度测频法。故在实际测试时，如经过一段时间t后实际闸门脉冲仍无法形成，即计数器无计数，则认为这两个信号无法实现同相。单片机判定后会自动改用直接测频法进行测量并提示用户。

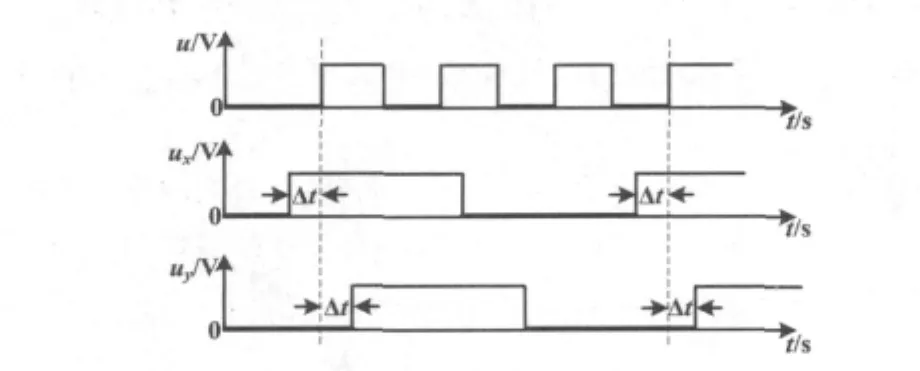
图5 被测信号和标准信号相位不重合的情况Fig.5 The situation of phase not coincide for measured signal and standard signal

2.4 单片机选型及设计

单片机选用SPCE061A。该单片机为16位机，数据处理能力较强;具有32 kB Flash和2 kB SRAM以及液晶驱动器，其液晶驱动可直接通过软件控制来实现，提高了系统的稳定性和抗干扰能力;I/O口数量多(A、B口各16个)，不需要扩展即能满足系统需要;时钟频率较高，约40 MHz。键盘设有自校/测频选择键CH、测频和测脉宽选择键F/T、预置门启动输入键STR、转矩测试键M、转速测试键n和打印键P等功能键。

由于需要显示转矩、转速、轴输出功率值以及闸门时间、测试精度、信号频率等诸多信息，显示器选用点阵数为320×240且带中文字库的LCD(如HTM320240G)。

3 结束语

本设计采用等精度测频法，实现了转矩、转速信号的等精度测量;采用即插即用接口设计，使测试主机具有更大的使用灵活性，大大增强了测试仪的通用性;利用FPGA工作频率高、功能强的特点简化了系统设计，提高了测试精度。经测试表明，本设计具有很好的推广及应用价值。

［1］杨冠群.以周期滑动扩展的测周法实现等精度的频率测量［J］.电子技术应用，2002，28(2):41 －43.

［2］刘海琴，史智兴，程天良，等.基于单片机的电机转矩测量系统设计［J］.微计算机信息，2006，3(2):27 －29.

［3］孟臣，李敏.JN338智能数字式转矩转速传感器及其应用［J］.国外电子元器件，2003(11):56－58.

［4］梁龙学.一种新型数字式转矩转速测试仪［J］.兰州交通大学学报:自然科学版，2006，25(1):101 －103.

［5］包明，赵明富，郭建华.基于FPGA的高速高精度频率测量的研究［J］.单片机与嵌入式系统应用，2003(1):31－33.

［6］王慧.基于FPGA高速高精度频率测量系统的实现［J］.传感器世界，2006，12(1):27 －29.

［7］梁毓明，汪锋锁，刘志刚.JCZ型转矩转速传感器输出信号的处理方法［J］.计算机测量与控制，2005，13(11):1296 －1298.

［8］刘德亮，王竹林，尉广军.基于FPGA高精度频率测量仪的设计［J］.河北工业科技，2010，27(1):29－31.