一类具有周期扰动的向日葵方程的次调和分支
2012-02-03殷红燕
殷红燕
(中南民族大学数学与统计学学院,武汉430074)
1 问题的引入
本文考虑下面一类具有扰动的向日葵方程:

其中a是分支参数,ε,μ,b是实的参数,并且0<ε≪1,r>0,b>0.ω=ω0(1-εη),η 为去谐参数.
先把方程(1)写成如下等价形式:

令t=sr,α(rs)=x(s),β(rs)=y(s),且仍记s=t,则有:

系统(3)又有如下等价形式:

系统(4)在v=0时,线性部分的特征方程是:

在文[1]中,已经讨论了系统(1)在v=0时的Hopf分支情况.文[1]中的结论是:当v=0时,系统(4)在μ=0时存在Hopf分支,且分支发生在μ<0方向,并且分支周期解是稳定的.在文[2]中,讨论了一类比较简单的扰动的向日葵方程的Hopf分支,得到了方程的调和解分支.本文将进一步考虑一类较复杂的扰动系统,即系统(4)在经历Hopf分支时,加上周期扰动所起的作用,即v≠0的情况.主要考虑周期扰动频率接近于σ0/2的情形,这里σ0是系统(4)的临界固有Hopf分支频率.
2 系统的简化

利用文[2]中的方法可以把系统简化.首先对系统(4)进行尺度变换,令,则(4) 式化为:再将变换后的系统写成滞后型泛函微分方程的形式.令C=C([-1,0],R2),L(εμ) 是C[-1,0]到R2上的有界线性算子族.于是由Riesz表示定理[3],存在一个二阶的、分量为有界变差函数的矩阵函数η(.,μ):[-1,0]→R2,使对任意φ∈C[-1,0],有.事实上,只要取

即可,其中 δ(θ) 是 Dirac δ-函数.
对 φ ∈C[-1,0],定义:

同时,由于对Ut=U(t+θ) ∈C[-1,0],有记U=(x,y)T于是系统(6)可写成:事实上,当θ=0时,(7)式就是(6)式[4].

令Λ={iσ0,-iσ0}是方程(5)的一对纯虚根,使用文[5]或文[6]的方法可以把方程(7)的解Ut分解到二维特征空间及其补空间上去,方程(7)可分解为:


3 次调和解的存在性与稳定性
下面讨论次调和共振情形下分支解的存在性与稳定性.对系统(8)的前2个方程施行积分平均法[6,7],可以揭示出该系统的扰动Hop f分支的性态.首先引入新的时间变量τ=ωt,则.再令u1(τ)=ξsin(Jτ+φ),u2(τ)=ξcos(Jτ+φ),其中J=σ0/ω0.在此变化下,忽略o(ε)项,系统(8)的前2个方程可化为:
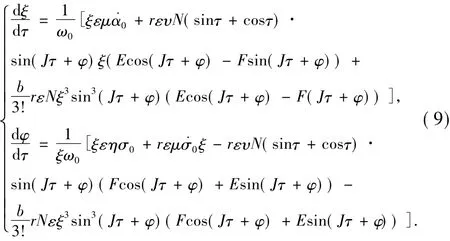
令J=1/2(二阶次调和共振情形),对方程(9)进行积分平均得到:
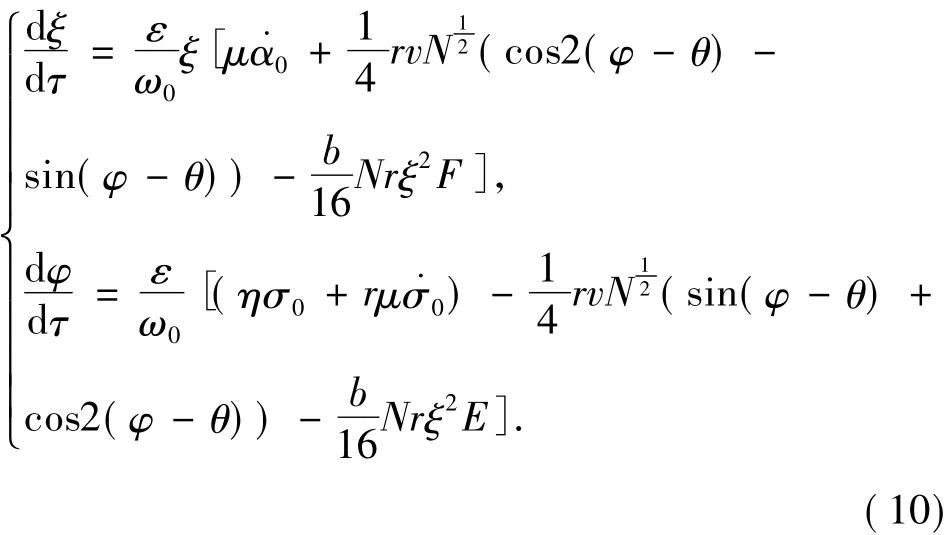
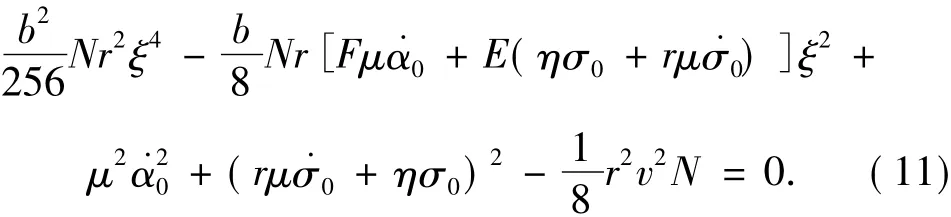
从方程(11)可看出其正根的分布情况:

方程(11)有2个正实根,从方程(11)中可求得:

现在考虑非平凡解的稳定性,令ξ=ξ0+υ1,φ=φ0+υ2,得到关于非平凡解的线性变分方程为:

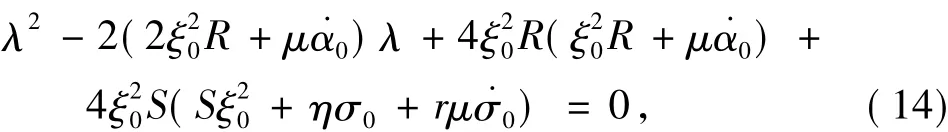
其特征根是:

因此,如果非平凡解满足条件

则非平凡解ξ0是稳定的,此时ξ0所对应的系统(1)的次调和分支解是稳定的.
容易看出由(12)式给出的较小的非平凡解始终不满足不等式(17),因此是不稳定的,而另一个解只要满足(16)式,则必是稳定的.
[1]魏俊杰.向日葵方程的Hopf分支[J].应用数学学报,1996,19(1):73-79.
[2]殷红燕,陈作清,胡智全.周期扰动对具有限时滞Lienard方程的Hopf分支的影响[J].华中师范大学学报:自然科学版,2010,44(3):361-364.
[3]Wiggins S.Introduce to applied nonlinear dynamical systems and chaos[M].Berlin:Springer-Verlag,1990:184-190.
[4]Namachivaya N S,Ariaratnam S T.Peridically pertured Hopf bifurcation[J].SIAM JAppl Math,1987,47(1):15-39.
[5]Hale J K.Theory of functional differential equations[M].Berlin:Springer-Verlag,1977:125-130.
[6]Kath W L.Resonance in periodical perturbed Hopf bifurcation[J].Studies in Applied Math,1981,65(1):95-112.
[7]Chow SN,Malled P.Integral averaging and bifurcation[J].JDifferential Equations,1977,26:112-159.
[8]岳锡亭,潘家齐.具有限时滞Van der pol方程的周期扰动 Hopf分支 [J].数学年刊,1992,13A(2):135-142.
