带有临界Sobolev指数和位势的拟线性方程的变号解

康东升，方 达，李智萍

(中南民族大学数学与统计学学院，武汉430074)

1 问题的引入

本文研究下列椭圆方程:

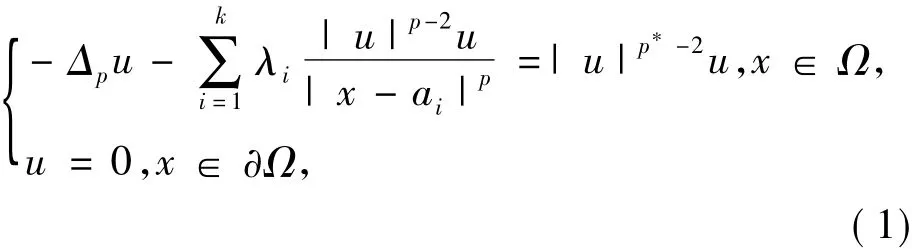
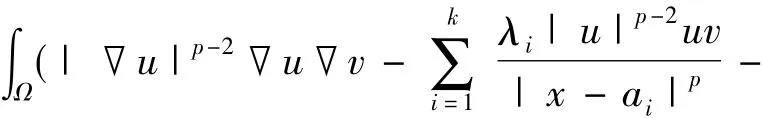
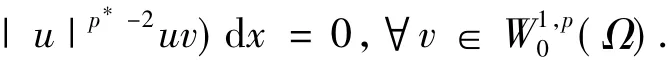
则称u为方程(1)的解.求方程(1)的解等价于求:

的临界点.

研究方程(1) 涉及到 Hardy 不等式［1，2］:

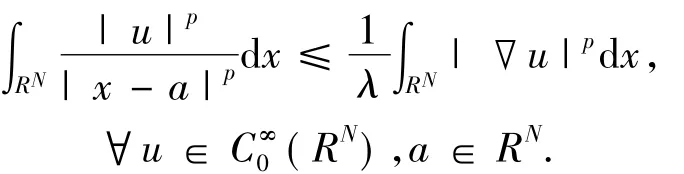
近年来，有作者研究含有Hardy项的椭圆极限问题:

文献［3］已经证明了当0＜λ＜¯λ和1＜p＜N时，方程(2)存在径向对称基态解:

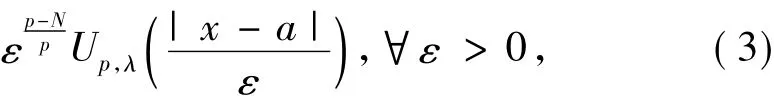
满足:

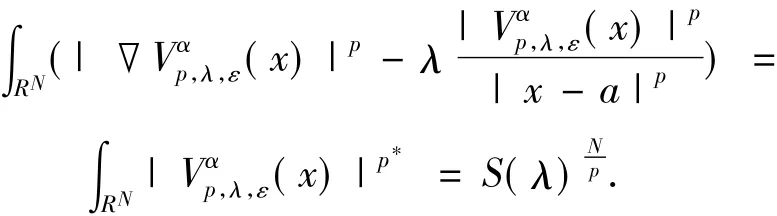
其中S(λ)是方程(2)对应的最佳 Sobolev常数，Up，λ(x)是方程(2)的径向解，满足:

其中C1，C2是关于 λ，p和N的正常数，a(λ) 和b(λ)是函数f(t)=(p－1)tp－(N－p)tp－1+λ(t≥0)的零点，满足:

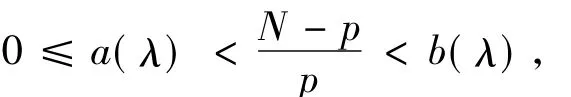
并且存在正常数L1(λ)和L2(λ)，使得:以上结果对于研究问题(1)非常重要.

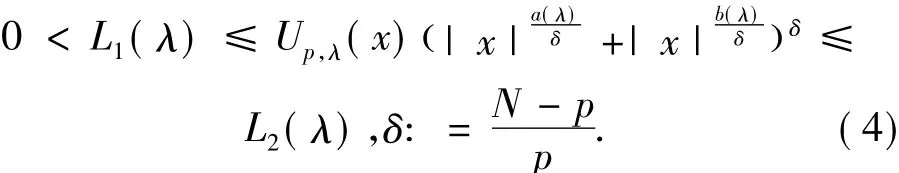
在本文中，我们假设:

(H1) λ1≤ λ2≤ … ≤ λk，k≥2，且存在l∈{0，1，2，…，k－1}，l0=0，使得:

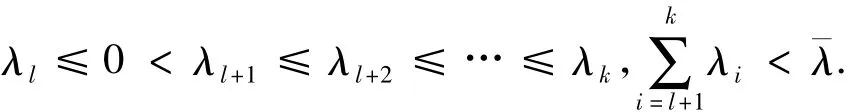
定义下列常数:

本文的主要结果如下.

定理1在假设(H1)下，如果下面2个条件之一成立:

(ii)2≤p＜N，N＞p(p2－p+1)，0＜λk＜λ＊＊且

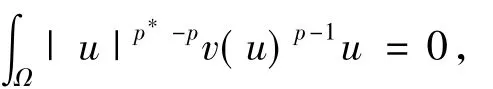
其中v(u)是加权特征值问题:

的第一本征函数.

在本文中，为简单起见，我们省略积分号中的“dx”.

2 变号解的存在性

为了研究方程(1)变号解的存在性，我们需要研究Mountain-Pass类型正解的奇性问题.

引理1存在v*＞0使得对任意的v∈(0，v*)，方程:

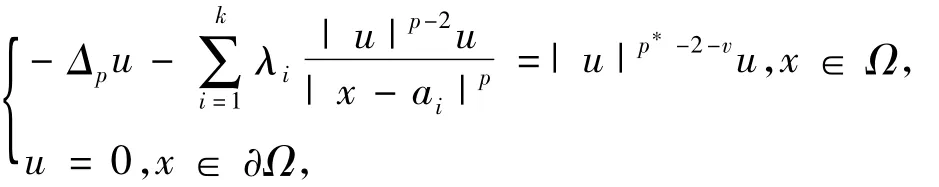
有变号解u2，v，使它满足:

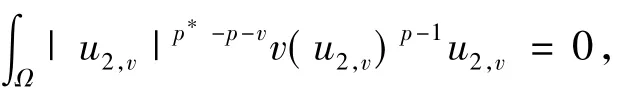
则v(u2，v)是加权特征值问题:

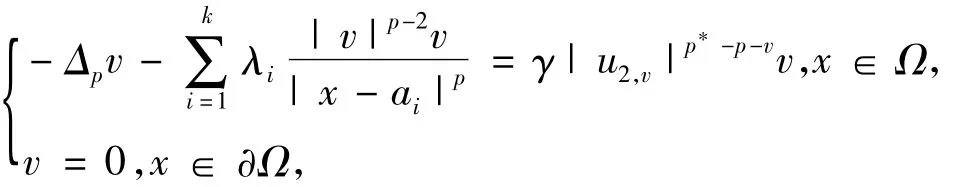
证明对v≥ 0，取v充分小且定义:当Jv∈C1(W1，p0(Ω)，R)，且对v'＞0，取v'充分小，则存在下界a0＞0使得:

则方程(1)就有一对变号解±u(x)满足:

由(6)～(9)式并结合文献［4］，引理1可得证.

引理2假设定理1，存在正常数σ，v＊＊满足:

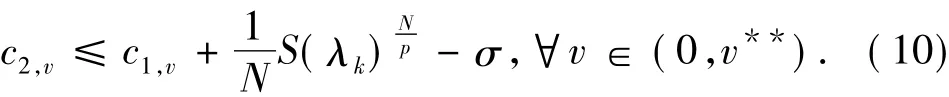
证明假设1＜p＜2，N＞N1，0＜λk＜λ*且，其中:

由文献［5］知，当N＞p(p+1)时，有:

注意到在这个假设下，有pb(λk)－N+p＞p，可得:

假 设p≥ 2，N＞N2，0＜λk＜λ＊＊且其中:

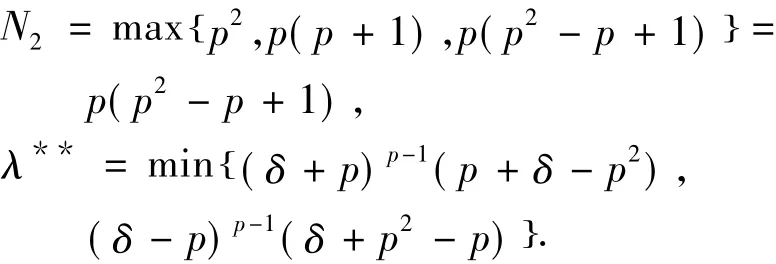
可得:

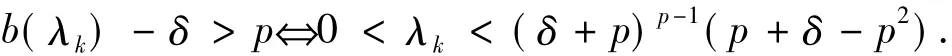
在这个假设中，同样有pb(λk)－N+p＞p，则:

因此，在定理1的假设下，方程(1)的Mountain-Pass类型正解u0∈W1，p0(Ω) 存在.根据文献［5］有对ε＞0，取ε充分小，则存在正常数C＞0满足:

对任意q∈［1，+∞)，存在常数C=C(q)＞0满足:

因此，由文献［6］中引理4的结论可以得到:

由上面估计可知，对ε＞0，取ε充分小，则有那么可以假定α和β在一个有界集中.由(11)式可得:

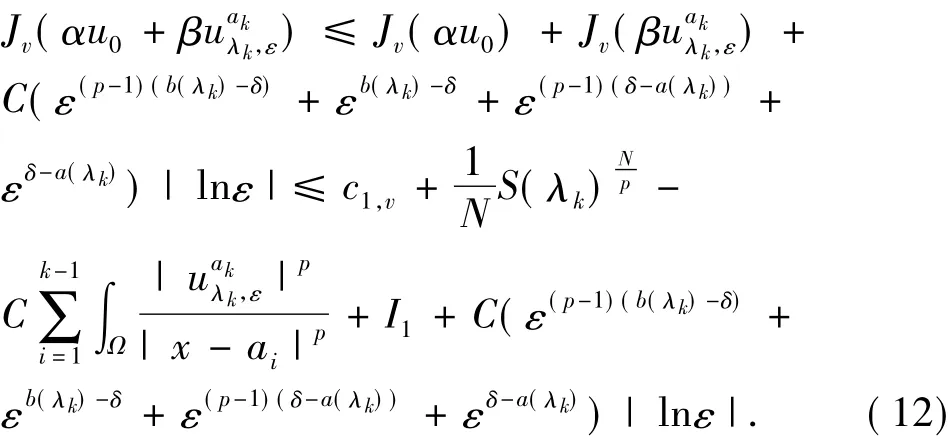
有:

往下我们分2种情况进行讨论.

(i)假设1＜p＜2，N＞N1，0＜λk＜λ*且.由(11)式可得:

当N＞p(p+1)时，有:

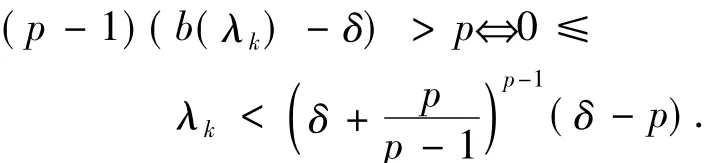
如果N(p－1)－2p2+p＞0，那么有＜δ，则:

如果N＞N1且0＜λk＜λ*，对ε＞0，取ε充分小，则存在常数σ＞0满足:

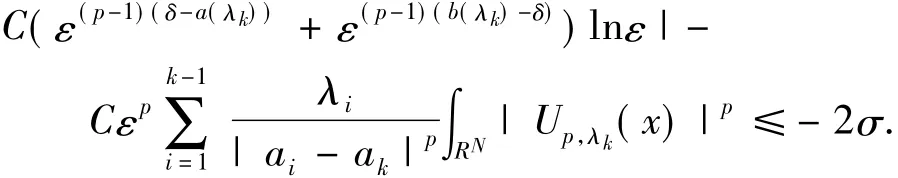
对v＊＊＞0，取v＊＊充分小，对0＜v＜v＊＊满足I1＜σ.然后由(13)式有:

(ii) 假设p≥2，N＞N2，0＜λk＜λ＊＊且，由(12)式可得:

注意当N＞p(p2－p+1)时:

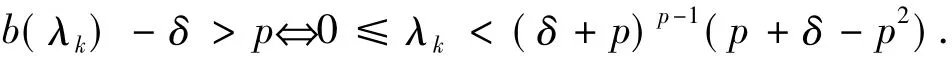
且当N＞p2+p时有:

如果N＞N2，0＜λk＜λ＊＊，ε 充分小，则有:

对常数σ＞0，取充分小的正数v＊＊，使得当0＜v＜v＊＊时，I1＜σ.则由(13)式和(14)式可得(10)式.

引理2证毕.

定理1的证明 证明过程类似于文献［4］和［7］.定义v0=min{v'，v*，V＊＊}.因为当v→0时，c1，v→c1，0，则由引理2 可得c2，v是均匀有界的，其中v∈(0，v0).假设c2，v是引理1的解，则存在常数C＞0满足:

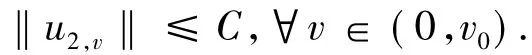
定义u±(x)={±u(x)，0}，对任意则可以发现对一些当vn→0时弱属于为了方便起见和 Λvn分别由un，

c1，n，c2，n，Jn和 Λn表示.因为则由引理2 可得:

当n充分大时，必然有:

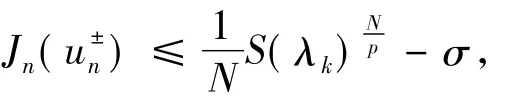
当n充分大.因为所以:

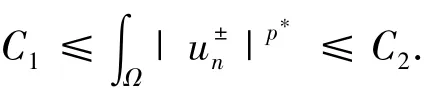
对正常数C1和C2，应用集中紧性原理［8，9］和文献［7］，可以得出在Ω中u±≠0.因此u在Ω内改变符号，un→u弱属于因此u是方程(1)的解.由n→ ∞，c2，n→c2，0容易证实{un} 实际上是J0在c2，0上的PS序列.事实上由再次应用集中紧性原理可以证明{un}的一个子序列在中强收敛于u.因此定理1证毕.

［1］Azorero J，Peral I.Hardy inequalities and some critical elliptic and parabolic problems［J］. J Differential Equations，1998，144(2):441-476.

［2］Hardy G，Littlewood J，Polya G.Inequalities［M］.Cambridge: Cambridge University Press，1988:239-243.

［3］Abdellaoui B，Felli V，Peral I.Existence and nonexistence for quasilinear equations involving thep-Laplacian［J］.Boll Unione Mat Ital Sez B，2006，9(2):445-484.

［4］Ghoussoub N，Yuan C.Multiple solutions for quasi-linear PDEs involving the critical Sobolev and Hardy exponents［J］.Trans Amer Math Soc，2000，352(2):5703-5743.

［5］康东升，李智萍，方 达.带有临界Sobolev指数和位势的拟线性方程的正解［J］.中南民族大学学报:自然科学版，2012，31(1):105-108.

［6］Kang D.Solutions for the quasilinear elliptic problems involving critical Hardy-Sobolev exponents［J］.Acta Mathematica Scientia，2010，30B(5):1529-1540.

［7］Cao D，Han P.Solutions to criticalelliptic equationswith multi-singular inverse square potentials［J］.JDifferential Equations，2006，224(2):332-372.

［8］Lions P L.The concentration compactness principle in the calculus of variations，the limit case(I) ［J］.Rev Mat Iberoamericana，1985，1(1):145-201.

［9］Lions P L.The concentration compactness principle in the calculus of variations，the limit case(II)［J］.Rev Mat Iberoamericana，1985，1(2):45-121.