用FPGA实现FIR数字滤波器的新方法

田莎莎，喻 成，汪 红

(中南民族大学计算机科学学院，武汉430074)

在图像处理、数据传输、雷达接收等现代信号处理领域，对信号处理的稳定性、实时性和灵活性都有很高的要求.有限冲激响应(FIR)数字滤波器因其线性相位特性满足了现代信号处理领域对滤波器的高性能要求，成为应用最广泛的数字滤波器之一.高密度的现场可编程门陈列(FPGA)兼顾实时性和灵活性，为FIR数字滤波器的实现提供了强大的硬件支持［1，2］.

用FPGA器件实现FIR数字滤波器硬件电路通常有2种实现方法:基于CSD编码的实现方法(简称为:CSD实现方法)和基于DA的实现方法(简称为:DA实现方法).用FPGA设计的FIR数字滤波器占用芯片面积的多少与滤波器系数有关，而针对不同滤波器系数分布情况，CSD和DA实现方法各有优缺点，为此本文提出了一种改进的实现方法:基于CSD-DA的改进实现方法(简称为:CSD-DA实现方法).仿真实验证明CSD-DA实现方法在一般情况下较前两种实现方法更加节约芯片面积.

1 FIR数字滤波器设计的理论依据

FIR数字滤波器的差分方程表达式［3］为:

式(1)中，n表示第n个单位时间(例如:0表示当前时间，1表示第1个单位时间)，N表示滤波器的阶数，h(m)表示第m个滤波器系数(共有N个滤波器系数，由于性能确定的FIR数字滤波器对应确定的一组系数，所以h(m)为一组常数)，x(n－m)表示第n－m个单位时间的采样输入，y(n)表示第n个单位时间的滤波器输出.

令h(n)表示第n个滤波器系数，x(n)表示第n个时间之前的采样输入，y表示当前时间的滤波器输出，式(1)可变为:

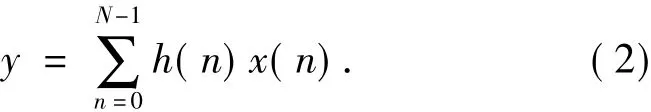
由于线性相位的FIR数字滤波器满足滤波系数的对称性［3，4］，因此当N为偶数时，式(2) 可以表示为:

由式(3)可知，输入采样值x(n)和x(N－1－n)先进行相加再与对称系数相乘，若设d(n)=x(n)+x(N－1－n)，则式(3)可表示为:

当N为奇数时，式(2)可以表示为:

对式(5)，当0≤n＜(N－1)/2，设d(n)=x(n)+x(N－1－n);当n=(N－1)/2时，如果设

则式(5)可以表示为:

将式(4)，式(6) 统一为［5］:

在式(7)中，当滤波器阶数N为偶数时，s=N/2;N为奇数时，s=(N+1)/2.

对于FIR滤波运算中x(n)的延时操作和d(n)=x(n)+x(N－1－n)的加法操作，其运算速度是由输入序列的采样频率决定的，芯片占用面积是由滤波器的阶数决定的，很难进行优化，但式(7)中的“乘积和模块”却有很大的优化空间.根据式(7)，可画出FIR数字滤波器的“乘积和模块”电路框图，如图1所示.

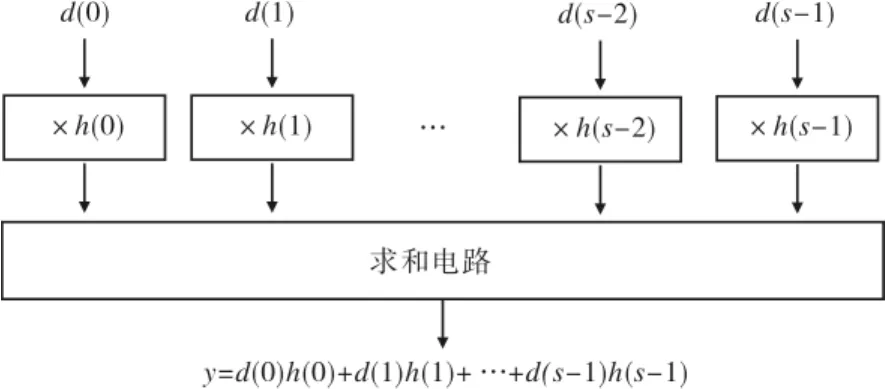
图1 “乘积和模块”电路框图Fig.1 “Summing aftermultipling”circuit scheme chart

2 FIR数字滤波器的实现方法

2.1 CSD 实现方法

CSD编码是数字信号处理中设计常系数乘法器时常用的一种编码方式.最佳CSD编码算法可以描述为［1］:

表1 8位二进制整数对应的C值Tab.1 Corresponding C of8 bit binary integer

2)从最高有效位开始，用011代替10

CSD实现方法是将图1中h(n)的数值部分用CSD编码表示，在乘积项求和时再将系数的符号考虑进去.h(n)的CSD编码中1和的个数减去1即为此常系数乘法所需加法器的数目.从表1［1］可以查到8位二进制整数作为常数因子时用移位-加法器实现常系数乘法时所需的加法器个数C.例如h(n)为255时，其CSD编码为1000000，从表1中可以查到所需加法器数目C为1，255·d(n)的运算是将d(n)左移8位后再和d(n)相加减.

2.2 DA 实现方法

FPGA内部大量的查找表(Look-up Tables，LUT)资源结合DA可以巧妙地实现FIR数字滤波器中的“乘积和模块”.DA算法是将式(2)变换为式(8)的形式［1］，式(8)中xb(n)表示第n个数据的第b位，因为h(n)已知，所以可利用查找表通过查表方法实现f(h(n)，xb(n))，再通过相应的二次幂加权并累加得到y:

设计FIR数字滤波器时，要减少对FPGA芯片面积的占用，降低硬件成本，就要减小LUT的规模，国内外的相关文献提出了多种方法.有些采用OBC编码方式，有些采用多路选择器来减小查找表规模.文献［6］则论证了表分割方法较其它方法在减小查找表规模上性能更优.表分割是将一个大的查找表分成多个小的查找表.假设将一个N输入的大查找表分割成R个小查找表，R个小查找表的输入个数分别为N1，N2，…，NR，其中N=N1+N2+…+NR，则式(2)可变为:

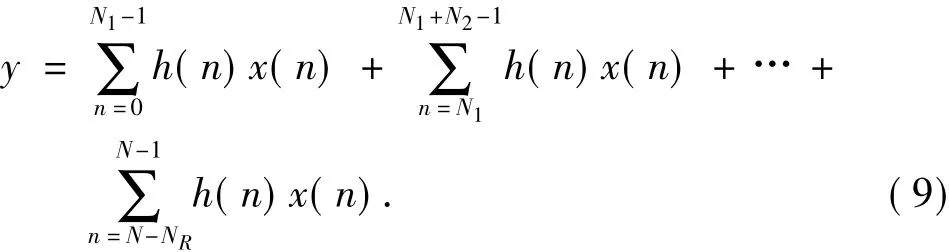
令X(n)=h(n)x(n)，假设X(n)共有B位二进制位，由式(9)可得表分割DA算法的电路原理框图，见图2.

3 CSD-DA实现方法的原理及实验验证

图2 表分割电路原理框图Fig.2 Principle scheme chart of cutting table circuit

3.1 CSD-DA 实现方法

文献［6］提出了用表分割的DA算法实现FIR数字滤波器的思想，文献［7］提出了CSD实现方法实现FIR数字滤波器中的常系数乘法器的思想，文献［8］把CSD和DA实现方法实现FIR数字滤波器的占用硬件资源情况进行了对比，得到了这样的结论:从资源利用的角度来讲，在一般情况下，CSD实现方法占用资源较少，但是最坏情况下还是DA算法占用芯片面积少.通过这些文献可以得到这样的结论:DA和CSD实现方法实现FIR数字滤波器时在占用硬件资源方面各有优缺点.

由于DA实现方法设计的FIR数字滤波器，其运算速度只与输入采样值的位数有关，与滤波器阶数无关，其运算速度不会随着滤波器阶数的增加而降低.另外查找表的HDL语言程序可以借助可执行程序快速生成，且更改设计简单.而CSD实现方法在设计多个不同的乘法器时，实现方法较为复杂.所以当占用硬件资源几乎一样的情况下，用DA实现方法较CSD实现方法设计FIR数字滤波器简单方便［1］.

为了将CSD与DA实现方法进行更好的比较，在FPGA芯片Cyclone EPEC6Q240C8上进行了一组实验.表2给出了实验中CSD和DA实现方法实现的几个典型系数FIR数字滤波器所需的逻辑元件(Logic element，LE)数目，一个LE包括一个LUT和一个D触发器.

表2的实验结果表明2种实现方法各有优劣.在滤波器系数对应的C值为0或1时CSD实现方法优势明显;滤波器系数对应的C值为3或4时DA实现方法优势明显;滤波器系数对应C值都为2时二者差别不大，但由于DA实现方法较为简单，此时DA实现方法更有优势.

根据上面的实验结果与理论分析，可以总结出改进的CSD-DA实现方法:将图1中的“乘积和模块”分成2个子模块，一个子模块用CSD实现方法实现系数对应的C值为0，1的“乘积和”，另一个子模块用DA实现方法实现系数对应的C值为2，3，4时的“乘积和”，最后将2个子模块的结果相加.

表2 DA与CSD实现方法占用LE比较Tab.2 LE occupation comparison between DA and CSD implementation method

3.2 CSD-DA实现方法的实验验证

为了验证CSD-DA实现方法在一定情况下较DA和CSD实现方法优越，在Cyclone EPEC6Q240C8芯片上实现了多个FIR数字滤波器，并从中选取了4个FIR滤波器占用的LE数目和滤波系数对应的C值列于表3.从表3的实验结果可以看出:当滤波器各系数对应的C值几乎都是0，1时CSD实现方法最优;当滤波器各系数对应的C值大部分都是2，3，4时DA实现方法最优;其余情况CSD-DA实现方法最优.而在一般情况下，滤波器各系数对应的C值比较分散，不会都集中在0、1或2、3、4，所以在一般情况下CSD-DA实现方法较DA和CSD实现方法占用的芯片面积少.

表3 3种实现方法实现4个实例的实验结果Tab.3 Experimental results of four examples by using three implementation methods

为了系统的验证CSD-DA实现方法，本文用CSD-DA实现方法在Cyclone EPEC6Q240C8芯片和音频编解码芯片TLV320AIC23B上成功实现了一个可以滤除音频信号中高频噪声的FIR数字低通滤波器［9，10］，如图 3 为此 FIR 滤波器的 Quartus2 仿真时序图，图4为MATLAB软件计算滤波输出的结果，比较两图可知结果完全一致，因此滤波器的硬件设计是成功的.

图3 FIR低通滤波器时序仿真图Fig.3 Timing simulation chart of the FIR low-pass filter

图4 FIR低通滤波器MATLAB计算结果Fig.4 MATLAB calculation results of the FIR low-pass filter

4 结语

FIR数字滤波器是数字信号处理电路中的重要部件，本文提出的CSD-DA实现方法丰富了FIR数字滤波器的设计方案体系.在一般情况下这种改进的实现方法比现今常用的CSD和DA实现方法更加节约芯片面积.仿真实验结果表明CSD-DA实现方法实现的FIR数字滤波器性能良好，节省硬件资源，能满足实际数字系统的需要.

［1］Uwe M B.数字信号处理的FPGA实现［M］.刘 凌，译.北京:清华大学出版社，2006:1-123.

［2］王文涛，王 建，朱顺安.基于FPGA的女书文字切割技术的设计与应用［J］.中南民族大学学报:自然科学版，2011，30(1):96-100.

［3］程佩青.数字信号处理教程［M］.北京:清华大学出版社，2001:202-226，334-388.

［4］Tsao Y C，Choi K.Area-efficient parallel FIR digital filter structures for symmetric convolution based on fast FIR algorithm［J］.IEEE Transaction on VLSI Systems，2010(99):1-5.

［5］Chen He，Xiong Chenghuan，Zhong Shunan.FPGA-based efficient programmable polyphase FIR Filter［J］.Journal of Beijing Institute of Technology，2005，14(1):4-8.

［6］Meher P K，Chandrasekaran S，Amira A.FPGA realization of FIR filters by efficient and flexible systemization using distributed arithmetic［J］.IEEE Transactions on Signal Processing，2008，56(7):3009-3017.

［7］李 京，沈 泊.一种低功耗常系数乘法器的设计［J］.计算机工程与应用，2005，41(30):99-101.

［8］朱 霞，柴志雷，须文波.基于CSD编码的FIR数字滤波器优化设计［J］.计算机工程与设计，2009，30(2):271-274.

［9］王 诚，吴继华，范丽珍，等.Altera FPGA/CPLD设计基础篇［M］.北京:人民邮电出版社，2005:1-170.

［10］王 诚，吴继华，范丽珍，等.Altera FPGA/CPLD设计高级篇［M］.北京:人民邮电出版社，2005:1-96.