对FD-DB-Ⅱ型单摆实验仪功能的拓展
2012-02-01潘友华陆法林
潘友华,陆法林,陈 峰
(盐城师范学院物理科学与电子技术学院,江苏盐城224051)
1 引 言
单摆实验在大学基础物理实验中是一个重要的必做实验,对此实验的研究也较多[1-5].我们实验室使用的上海复旦天欣科教仪器有限公司FDDB-Ⅱ型单摆实验仪,采用集成开关型霍尔传感器和电子计时器实现自动计时,能够在较少的几个振动周期内,精确地测得角振幅θ0(最大摆角)很小时的单摆周期,有效减少了计时误差,从而能比较精确地测得重力加速度.在使用该仪器的过程中发现,仪器的功能还可以进一步拓展,在该实验仪上增加了很少的几个配件,结果表明:除可使仪器操作更加方便、实验结果更加准确外,还能定量研究周期T与θ0的关系.
2 对装置的改进
改进后的装置如图1所示,主要添加了2个配件:
1)可计算角振幅的刻度板
如图2所示,刻度板是背面贴上薄平面镜的刻度尺,将刻度板水平固定在支架上,并可沿支架上下位置任意调整,这样可较为准确地读出小球在角振幅位置时摆线(摆线上端点到刻度尺上边的垂直距离为Y)的水平位移X,然后可以根据tanθ=X/Y得出单摆的角振幅θ0.
2)电磁铁控制摆球的释放

图1 改进后的装置

图2 刻度板的构造
自制电磁铁如图3所示,通电时该电磁铁能吸住1个铁质摆球.电磁铁通过控制开关与电源相接,通电时摆球被吸住,断电时摆球由静止开始作自由摆动.将电磁铁固定于特制的支架内,通过此支架可以任意调整电磁铁的位置,支架可沿刻度板移动,应保证电磁铁的中心在摆球运动的平面内.

图3 电磁铁的构造图
3 实验内容的拓展
主要从周期与角振幅的关系和测重力加速度两方面作一些探讨.
3.1 周期与角振幅
以往单摆测重力加速度实验都局限在单摆在小角度(小于5°)内做近似等周期摆动的情况下,测量单摆周期,一般不涉及周期与角振幅之间的关系.小角度单摆的振动周期为T0=2π,由于摆长l与g没有变化,因此小角度单摆的振动周期是常量,与角振幅θ0无关.
单摆的实际振动周期为[5]

略去高阶项,取一级近似有:

θ0很小时,取零级近似有:T=T0=2π.根据式(2)描绘的T/T0-θ0关系的理论曲线见图4.从图4可以看出,单摆的周期与角振幅有关,周期随角振幅的增大而增大,不是线性关系.
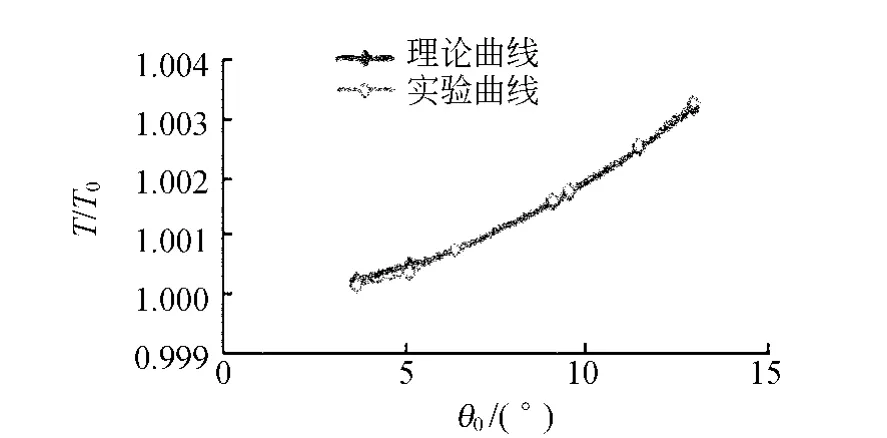
图4 实验曲线
以特定摆长下的角振幅与周期关系为例,不考虑空气阻力、摆线与悬挂点之间的摩擦力等因素,取摆线长度L1=(75.60±0.05)cm,摆球半径L2=(1.013±0.001)cm,摆长为:L=L1+L2=(76.61±0.05)cm,盐城气象局提供的当地重力加速度值为g=9.795 9m·s-2,由此可得T0=1.757 1s.
角振幅可先测得X和Y,再由tanθ0=X/Y求得.实验中测得不同角振幅下的周期,结果见表1(取Y=0.720 0m).
表1 周期与角振幅、的关系

表1 周期与角振幅、的关系
X/mθ0/(°)sin2θ0 T/s平均值0.046 5 3.70 0.001 040 1.758 1.758 1.758 1.758 1 21 2 3 4 5 6 7 8 9.758 1.756 1.758 1.756 1.757 1.757 4 0.080 5 6.38 0.003 096 1.758 1.758 1.758 1.759 1.759 1.759 1.758 1.759 1.758 1.758 4 0.114 5 9.04 0.006 205 1.760 1.760 1.760 1.760 1.759 1.760 1.760 1.760 1.760 1.759 9 0.120 5 9.50 0.006 859 1.760 1.759 1.760 1.761 1.760 1.760 1.760 1.761 1.761 1.760 2 0.145 5 11.42 0.009 907 1.761 1.762 1.761 1.762 1.762 1.760 1.762 1.762 1.762 1.761 6 0.165 5 12.95 0.012 708 1.763 1.762 1.763 1.7631.762 1.763 1.763 1.763 1.763 1.762 8
从图4可以看出,随着θ0增大T/T0逐渐增大,T/T0与θ0曲线的斜率也逐渐变大.实验曲线与理论曲线基本吻合,验证了单摆在角振幅较大时T/T0与θ0成非线性关系.
3.2 用单摆测重力加速度
用传统的手控计时方法,单次测量周期的误差可达0.1~0.2s,而多次测量又面临空气阻力使摆角衰减的情况,因而(2)式只能考虑到零级近似,而忽略.但是,当单摆振动周期可以精确测量时,可以考虑摆角对周期的影响,即可用一级近似公式.在此实验中,测出不同的θ0所对应的周期T,利用Excel绘出曲线,如图5所示,并将其外推,从截距得到单摆周期,从而更精确地测得重力加速度g.同时可得:相关系数r=0.994 5,截距A=1.757 0s,此即周期T.将T=1.757 0s和θ0=0代入(4)式,计算得到:g=9.797 5m·s-2,该值与盐城当地重力加速度的公认值很接近,实验结果的相对偏差仅为0.016%.

图5 曲线
4 结束语
改进后的单摆实验仪可以通过刻度板计算出角振幅θ0,从而能定量研究周期T与角振幅θ0的关系.在测量重力加速度时,用曲线外推,从截距A得到周期T数据的处理方法得到更为精确的结果.电磁铁的添加保证了摆球运动的初速度为0,提高了小球做单摆运动的成功率,也增强了整个实验装置的可操作性.可保证摆球在一段时间内做单摆运动.
[1] 鞠衍清.任意摆角单摆运动周期的一个近似公式[J].沈阳工业大学学报,2006,28(2):230-232.
[2] 韦德泉,王秋芳.单摆的角振幅对其周期的影响[J].洛阳大学学报,2003,18(2):102-103.
[3] 夏清华,杨国海.两例非线性振动周期的计算[J].高等函授学报(自然科学版),1999(4):28-30.
[4] 赵继红.单摆实验数据处理[J].太原师范专科学校学报,2001(3):12-13.
[5] 杨述武,马葭生,贾玉民,等.普通物理实验(力学及热学部分)[M].3版.北京:高等教育出版社,2004:69-73.
