非理想载波同步下的OFDM快衰落信道估计
2012-01-31赵维杰
方 勇, 赵维杰, 汪 敏
(上海大学特种光纤与光接入网省部共建重点实验室,上海200072)
OFDM技术以其高效的频谱利用率而被LTE (long term evolution)和802.16m等下一代移动通信标准所选用.OFDM系统对非理想载波同步引起的载波频率偏移(carrier frequency offset,CFO)和高速移动引起的快衰落信道都十分敏感,二者均会破坏子载波间的正交性并引起子载波间干扰(intercarrier interference,ICI),从而导致误码率(BER)性能下降[1].为了克服非理想载波同步问题,必须采用ICI消除技术[2],而针对快衰落信道,则需要使用快衰落信道估计技术[3].但是,ICI消除技术只对理想信道有效,即该技术必须在信道估计及均衡之后完成;而现有的信道估计算法却依赖于精确的载波同步,也就是说信道估计必须在ICI消除技术应用之后才能生效,二者相互矛盾.所以,为了解决这一矛盾,研究非理想同步下的快衰落信道估计技术有重要意义.
目前,针对非理想载波同步问题,有3类ICI消除算法,分别是ICI自消除[6-8]、频域均衡[4]以及时域加窗[5].这3类算法均假设无线信道的频率响应是已知的并且等于1,这意味着在使用ICI消除技术之前必须对快衰落信道进行快衰落信道估计及均衡.现有的快衰落信道估计算法利用已知的快衰落信道的统计特性,在时域或变换域中减少待估计的参数个数,使导频方程成为超定的,再利用LS或者最小均方误差(minimum mean squared error,MMSE)估计器进行信道估计[3,9-16].文献[3]在时域中利用已知的信道抽头间最大后验(maximum a posteriori,MAP)概率的方法来减少待估计参数个数;文献[9]提出了基于基扩展模型(basis expansion model,BEM)的快衰落信道估计方法,该方法利用信道在频域中的稀疏性来减少待估计参数个数,该稀疏性源于信道功率谱密度所具有的低通特性;同样,文献[10-11]提出的广义复指数基扩展模型(general complex-exponential-BEM,GCE-BEM)算法,以及文献[12]提出的多项式基扩展模型(polynomial-BEM,P-BEM)算法等都属于BEM类算法,只是每个算法所利用的变换域不同.可见,现有的快衰落信道估计算法中,待估计参数的减少必须依赖于已知的信道统计特性,这是唯一已知的先验知识.但在非理想载波同步时,信道的自相关矩阵由于受到CFO的影响变为一个未知的随机矩阵,那么这些使参数减少的方法便会失效,从而无法完成非理想载波同步下的快衰落信道估计.另一方面,这些算法都将非导频项归入高斯噪声项中,增大了建模误差,降低了估计精度.
为此,本研究提出一种非理想载波同步下的快衰落信道估计算法,该算法可以同时克服CFO和快衰落信道产生的ICI.首先,将CFO与快衰落CIR矩阵结合,提出了广义信道冲击响应矩阵(G-CIR),建立了非理想同步快衰落信道估计模型;然后,利用G-CIR自相关矩阵的统计特性,提出了G-CIR自相关矩阵的对角化方法,并由此推导出了基于信道核向量的紧凑型CIR矩阵压缩表示及其等效信道模型,减少了待估计参数个数,降低了建模误差;最后,利用最小二乘(LS)估计器估计出信道核向量,并重构出快衰落CIR矩阵.仿真结果验证了本研究提出的非理想载波同步下快衰落信道估计算法的有效性.
1 系统模型
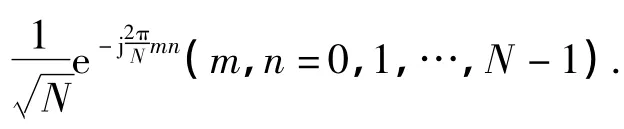
在非理想载波同步下,n时刻第k个子载波上的解调信号Y(k)可以表示为
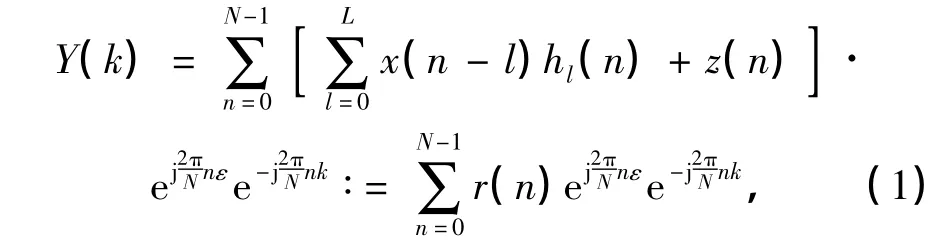
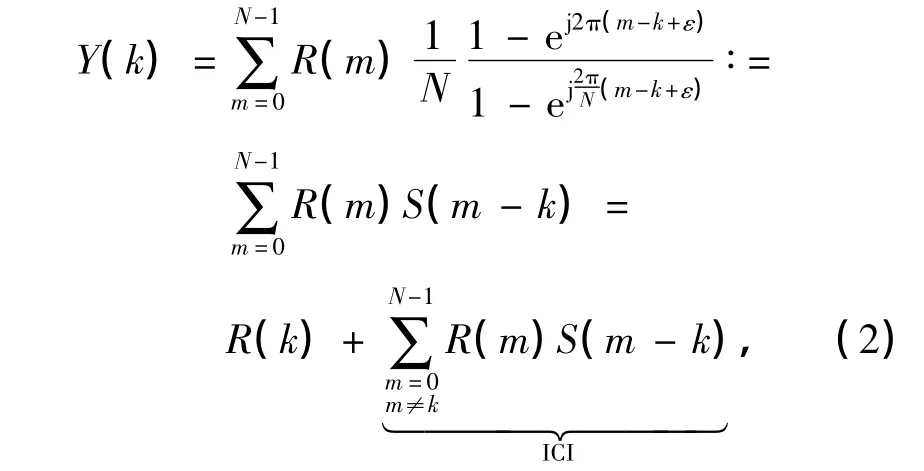


式中,r=[r(0),r(1),…,r(N-1)]T为时域接收信号向量,z=[z(0),z(1),…,z(N-1)]T为时域加性高斯白噪声(additive white Gaussion noise,AWGN)向量,H为信道冲击响应(CIR)矩阵.假设最大可辨多径数为L,则H可以表示为
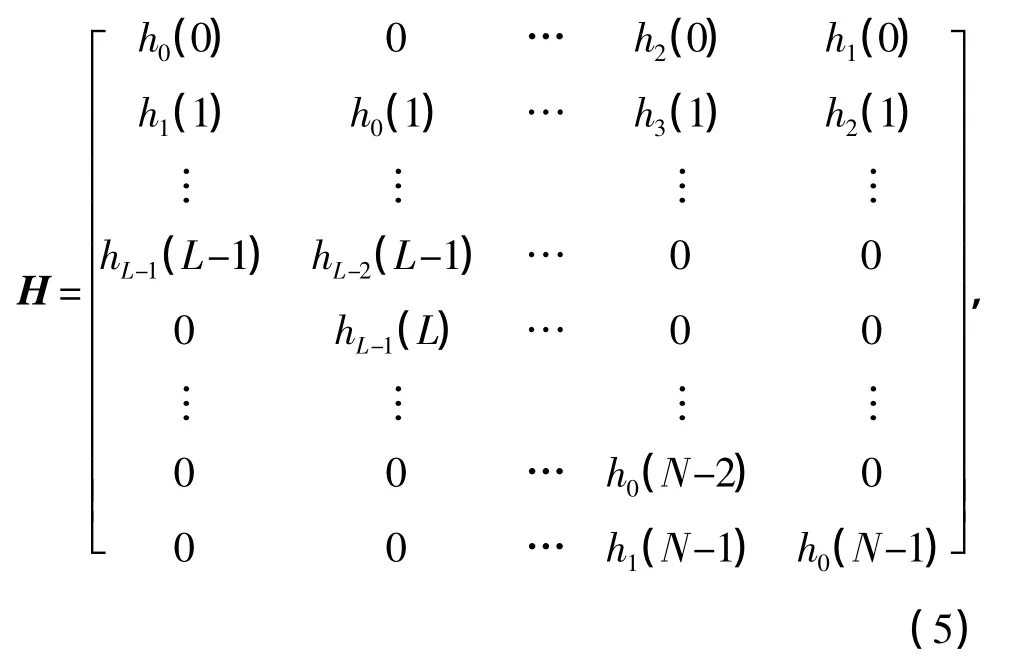
式中,hl(n)为n接收时刻第l(0≤l≤L-1)条径上的信道冲击响应系数,它是一个零均值的复高斯过程.根据Jakes模型,hl(n)的自相关函数满足[8]
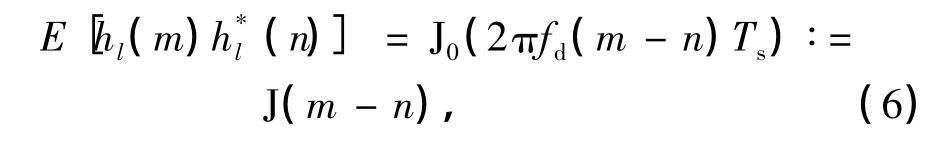
式中,J0(·)表示第一类零阶贝塞尔函数,fd和Ts分别表示最大多普勒频移和采样时间.对式(4)两边进行快速傅里叶变换(FFT),得到如下频域信道模型:
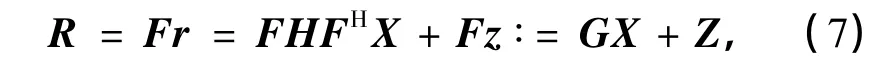
式中,G∶=FHFH为信道传输矩阵,Z为频域噪声向量.在快衰落情况下,G是一个带型矩阵,其矩阵带宽与fd有关.将式(7)代入式(3),可以得到非理想同步时的频域通用信道模型如下:
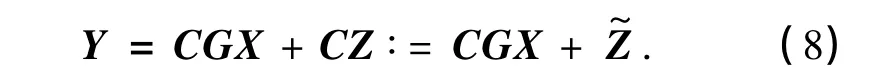
根据循环矩阵的性质,可以用FFT矩阵F对C进行奇异值分解 C=FΛFH,其中 Λ=diag(λ0,λ1,…,λN-1)为对角阵,其第i个元素λi可以表示为C的第一行元素的DFT变换,因此,
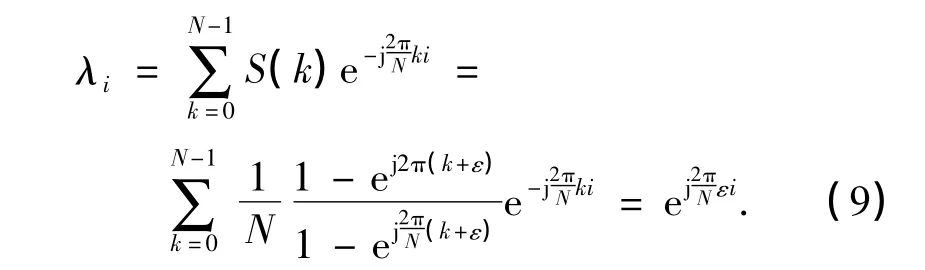
利用C的奇异值分解,可以将式(8)重写为
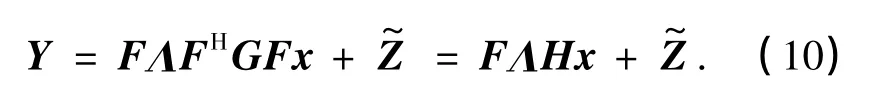
对式(10)进行IFFT变换,可以得到非理想同步时的时域通用信道模型:
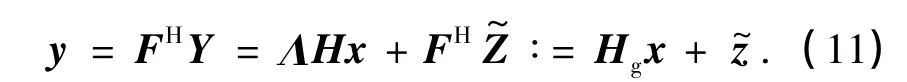
定义Hg∶=ΛH为G-CIR矩阵,它同时包含了CFO和快衰落信道两种信息.由此,建立了非理想载波同步下的快衰落信道模型,并将对实际信道的估计转化为对Hg的估计.特别地,在理想同步下,矩阵Λ退化为单位阵,此时,问题简化为传统的快衰落信道估计问题.而在非理想同步下,频域上G与C相乘后不再是带型矩阵,这不仅使未知元素增多为N×N个,而且带来了更加严重的ICI;时域上对角阵Λ与H相乘后虽然没有使未知元素个数增多(仍为N× L个),但却改变了H的统计特性,使其自相关不再满足式(6),即Hg的自相关矩阵是一个未知矩阵.另外,无论是在时域还是频域上,信道未知元素个数均数倍于子载波个数N,也就是说,即使插满导频也只能得到一个欠定方程组.因此,必须对Hg的自相关矩阵进行研究,并在此基础上提出信道的压缩表示方法,以减少待估计参数的个数,从而完成非理想载波同步下的信道估计.
2 紧凑型G-CIR自相关矩阵的对角化方法
下面将对G-CIR自相关矩阵的统计特性进行研究,并提出紧凑型G-CIR自相关矩阵的对角化方法.该方法将自相关矩阵的随机性约束在对角阵中,为信道压缩表示提供基础.
2.1 紧凑型G-CIR矩阵及其统计特性
为了简化问题,先将实际CIR矩阵H中的0元素去除,定义紧凑型CIR矩阵为
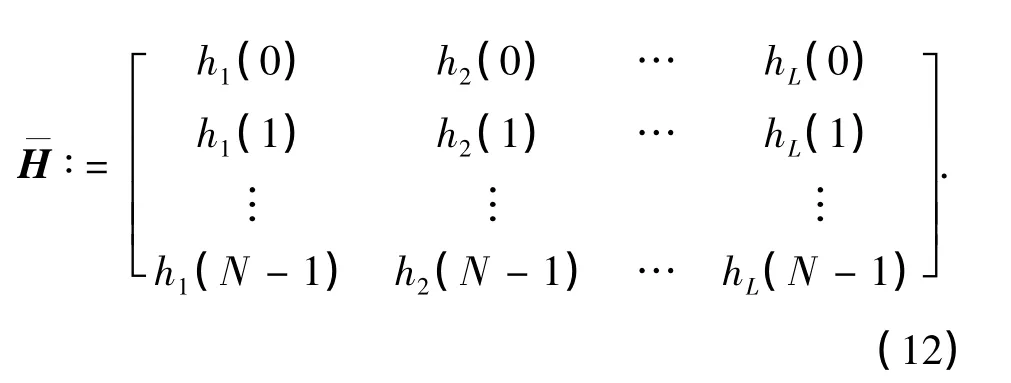

由于在接收机完成同步操作后,频偏ε是个未知的确定值,所以矩阵Λ在每次接收时也是个未知的确定矩阵.那么,根据式(6)和(13),可以计算出紧凑型G-CIR自相关矩阵
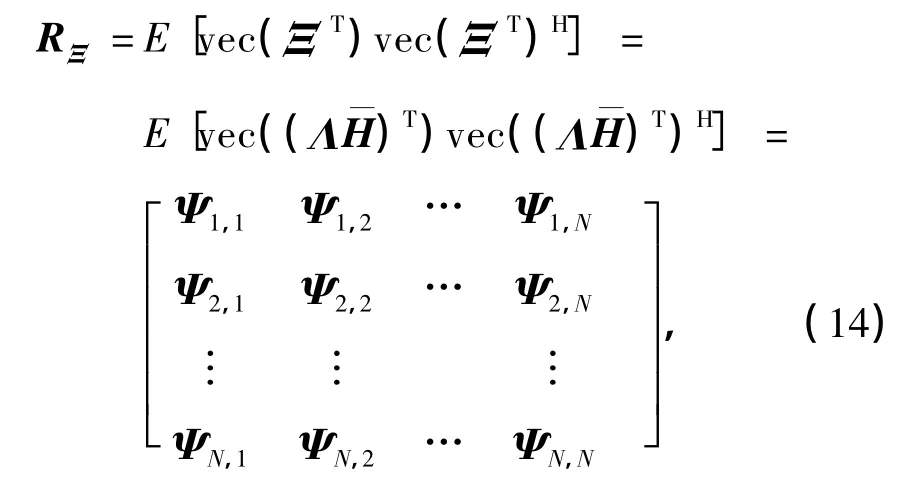
式中,
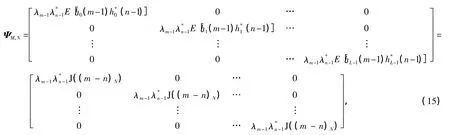
式中,(·)N表示模N运算.利用Kronecker积的性质[17],可以将式(14)重写为
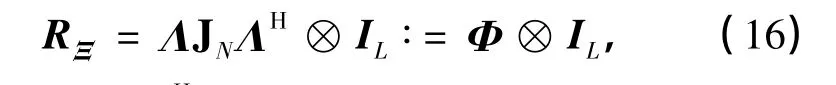
式中,Φ∶=ΛJNΛH,
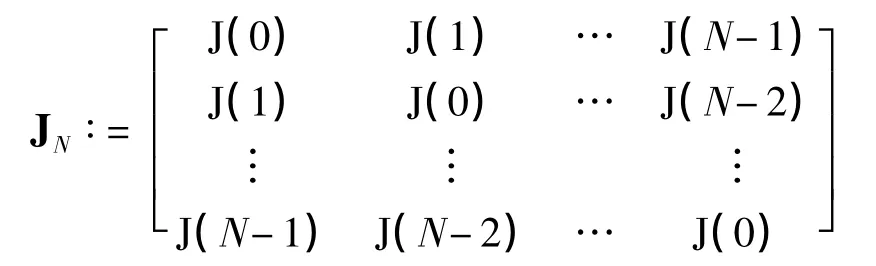
为第一类零阶贝塞尔矩阵,IL为L×L的单位阵,⊗表示Kronecker积.根据Hadamard积的性质[17],可将Φ写成Φ=(ΛΛH)⊙JN,其中⊙表示Hadamard积.根据式(9),可将ΛΛH化简得
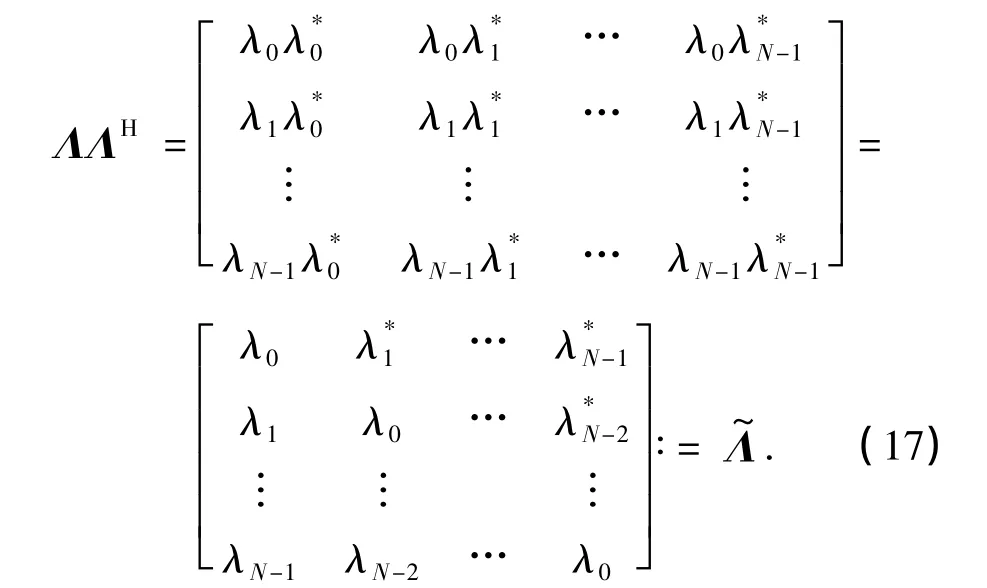
于是,Φ可以进一步化简为
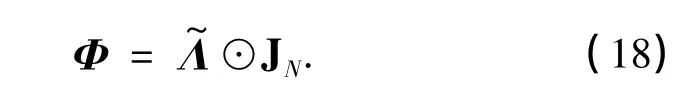
2.2 紧凑型G-CIR自相关矩阵的对角化表示
下面研究紧凑型G-CIR自相关矩阵的对角化表示方法,将RΞ分解为2个确定的酉阵和一个随机的对角阵的乘积,使RΞ的随机性仅体现在对角阵中.由于RΞ的随机部分仅由Φ决定,所以先考察Φ.为了分离Φ中的随机部分,利用向量化算子[17]vec(·)对Φ进行向量化操作
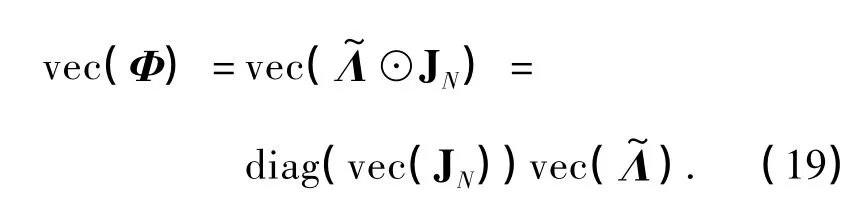
定义函数f(m)=(m-1)mod N和g(m)=「m/N⏋-1用于计算向量化前后的元素下标,则vec()中第m个元素为(f(m),g(m)).定义vec()的自相关矩阵R为
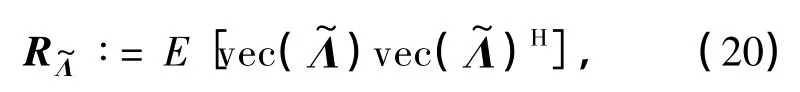
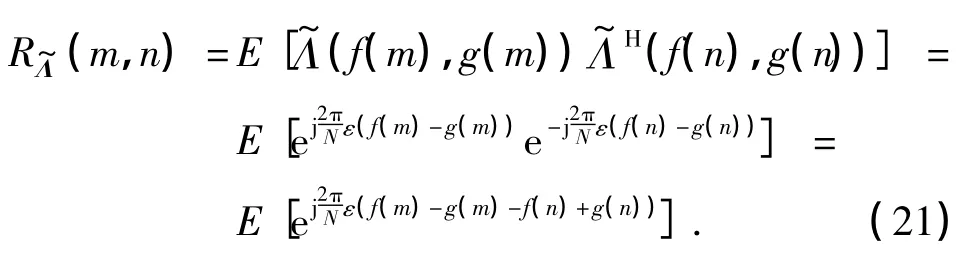
假设对归一化频偏ε的统计特性一无所知,那么ε为[0,1]上均匀分布的随机变量,因此,

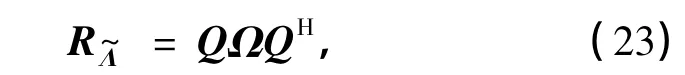
式中,Q为NN×NN的酉阵,Ω为NN×NN的对角阵.由于Q是酉阵,那么其NN个列向量是NN维向量空间的一组标准正交基,因此,NN维列向量vec()可以由以下这组基线性表示:
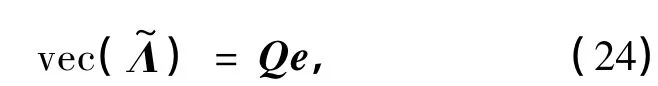
式中,e为NN维随机列向量,其均方为E[eeH]= Ω,这可以由下式来证明:
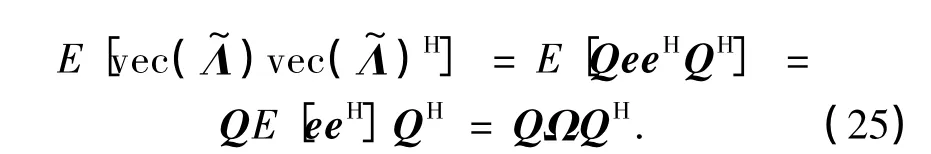
如果将e中均方值较小的元素作为建模误差并去除,则可以减少e的维数.由于e的均方由Ω的奇异值决定,因此,保留Ω对角线上前M大的元素并记为Ω(t),那么=Q(t)Ω(t)Q(t)H,其中Q(t)由Ω中被保留的奇异值在Q中的对应列组成.由此,式(24)可以近似写成
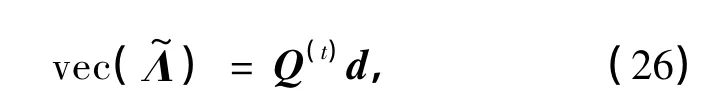
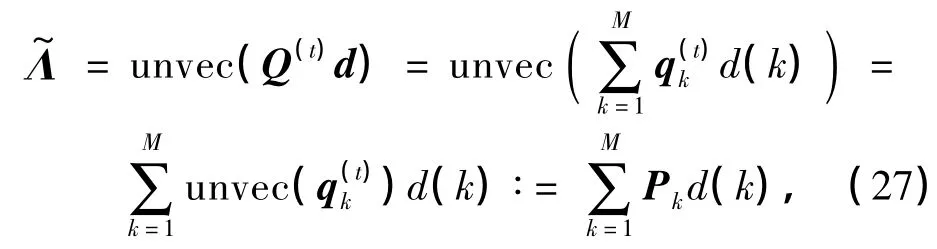
式中,Pk∶=unvec()为矩阵化后的N×N维矩阵.将式(27)代入式(18),可得
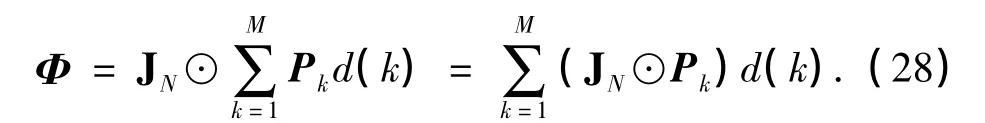
对 JN⊙Pk进行奇异值分解,可得 JN⊙Pk= UkΔkVHk,则
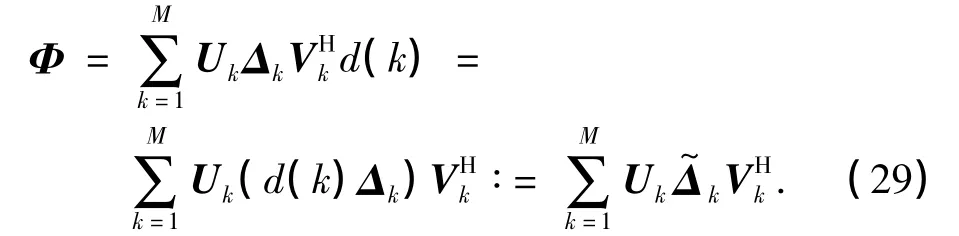
将式(29)写成矩阵形式,可得
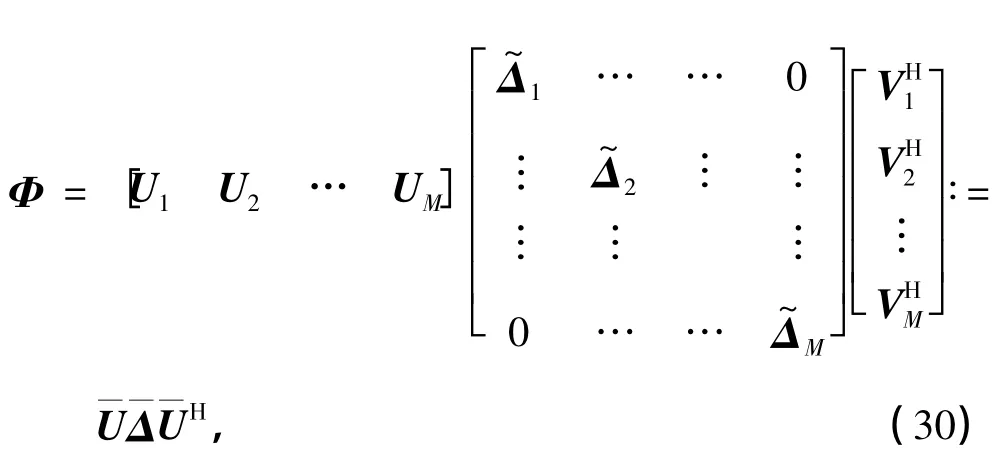
将式(30)代入式(16)中,得到
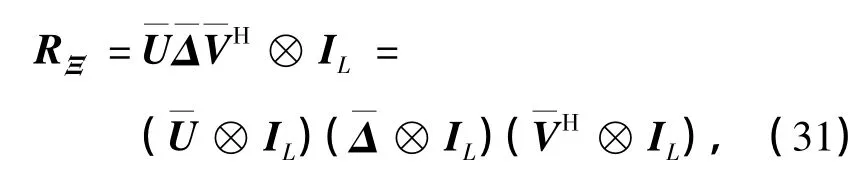
3 紧凑型G-CIR矩阵的压缩表示及信道估计
3.1 紧凑型G-CIR矩阵的压缩表示
下面利用RΞ的对角化表示推导紧凑型G-CIR矩阵的压缩表示.为了减少中未知元素的个数以简化RΞ的对角化表示,将对角线上较小的元素作为建模误差舍去,仅保留前T(T≪N)大的元素,并写成对角阵,那么式(30)可以近似写成
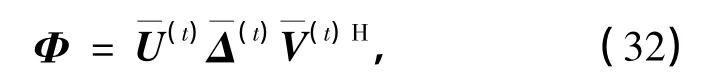
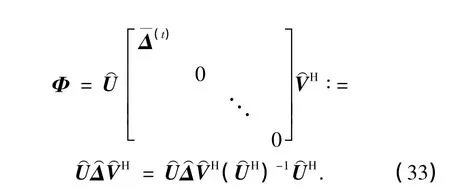
将式(32)代入式(16),得到
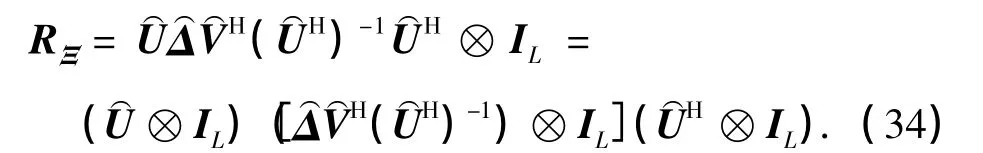
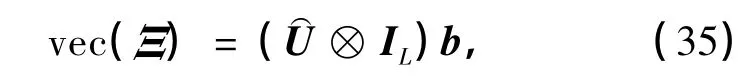
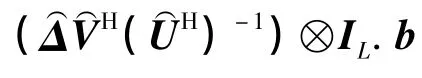
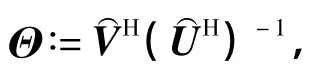
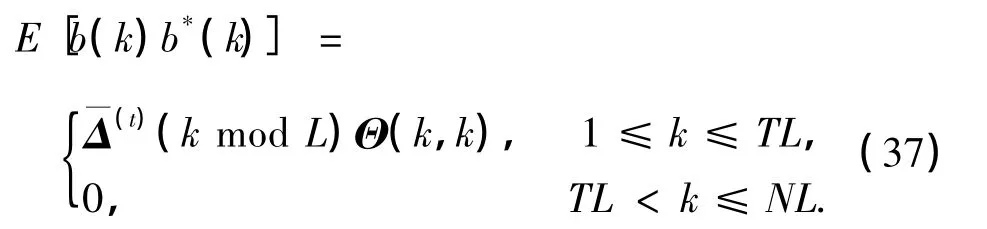
由b(k)的均方可知,列向量b中仅前TL个元素非0,这些非0元素对应的是⊗IL的前TL个列向量,即⊗IL,而其余的列向量均与b中的0元素相乘,所以可以省去.由此,式(35)可以重写为
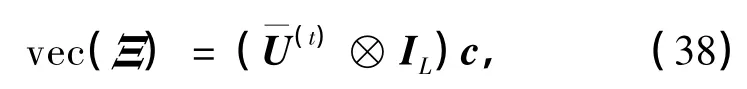
式中,TL维的列向量c由b的前TL(TL≪N)个元素组成,即c=[b(1),b(2),…,b(TL)]T.由此,就得到了紧凑型G-CIR矩阵的一种压缩表示.
3.2 等效信道模型及信道估计
为了利用3.1节得到的紧凑型G-CIR矩阵压缩表示,必须重写式(11)中的非理想同步下的快衰落信道模型.由于卷积运算满足交换律,所以可以将式(11)中的x写成卷积形式,得到
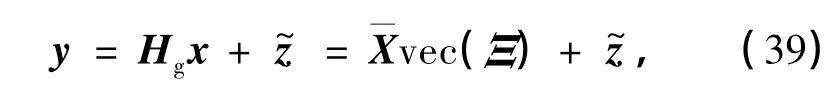
式中,
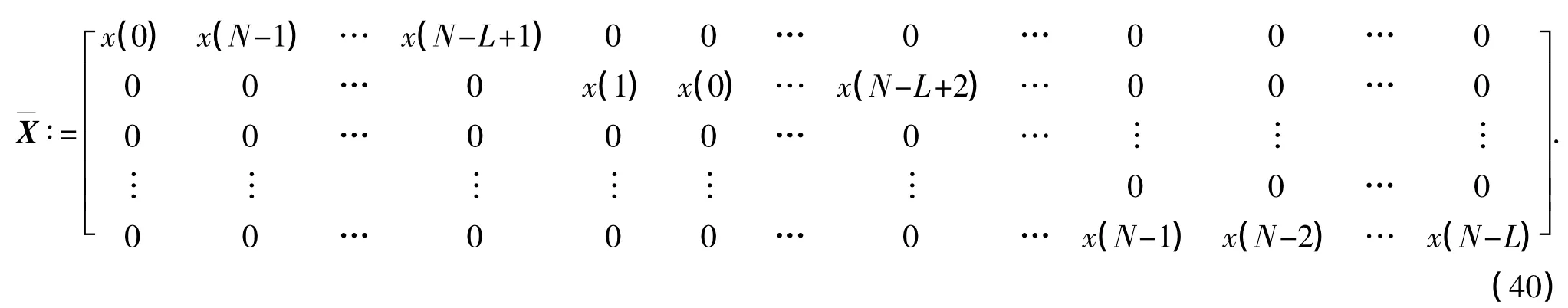
将式(38)代入式(39),得到
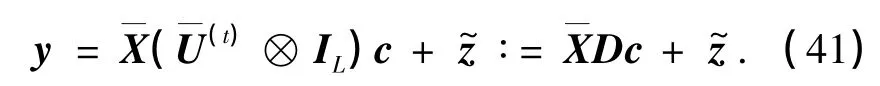
式(41)是基于紧凑型G-CIR矩阵压缩表示的等效信道模型,其中TL维的列向量c是与信道相关的待估计参数.导频方程个数只需大于TL个便可以建立超定方程组,以求解列向量c.式(41)中,接收信号y中的第p个元素y(p)对应于发射信号的第p行,其中非0元素为x((p)N),x((p-1)N),…,x((p-L+1)N),(n)N表示对n作模N运算.因此,为了建立导频方程,必须采用集中式(localized)的导频模式,如果y(p)是导频信号,那么中的第p行非0元素也为导频.这样,导频方程可以表示为
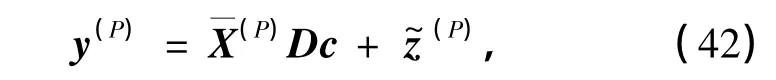
式中,(·)(P)表示导频处的信号.与传统信道估计建模方法不同,式(42)的导频方程组中仅含有导频数据,非导频数据只位于非导频方程中,因此,并不会对信道估计产生影响,从而减小了建模误差.利用最小二乘(LS)估计器求解式(42),得到c的估计值为
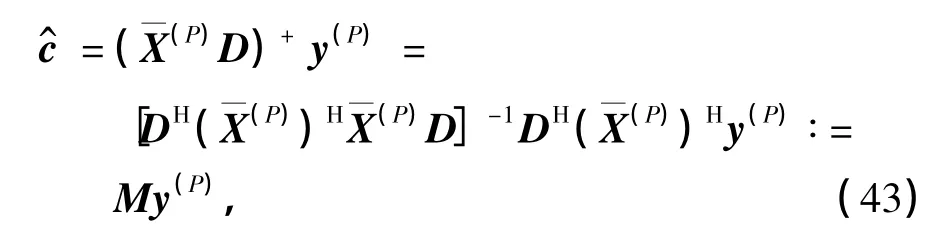
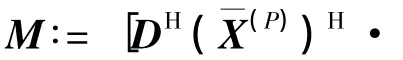
为了从c中重构出G-CIR矩阵,必须建立二者之间的关系式.根据Kronecker积的性质[17],可以将式(41)写成
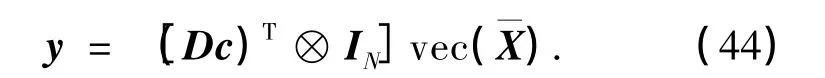
由于矩阵X—与向量x中的非0元素是相同的,那么根据向量化算子vec(·)的性质[17],可以用交换矩阵将x中的元素重新排列到vec(X—)中,即
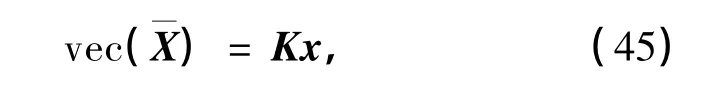
式中,K为交换矩阵,其每一行最多仅有一个非0元素,且该非0元素为1.将式(45)代入式(44)中,得到
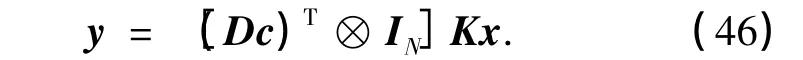
结合式(11)和(46),可得c与G-CIR矩阵的闭式表达式为
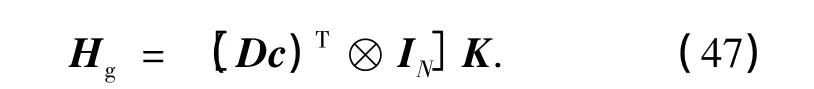
根据式(43)和(47),可以通过c^重构出G-CIR矩阵,即
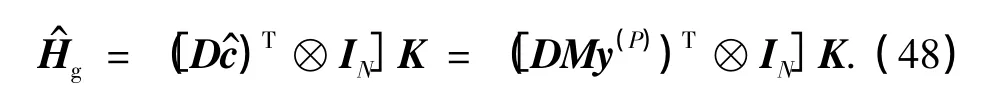
4 仿真分析
设OFDM系统采用四相差分相移键控(quadriphase differential phase shift keying,QDPSK)调制,载波频率为3.5 GHz,采样率为0.75 MHz,子载波个数N=1 024,OFDM符号周期为1 365.3 μs,保护间隔为13.3 μs,最大可辨多径数L=4.信道冲击响应符合Jakes模型,仿真中分别考虑最大多普勒频偏为1.0和1.5 kHz 2种情况.
图2给出了本研究提出的算法在非理想载波同步下的快衰落信道估计中的BER性能,其中分别考虑了最大多普勒频偏为1.0和1.5 kHz 2种情况,而CFO方面则比较了归一化频偏为0.2和0.5时的2种情况.仿真中,fd=1.0和1.5 kHz 2种情况下所对应的导频比例分别为5.00%和6.25%,而对应的T分别取6和8.仿真结果表明,在信噪比SNR为20 dB时,系统的BER性能接近10-3.
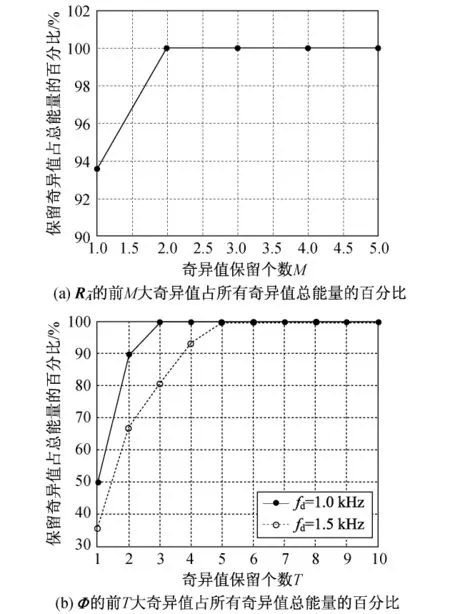
图1 与Φ中保留奇异值占所有奇异值总能量的百分比Fig.1 Percentage energy of the reserved singular values inand Φ
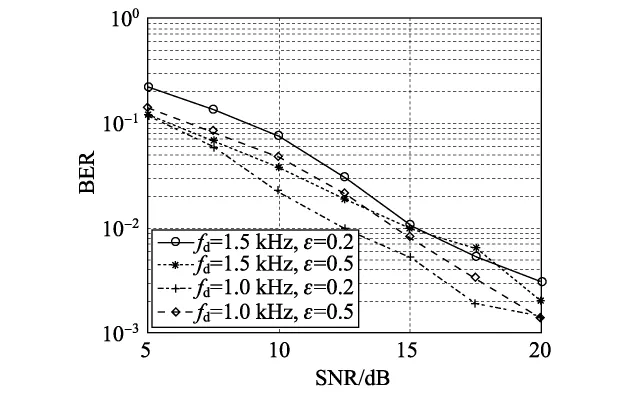
图2 非理想载波同步下的系统BER性能Fig.2 BER performance of the system with imperfect carrier synchronization
5 结束语
本研究针对非理想载波同步下的OFDM系统中无法同时克服CFO和快衰落信道的问题,提出了一种非理想载波同步下的OFDM快衰落信道估计算法,建立了非理想载波同步快衰落信道模型,其中G-CIR矩阵的提出将频偏归入信道矩阵中.虽然其自相关矩阵是随机的,但本研究提出的G-CIR矩阵的对角化方法避免了该随机性对信道估计的影响.由G-CIR矩阵的对角化表示推导出了基于信道核向量的紧凑型CIR矩阵压缩表示,该表示方法将GCIR矩阵中的未知元素个数减少到TL(TL≪N)个,从而能够得到超定的导频方程组,而较少的待估计参数也降低了导频比例,并且其离线计算的特点降低了在线计算的复杂度.仿真结果表明,本研究提出的算法在非理想载波同步下可以对快衰落信道进行有效估计,并使系统获得良好的BER性能.
[1] 和欣,张晓林.非理想载波同步对多载波直扩系统的性能影响[J].电波科学学报,2011,26(2):323-331.
[2] WANGC L,HUANGY C.Intercarrier interference cancellation using generalphase rotated conjugate transmission for OFDM systems[J].IEEE Transactions on Communications,2010,58(3):812-819.
[3] KIMJ G,LIMJ T.MAP-based channel estimation for MIMO-OFDM over fast Rayleigh fading channels[J].IEEE Transactions on Vehicular Technology,2008,57 (3):1963-1968.
[4] ZHAOY,HAGGMANS G.Intercarrier interference selfcancellation scheme for OFDM mobile communication systems[J].IEEE Transactions on Communications,2001,49(7):1185-1191.
[5] ARMSTRONGJ.Analysis of new and existing methods of reducing intercarrier interference due to carrier frequency offset in OFDM [J]. IEEE Transactions on Communications,1999,47(3):365-369.
[6] CHENY Y,ZHENGZ W,WANGX Y.Research on the intercarrier interference self-cancellation algorithms for the OFDM systems[C]∥2011 International Conference on Internet Technology and Applications(iTAP).2011:1-4.
[7] LIZ,XIAX G.An Alamouti coded OFDM transmission for cooperative systems robust to both timing errors and frequency offsets[J].IEEE Transactions on Wireless Communications,2008,7(5):1839-1844.
[8] ZHOU K, XIAO L Y. Research ofintercarrier interference cancellation for highly mobile OFDM system[C]∥2011 International Conference on Electrical and Control Engineering(ICECE).2011:4658-4661.
[9] RABBIM F,HOUS W,KOC C.High mobility orthogonal frequency division multiple access channel estimation using basis expansion model[J].IET Communications,2010,4(3):353-367.
[10] CHIT,CHENX B,WANGL D,et al.Inter-channel interference correlation matrix in OFDM system based on GCE-BEM [C]∥ 2010 The 12th International Conferenceon Advanced Communication Technology (ICACT).2010:19-22.
[11] LEUSG.On the estimation of rapidly time-varying channels[C]∥ European Signal Processing Conference (EUSIPCO).2004:2227-2230.
[12] TOMASINS,GOROKHOVA,YANGH,et al.Iterative interference cancellation and channelestimation for mobile OFDM [J].IEEE Transactions on Wireless Communications,2005,4(1):238-245.
[13] DUZ,SONGX G,CHENGJ,et al.Maximum likelihood based channelestimation formacrocellular OFDM uplinks in dispersive time-varying channels[J].IEEE Transactions on Wireless Communications,2011,10 (1):176-187.
[14] HUNGN L,THOL N,TRANN H.Iterative receiver design with joint doubly selective channel and CFO estimation for coded MIMO-OFDM transmissions[J].IEEE Transactions on Vehicular Technology,2011,60 (8):4052-4057.
[15] QUF Z,YANGL Q.On the estimation of doublyselective fading channels[J].IEEE Transactions on Wireless Communications,2010,9(4):1261-1265.
[16] HUNGN L,THOL N.Pilot-aided joint CFO and doubly-selective channel estimation for OFDM transmissions[J].IEEE Transactions on Broadcasting,2010,56(4):514-522.
[17] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004:101-113.
