基于热轧生产实绩的变形抗力模型参数确立

王 健，肖 宏，郭振华

（1.燕山大学国家冷轧板带装备及工艺工程技术研究中心，河北秦皇岛，066004；2.燕山大学机械工程学院，河北秦皇岛，066004；3.江苏徐州工程机械研究院，江苏徐州，221004）

影响轧制力最主要的因子是金属塑性变形抗力［1－3］，金属变形抗力不仅与材料变形温度、变形速度和变形程度有关，而且还受材料化学成分及组织状态影响［4］。目前变形抗力建模主要有两种方法，一种是解析法［5－7］，另一种是ANN神经网络法［8－9］，无论哪种方法都不可能对模型进行准确无误的预测［5］。研究表明，根据现场数据得出未知材料变形抗力模型，对于在线轧制控制更具实际意义。戴铁军等［10］应用Gleeble－1500试验机研究30MnSi钢变形抗力；陈连生等［11］应用Gleeble－1500研究低碳含铌双相钢变形抗力；孙蓟泉等［12］应用Gleeble3500热／力模拟实验机研究SPHC钢的热变形行为。上述变形抗力模型的建立均用到了周纪华、管克智公式［3］。

本文基于带钢热连轧实测数据，选用文献［3］变形抗力数学模型，用单纯形法对热轧带钢16个钢种的变形抗力系数进行优化回归，将回归所得变形抗力系数模型用于不包含测试样本的轧制力预报，旨在提高板带轧制过程预设定和控制模型的精度。

1 轧制力和变形抗力理论模型

采用基于OROWAN变形区力平衡理论的SIMS公式计算热轧带钢轧制力，其理论模型［13］为式中：P为轧制力，k N；B为带钢宽度，mm；lc为考虑压扁后的轧辊与轧件接触的水平投影长度，mm；Qp为考虑接触弧上摩擦力造成应力状态的影响系数；Km决定于金属材料化学成分以及变形的物理条件，一般取Km＝1.15σ（σ为变形抗力，MPa）。

基于钢的化学成分、组织状态及热力学条件对变形抗力影响的分析，采用文献［3］变形抗力模型，其基本形式为

式中：T为变形温度，K；σ0为基准变形抗力，MPa；u为应变速率，s－1；ε为变形程度（真应变）；a1～a6为取决于材料化学成分的回归参数。

2 基于实测数据的变形抗力模型

2.1 建模思路

变形抗力模型的构建实质是对式（2）中参数的确定。利用热连轧机上的检测装置，通过实测方法，测得不同温度、变形量及变形速率下的轧制力，再通过式（1）反求出所对应的变形抗力；由实测得到的大量轧制力和变形抗力数据所构建的变形抗力模型参数需要进行优选，本文采用单纯形优化法，对7种碳素钢、9种合金钢的变形抗力模型参数进行回归优选。

2.2 模型回归参数

从实测数据中提取普通碳素钢、合金钢等16种钢的轧制力及相应变形参数共280组数据，将实测数据代入式（1）、式（2），求得变形抗力公式中σ0和a1～a6的值，再将求得的σ0和a1～a0的值代入变形抗力和轧制力公式中，得到轧制力的计算值，以实测值与预测值之间的均方根误差作为评价函数［14］，其表达式为

式中：yi为实测值；f（xi）为预测值；n为样本数目。

RMSE值越小，预测值和实测值越接近，说明所建模型预测性能越好，精度越高。根据单纯形法［15］基本原理，需给出回归系数的初始值。确定σ0和a1～a6的最大值、最小值和初始值，分别取不同初始值σ0，得出各钢种的变形阻力回归参数。对于碳素钢［3］，σ0和a1～a6的最大值分别为200、－2、5、1、0、1、3，σ0和a1～a6的最小值分别为100、－4、2、0、－1、0、1，a1～a6的初始值选取为－3、3.5、0.5、－0.5、0.5、2，σ0的初始值分别为110、120、130、140、150、160、170、180、190；对于合金钢［3］，σ0和a1～a6的最大值分别为300、－1、5、1、0.5、1、3，σ0和a1～a6的最小值分别为100、－5、2、0、－1、0、1，a1～a6的初始值为－3、3.5、0.5、－0.25、0.5、2，σ0的初始值分别为110、120、130、140、150、160、170、180、190、200、210、220。采用相对误差加权算术平均值法，对以上各初始值的相对误差进行统计分析，其中最优值即为该钢种的优化回归参数。

相对误差加权算术平均值为

式中：xi为各相对误差区间样本个数；wi为各相对误差区间所对应的权重数；m为样本总数。

设相对误差在0～1%时的权重为1%，1%～2%时的权重为2%，2%～3%时的权重为3%，以此类推，由式（4）计算各初始值所对应的相对误差加权算术平均值。

回归后的各钢种变形抗力模型参数如表1所示。在碳素钢及合金钢中分别以SPHC钢和BN1P钢为例，其基准变形抗力误差加权平均值如图1、图2所示。SPHC、BN1P钢轧制力计算值与实测值比较如图3所示。碳素钢及合金钢轧制力的计算值与实测值误差分析如表2、表3所示。

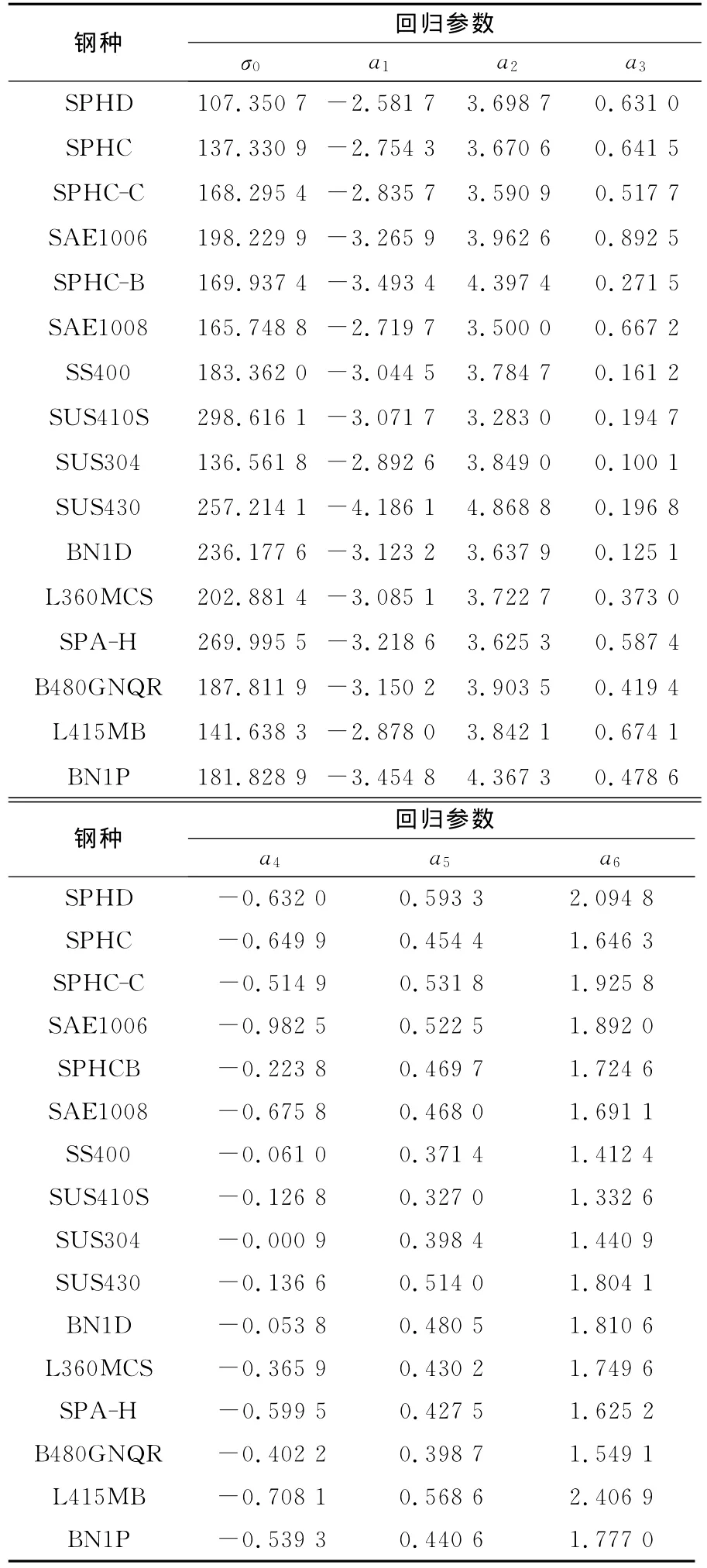
表1 回归后的各钢种变形抗力模型参数Table 1 Parameters of deformation resistance model for steels after regression

从表1中可以看出，回归后的各钢种变形抗力模型参数的取值均落在初值范围内。图1、图2表明，对应每一基准变形抗力初始值，均会出现一个最低点的误差加权算术平均值，即可选为基准变形抗力的回归初始值。从图3中可以看出，回归样本数据中碳素钢SPHC与合金钢BN1P的轧制力计算值与实测值拟合很好，其拟合直线斜率大于0.99。由表2、表3可以看出，回归后的变形抗力模型轧制力计算值与实测值相关系数均大于0.99，其拟合直线斜率接近1，说明回归后的变形抗力模型预报精度较高。

图1 SPHC钢基准变形抗力误差加权平均值Fig.1 Error weight arithmetic for SPHC

图2 BN1P钢基准变形抗力误差加权平均值Fig.2 Error weight arithmetic for BN1P

图3 SPHC、BN1P钢轧制力计算值与实测值比较Fig.3 Comparision between calculated average values and measured rolling force for SPHC and BN1P steels

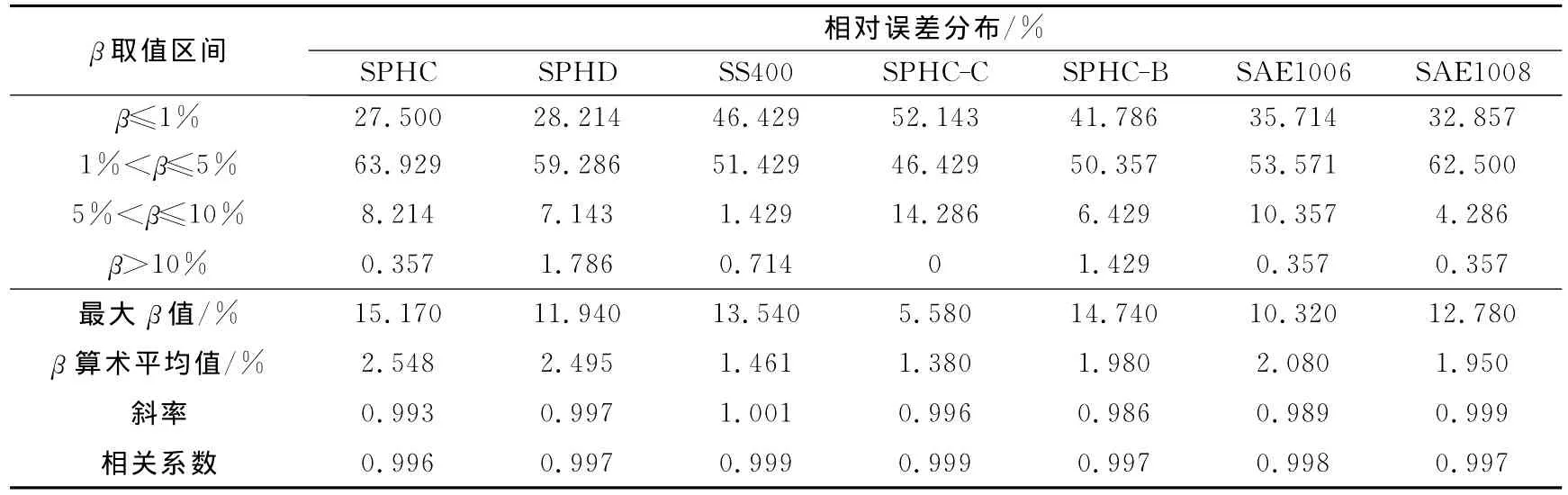
表2 碳素钢轧制力计算值与实测值误差分析Table 2 Error analysis of calculated and measured rolling force for carbon steel

表3 合金钢轧制力计算值与实测值误差分析Table 3 Error analysis of calculated and measured rolling force for alloy steel

2.3 深度变形抗力模型验证

为了深度验证回归变形抗力模型的精度及拟合性，在相同轧线上测取不同时段、不同规格、不同钢种的轧制力数据，利用回归所得变形抗力模型进行轧制力计算，对其计算值与实测值进行误差验证，碳素钢、合金钢轧制力计算值与实测值误差验证分别如表4、表5所示。SPHC、BN1P钢轧制力相对误差分布如图4所示。SPHC、BN1P钢轧制力计算值与实测值比较如图5所示。

表4 碳素钢轧制力计算值与实测值误差验证Table 4 Error verification analysis of calculated and measured rolling force for carbon steel

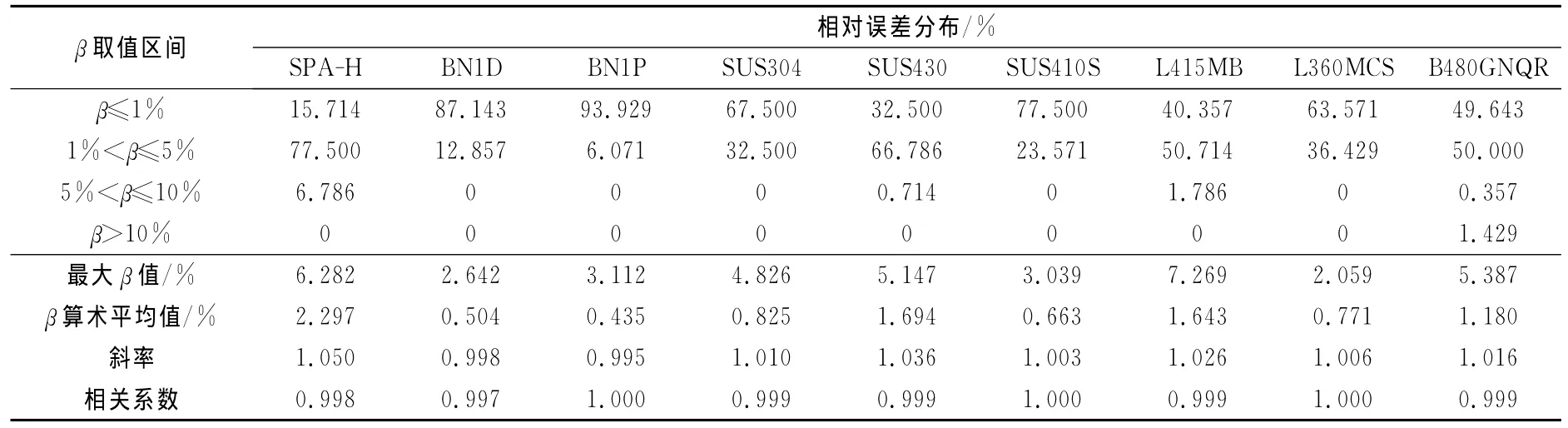
表5 合金钢轧制力计算值与实测值误差验证Table 5 Error verification analysis of calculated and measured rolling force for alloy steel

图4 SPHC、BN1P钢轧制力相对误差分布Fig.4 Range of error for SPHC and BN1P steel

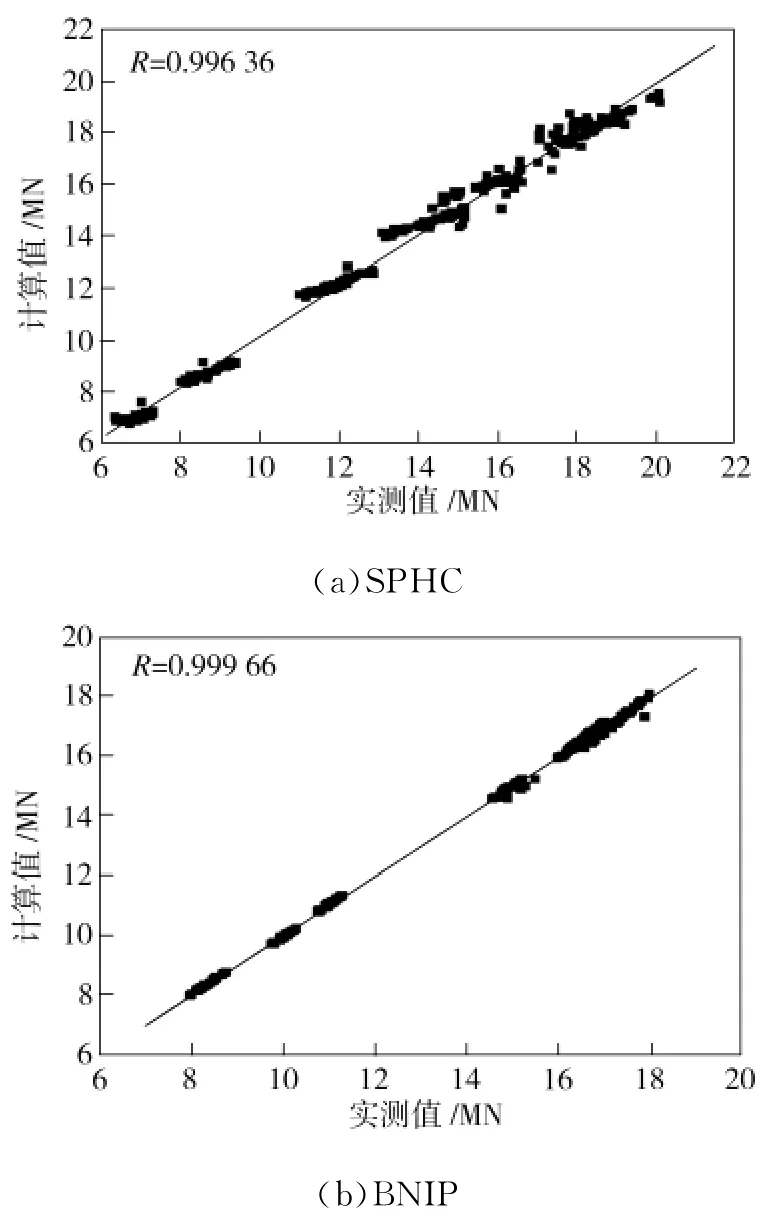
图5 SPHC、BN1P钢轧制力计算值与实测值比较Fig.5 Comparision between calculated and measured rolling force for SPHC and BN1P steels

由表4、表5及图4、图5可以看出，SPHC钢轧制力计算值与实测值相对误差算术平均值为2.162%，最大误差值为10.52%；BN1P钢轧制力计算值与实测值相对误差算术平均值为0.435%，最大相对误差值为3.112%，不超过5%；所得拟合直线斜率均接近1，SPHC钢轧制力计算值与实测值间相关系数为0.996，BN1P钢轧制力计算值与实测值间相关系数为0.999。进一步说明，经参数回归后的模型拟合性好，预报精度高。

3 结论

（1）基于数据实测通过回归变形抗力模型中参数的方法，所构建的变形抗力模型能综合体现诸因素对变形抗力的影响。

（2）将优化回归所得的变形抗力模型用于不包含测试样本的轧制力预报，不仅能够重现样本数据的轧制力，还能精确预报非样本数据。

［1］ 陈爱玲.变形抗力预测模型及其应用研究［J］.计算机集成制造系统，2007，13（9）：1 816－1 819.

［2］ 陈程，尹海青，曲选辉，等.钼塑性变形阻力数学模型的研究［J］.塑性工程学报，2007，14（2）：7－10.

［3］ 周纪华，管克智.金属塑性变形阻力［M］.北京：机械工业出版社.1989：209－215.

［4］ 贺毓辛.轧制工程学［M］.北京：化学工业出版社，2009：49－50.

［5］ 李英，刘建雄，柯晓涛.轧制变形抗力数学模型的发展与研究动态［J］.钢铁研究，2009，37（6）：59－62.

［6］ 管克智，周纪华，朱其圣，等.热轧金属塑性变形阻力研究［J］.北京钢铁学院学报，1983（2）：123－138.

［7］ Lin Yongcheng，Chen Mingsong，Zhang Jun.Modeling of flow stress of 42Cr Mo steel under hot compression［J］.Materials Science and Engineering A，2009，499（1－2）：88－92.

［8］ K P Rao，Y K D V Prasad.Neural network approach to flow stress evaluation in hot deformation［J］.Journal of Materials Processing Technology，1995，53（3－4）：552－566.

［9］ Shashi Kumar，Sanjeev Kumar，Prakash.Prediction of flow stress for carbon steels using recurrent self－organizing neuro fuzzy networks［J］.Expert Systems with Applications，2007，32（3）：777－788.

［10］戴铁军，刘战英，刘相华，等.30MnSi钢金属塑性变形抗力的数学模型［J］.塑性工程学报，2001，8（3）：17－20.

［11］陈连生，狄国标，张洪波，等.低碳含铌钛双相钢的塑性变形抗力模型［J］.塑性工程学报，2007，14（6）：127－129.

［12］孙蓟泉，张金旺，王永春.SPHC钢热变形行为的研究［J］.钢铁，2008，43（9）：44－48.

［13］刘文仲，吕志民.热连轧带钢压力数学模型及其建模方法研究［J］.钢铁，2002，37（5）：34－37.

［14］霍倩，李书全，王文元，等.遗传算法应用于多元非线性回归模型求参的研究［J］.河北农业大学学报，2002，25（2）：107－108.

［15］刘惟信.机械最优化设计（第二版）［M］.北京：清华大学出版社，1994：110－115.