基于双线性内插的图像处理算法及其优化

曹亚君，邵玉兰

(商丘职业技术学院计算机系，河南商丘476000)

数字图像处理是指用计算机对图像经过采样和数字化后的二维数组进行分析处理，以达到所需结果的技术，图像处理所涉及的应用领域也包括了人们工作、学习和生活中的各个方面。在图像处理技术中最常见的就是图像放大，也就是将一幅低分辨率的图像获得它的高分辨率版本的一种图像处理技术。在航天航空、生物医学工程、通信工程以及工业生产等各方面有着非常广泛的应用。

1．数字图像处理中的插值算法

插值算法是一种应用十分广泛的方法。在数学表示法中，通常用y=f(x)表示一条平面曲线(若是二维函数则为曲面)，为了代替原来的函数y=f(x)中的数据，就需要找到另一个函数φ=f(x)，找寻这个替代的函数即为插值。图像插值就是利用已知邻近像素点的灰度值来产生未知像素点的灰度值，以便由原始图像再生出具有更高分辨率的图像。［1］插值算法会自动选择信息较好的像素作为增加的像素，而并非只使用临近的像素，所以在放大图像时，图像看上去会比较平滑、干净。插值是数字图像处理领域里一个很大的分支，对于增加的未知像素采用哪一种插值方式是图像放大算法的关键。常用的插值算法有最邻近插值算法(Nearest Neighbor interpolation)、双线性内插算法(Bilinear interpolation)和双立方插值算法(Bicubic interpolation)。

最邻近插值算法是最简单的一种插值算法，当图片放大时，缺少的像素通过直接使用与之最接近的原有的像素的颜色生成，也就是把原始像素直接复至到其领域内。它是三种内插值方式中质量最差的一种，放大后的图像会出现明显的锯齿或方块，效果比较模糊，比较适合于放大倍数较小且对质量要求不高的场合。［2］

双线性内插算法是沿X轴方向和Y轴方向分别对未知像素点进行一次线性插值取样，然后求得加权平均值，即为该点像素的颜色值。这种算法极大地消除了锯齿现象，放大后的图像平滑性好，但会使图像边缘模糊，在计算速度与质量两个方面都居于三种方法中间地位。双立方插值算法是在沿X轴、Y轴和对角线Z轴方向对未知像素点取样，求得该点邻近的16个像素点值，依据对其远近影响进行插值计算，得到该点像素的颜色平均值。虽然双立方插值算法可以得到最佳画质，但是它的计算复杂度实在太大了，即使采用了整数优化和查表法，也将耗去大量的CPU资源，不太实用。本文主要讨论在数字图像的实时处理中，用途最广的双线性内插算法及其优化。

2．双线性内插图像放大算法及优化

2．1．双线性内插算法原理

双线性内插，又称双线性插值法。用数学表示法来表示，双线性内插是插值函数的一种具有两个变量的线性插值扩展，其主要原理是对未知像素点邻近的四个像素点在X轴和Y轴方向进行线性插值。双线性插值和最近邻点插值法相比，可以产生一个能保持连续性和连通性的光滑映射，产生更令人满意的效果。［3］将高为strH、srcW的图像插值为高和宽分别为desH、desW的插值图像，插值前后图像的坐标分别用(x，y)和(i，j)来表示。则此图像插值后图像中任一点的像素值可由插值前图像中坐标为(x，y)，(x+1，y)，(x，y+1)和(x+1，y+1)所对应的4个像素的值确定。［4］如图1所示，即

式中:u，t分别为插值点坐标(i，j)与坐标(x，y)在x和y方向的浮点距离，且0≤t＜1，0≤u＜1，由下列计算得到

对上述计算过程类推，可计算得插值图像中其他各点的像素值。

图1 目标图像像素灰度值的确定

2．2．基于边缘的内插值优化算法

双线性内插算法使放大后的图像平滑性好，较好地消除了锯齿现象，但其具有低通滤波性质，该方法会使高频分量受损，图像轮廓有一定模糊。因此为了减少双线性内插算法使图像边缘模糊的问题，对其算法优化，主要是进行锐化处理，使图像视觉效果更好，图像轮廓得到加强。

首先使用双线性内插值对原始图像进行放大，然后将放大后的图像使用高通滤波让高频分量通过，使图像的边缘或线条等细节变得清晰，实现图像锐化。为了达到图像实时处理的需要，因此使用线性的FIR滤波器对图像边缘处理。［5］

其中w(x，y)为高通滤波算子的系数，p(x，y)为中心点的像素值。

在YUV数据格式中，以图像前两行像素处理的数据为例，原始图像第一行和第二行的128个Y分量数据如下表1所示。

表1 原图像Y分量数据

对原始图像使用双线性内插算法放大2倍后，由每行的128个数据插值可得到两行256个Y分量数据，如下表2所示。放大后的UV数据分量也通过此插值计算得到。

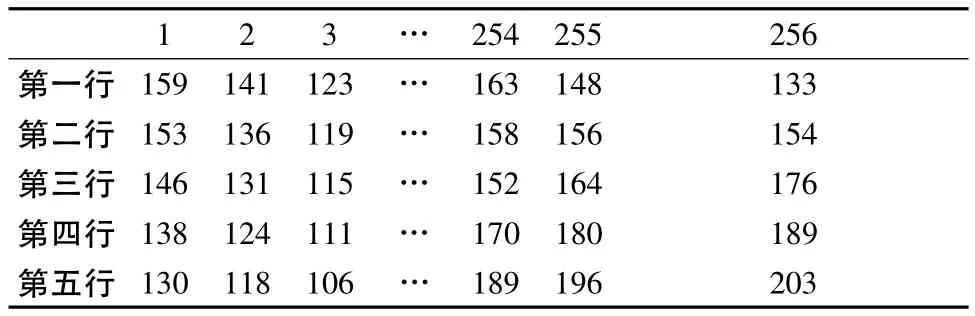
表2 放大后图像Y分量数据

在对原始图像插值放大后，接着用线性的FIR高通滤波器锐化。由于这种FIR滤波器必须满足滤波器的中心系数为正数，其他系数为负数，故这里使用线性高通滤波器3×3模板的典型系数，如式(2)所示。将放大后图像的Y分量数据进行两次缓存处理，就得到了一个的窗口，每个像素点的系数如式(2)所示。

3．实验结果与分析

首先将原始256×256的灰度Lena图像降采样到128×128图像，结着再分别应用双线性内插算法及其优化算法对图像再进行放大处理，对比分析还原之后的效果。如图2所示，其中(a)为降采样后的128×128图像，(b)为应用双线性内插算法的结果，图像较平滑，但边缘轮廓有一定模糊，(c)为应用边缘增强处理优化算法的结果，与图(b)相比，图像的边缘轮廓较清晰，如眼部、帽沿等边缘部分，使处理后的图像效果更好。

图2 插值算法效果对比图

4．结束语

在数字图像的实时处理中，放大图像是一种常用技术。考虑到运算速度、硬件等条件，采用双线性内插是最实用的一种算法。因放大后的目标像素值是其4个邻近像素的加权平均值，具有低通滤波的性质，高频分量受损，所产生的图像边缘会有一定的模糊，故本文对双线性内插放大图像算法进行优化处理。加强了图像边缘的锐化，采用高通滤波器使图像的高频分量信息得以通过，提高了边缘细节的清晰度。因此，优化的双线性内插算法在图像的实时放大中具有更好的效果。

［1］符祥，郭宝龙．图像插值技术综述［J］．计算机工程与设计，2009，30(1):141 －144．

［2］刘丽君，骆婷．插值法在图像处理中的应用［J］．硅谷，2009(9):9－10．

［3］陈宝平，赵俊岗，尹志凌．双线性插值算法的一种快速实现方式［J］．北京电子科技学院学报，2004，12(4):21 －23．

［4］［美］冈萨雷斯．数字图像处理［M］．阮秋奇，阮宇智，译．北京:电子工业出版社，2005:9．

［5］戴玉良．用DSP实现FIR数字滤波器［J］．台州学院学报，2006，28(6):43 －46．