对一道高考试题的讨论
2012-01-23杨宋鹏姚新利
杨宋鹏 姚新利
(铜川市耀州中学 陕西 铜川 727100)
文献[1]刊登了对2010年普通高等学校招生全国统一考试(上海卷)物理试题的评析,其中第24小题,给出了两种解法,这两种解法的确简单,但是读完之后,总觉得这样的解法没有考虑初始位置间的夹角,有些不妥.课堂上给学生讲完上述两种解法后,大部分学生同样不能理解:为什么不考虑初始位置间的夹角?从图1所示位置开始到第一次共线,a,b运动过的圆心角的差值并不等于π.思考再三,原来教师总是向学生强调重视过程的分析,但学生对题目中a,b物体运动过程中的关系并没有弄清,上述两种解法中同样没有过程的分析.为什么不考虑初始位置间的夹角,的确存在思维上的漏洞.于是笔者在课堂上引导学生分析,找到了两种更好的、更常规的解法,现在与大家分享.
题目:如图1所示,3个质点a,b,c质量分别为m1,m2,M(M≫m1,M≫m2).在质点c的万有引力作用下,a,b在同一平面内绕c沿逆时针方向做匀速圆周运动,轨道半径之比为ra∶rb=1∶4,则它们的周期之比Ta∶Tb=______;从图示位置开始,在b运动一周的过程中,a,b,c共线了______次.
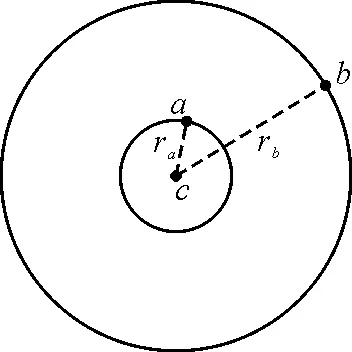
图1
解析:万有引力提供向心力,则
所以Ta∶Tb=1∶8.第一问的求解与参考答案相同.
现将第二问的两种常规解法介绍如下.
解法一:物理过程分析法
第一问已经求得Ta∶Tb=1∶8,即b物体运动1周的时间内a物体运动8周.据此,将b物体运动的轨迹圆周分成8等份,如图2所示.
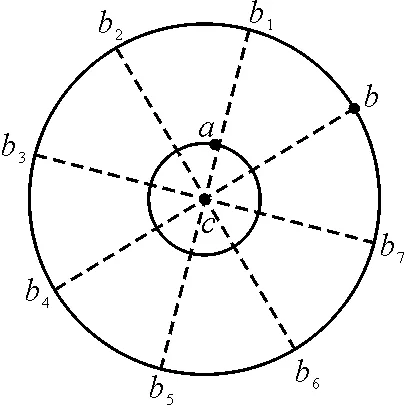
图2
在a物体运动第1周的时间内,b物体从图2中的b位置到b1位置,此过程中,a的线速度大,质点a,b,c第一次共线出现在当a在b4cb5区域运动的过程中(a、b在c的两侧);由于a最后回到出发点,因此a,b,c第二次共线出现在当a在bcb1区域运动的过程中(a,b在c的同侧).所以在a运动第1周的时间内,质点a,b,c共线出现2次.
在a运动第2周的时间内,b从图2中的b1位置到b2位置,a的线速度大,b的线速度小,a,b,c的第一次共线出现在当a在b5cb6区域运动的过程中(a、b在c的两侧),此后a最后回到出发点,不可能再出现a,b,c共线的情形.所以在a运动第2周的时间内,a,b,c共线出现1次.
在a运动第3周的时间内,b从图2中的b2位置到b3位置,a的线速度大,b的线速度小,质点a,b,c的第一次共线出现在当a在b2cb3区域运动的过程中(a、b在c的同侧),相当于a超过b时;质点a,b,c第二次共线出现在当a在b6cb7区域运动的过程中(a,b在c的两侧).所以在a运动第3周的时间内,质点a,b,c共线出现2次.
同理,b从图2中的b3位置到b4位置,从b4到b5,从b6到b7,b从图中的b7位置回b位置,这几个过程中,质点a,b,c共线出现2次.而b从图中的b5位置到b6位置的过程,与b从图中的b1位置到b2位置的过程相似,质点a,b,c共线出现1次.
所以在b运动1周的时间内,质点a,b,c共线了14次.从分析求解过程可以看出:当b在a的起始位置所在的区域及其对称区域运动时,质点a,b,c共线出现1次,其他区域质点a,b,c共线出现2次,与初始位置间夹角∠acb的大小无关.
这个解法符合学生的思维习惯,便于解答学生心中的疑惑,有利于学生思维能力和分析力、动手能力的培养,但是过程繁琐,考试中较费时间.
解法二:计算法
也是利用两次共线的时间间隔t计算,但将开始计时到第一次共线的时间单列计算.
为便于理解,先分析起始位置共线的两类情况.在图3所示的两类情况中,设每隔时间t,质点a,b,c共线1次,则
(ωa-ωb)t=π
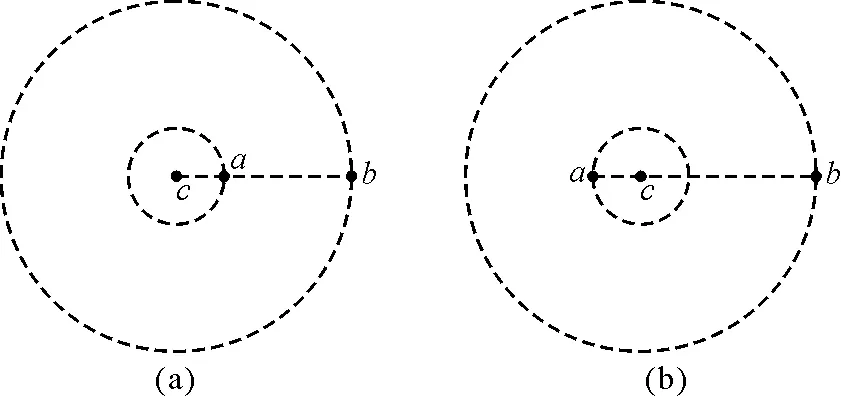
图3
所以b运动1周的过程中,质点a,b,c共线的次数为
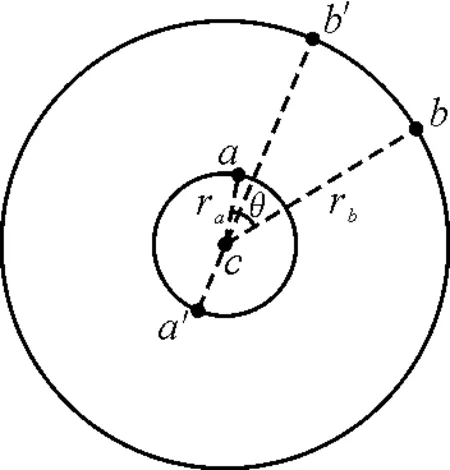
图4
本题中,第一次共线后的其他共线,均可视为上述情况.这样考虑起始夹角∠acb=θ.设由图4所示a,b位置运动到第一次共线(即a,b运动到a′,b′,位置)用时为t1,则由图4中的关系可得
ωat1+θ-ωbt1=π
此后的情形与图3所示情形相同,即设每隔时间t,质点a,b,c共线1次,则
(ωa-ωb)t=π
那么在b运动1周的时间内,质点a,b,c共线的次数为
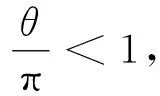
这种解法学生从过程分析、数学运算两个方面都容易理解和接受.但是,学生往往容易产生一个错误的推论:若θ>π, 那么n=15.其实这个想法是错误的.
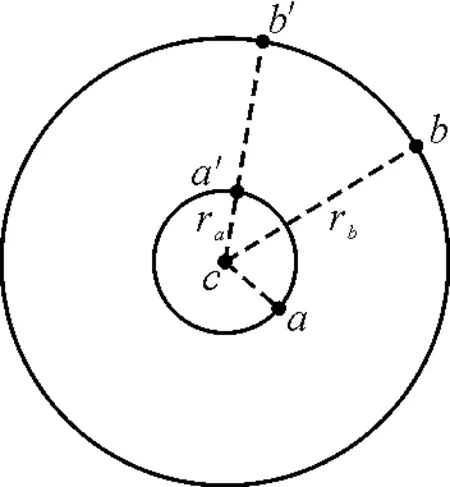
图5
分析如下:设由图5所示a,b位置运动到第一次共线(即a,b运动到a′,b′,位置)用时为t1,则由图5中的关系可得
ωat1+θ-ωbt1=2π
此后的情形与上一种情形相同,即设每隔时间t,质点a,b,c共线1次,则
(ωa-ωb)t=π
那么在b运动1周的时间内,质点a,b,c共线的次数为

这样,学生更容易理解和接受,而且也证明了,结果的确与初始位置夹角θ的大小无关.
参考文献
1 宋淑光.对2010年普通高等学校招生全国统一考试(上海卷)物理试题的评析.中学物理教学参考,2010(9):44
