由面心立方(111)面间距谈几何晶体学的几个基本概念*①
2012-01-23马天平谭伟石
马天平 谭伟石
(南京理工大学理学院应用物理系 江苏 南京 210094)
1 引言
在通常的《固体物理学》和《X射线衍射学》教材[1~3]中,都表示可以采用公式
(1)
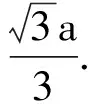
2 面心立方晶体(111)面间距的计算
出现上述问题的根本原因在于公式(1)中的指数h,k,l为密勒指数,而不是晶面指数.因此,不能将晶面指数代入此公式计算面间距.为此,需要先导出采用晶面指数计算面间距的公式.
如图1所示,选取面心立方晶体的固体物理学原胞的初基矢量为

(2)
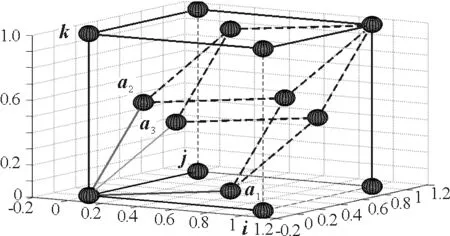
图1 面心立方晶体的原胞坐标系
式中i,j,k分别表示笛卡儿正交坐标系中三个坐标轴的单位矢量.
根据倒易点阵的定义式
计算其倒格子的初基矢量,得
(3)
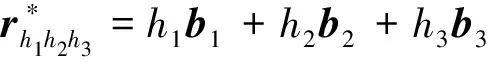
(4)

通常所使用的面间距公式(1)中面指数(hkl)是在晶胞坐标系a,b,c中确定的密勒指数.这就涉及到对晶胞和固体物理学原胞等概念的辨析.
3 几何晶体学中几个基本概念的辨析
上述问题通过基矢的适当选取得到了解决,但更本质上反映的是对几何晶体学中几个基本概念的混淆.
(1)原胞.体积最小的重复单元称为原胞或固体物理学原胞[1,2].原胞的选取不是唯一的.只要符合体积最小和周期性两个条件即可,所以原胞往往不能表达对称性.若使用威格纳-塞兹(Wigner-Seitz)原胞[2],则既能反映晶格的全部对称性,也能反映周期性.
(2)晶胞.又称单胞,或称结晶学原胞,是晶体结构的最小重度单元,即在能反映晶体对称性的前提下选取体积尽量小的重复单元.实际的晶体结构可以看成是晶胞在三维方向周期性地堆砌而成.在晶胞中,可含有一个或多个格点,体积为原胞的一倍或数倍.在晶胞中所选取的沿晶轴的三个矢量通常也称为轴矢.晶胞的概念强调了对称性.
(3)晶面指数.在固体物理学原胞的基矢坐标系中,晶面在三个基矢a1,a2,a3方向上的截距以基矢长度作为单位进行度量后取倒数,约去公因子,得到一组互质的整数,即为该晶面的晶面指数,常用(h1h2h3)表示[4].
(4)密勒指数.在晶胞的轴矢坐标系中,晶面在三个轴矢a,b,c方向上的截距以轴矢长度作为单位进行度量后取倒数,约去公因子,得到一组互质的整数,即为该晶面的密勒指数,常用(hkl)表示.
可见,晶面指数和密勒指数的确定方法相同,但是二者之间存在的差异在于所采用的基矢量不同.
在实际应用中,人们往往习惯使用密勒指数,即使用晶胞(单胞)的基矢讨论问题.尤其在正交晶系中,通常以正交基矢对应的密勒指数讨论晶面问题.但需要注意的是,密勒指数所选取的基矢能很好地体现对称性,但并不一定对应最小的周期性单元,尤其在计算面间距的过程中,如果在概念上混淆,用密勒指数代入对应于晶面指数的公式,就会产生错误.
在面心立方晶体的轴矢坐标系a,b,c中
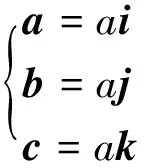
定义
计算可得
与晶面族(hkl)正交的倒格矢
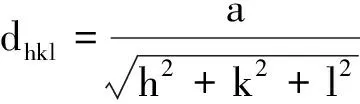
(5)
可知(hkl)为密勒指数,而不是晶面指数.
4 晶面指数与密勒指数的转换矩阵
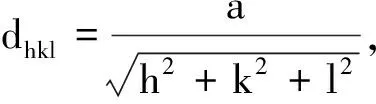
立方晶系中,设密勒指数为(hkl),晶面指数为(h1h2h3),各自对应的轴矢量与基矢量分别为
可以记为A=EC,其中
E为基矢-轴矢转换的系数矩阵.
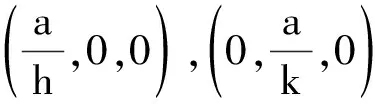
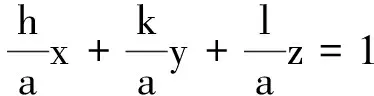
(6)
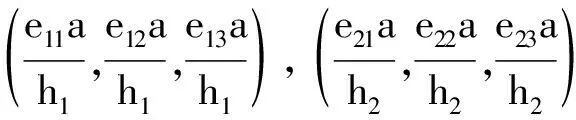
由于这三点在晶面上,故符合晶面方程(6),代入后得
写成矩阵形式为
(7)
式中的转换矩阵即基矢-轴矢转换的系数矩阵E.
由此可见,基矢-轴矢转换的系数矩阵亦为密勒指数-晶面指数的转换矩阵.同时,通过逆矩阵E-1,可以将晶面指数转换为密勒指数.
对于面心立方晶体而言,基矢-轴矢转换的系数矩阵及其逆矩阵分别为
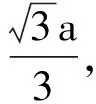
表1中列出了面心立方晶体中一些低指数晶面指数对应的密勒指数及晶面间距.将相应的晶面指数和密勒指数分别代入式(4)和式(5),计算得到的晶面间距是相同的.由表中可见,密排面(111)的晶面间距是最大的.
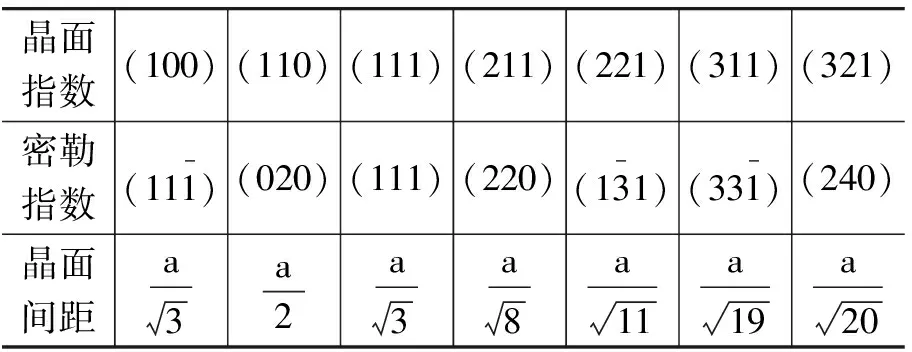
表1 面心立方晶面指数、密勒指数和面间距
5 结语
通过对面心立方晶体(111)面间距的计算,阐述了如何正确理解几何晶体学中的几个基本概念.同时,给出了晶面指数与密勒指数之间的转换矩阵,此转换矩阵可为晶体面间距的计算带来方便.
参考文献
1 黄昆原著.韩汝琦改编. 固体物理学. 北京:高等教育出版社,1988
2 韦丹. 固体物理. 北京:清华大学出版社, 2003
3 黄胜涛. 固体X射线学(一). 北京:高等教育出版社,1985
4 胡安,章维益. 固体物理学. 北京:高等教育出版社, 2007
