一道几何光学高考题的两种新解法
2012-01-23罗声苗肖炯
罗声苗 肖炯
(赣县中学 江西 赣州 341100)

图1
【题目】(2011年高考新课标全国卷第34题)一半圆柱形透明物体横截面如图1所示,底面AOB镀银(图中粗线),O表示半圆截面的圆心,一束光线在横截面内从M点入射,经过AB面反射后从N点射出.已知光线在M点的入射角为30°,∠MOA=60°,∠NOB=30°.求:
(1)光线在M点的折射角;
(2)透明物体的折射率.
方法1:原解
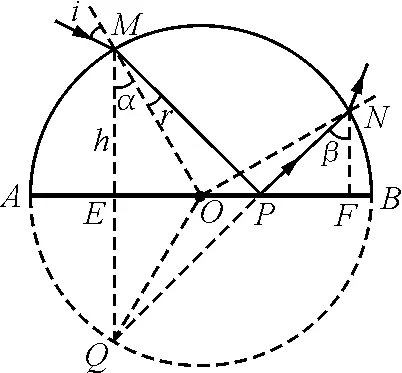
图2
如图2,透明物体内部的光路为折线MPN,Q,M点相对于底面EF对称,Q,P和N三点共线.
设在M点处,光的入射角为i,折射角为r,∠OMQ=α,∠PNF=β.根据题意有
α=30°
(1)
由几何关系得,∠PNO=∠PQO=r,∠ONF=60°,
于是
β+r=60°
(2)
根据反射定律可以知道∠MPE=∠NPF,由几何关系容易得
α+r=β
(3)
由式(1)~(3)得
r=15°
(4)
根据折射率公式有
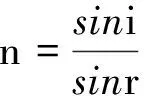
(5)
代入数据得
点评:笔者认为,原解所用到的数学知识本身并不是很难,但是作图的过程中所作的辅助线比较多,而且要把半圆的下半部分补充完整,这种情况在数学中见得比较多,在物理中应用得很少,所以,学生在考试的时候,不容易想到这种方法.
方法2:巧用几何关系EF=EO+OF=EP+PF求解
如图3,光线从M点的入射,经过AB面反射后从N点射出,透明物体内部的光路为折线MPN.过M,N点作垂线交底面AB于E,F.根据反射定律,可以知道,∠MPE=∠NPF=θ.由几何关系得
EF=EO+OF=EP+PF
(6)
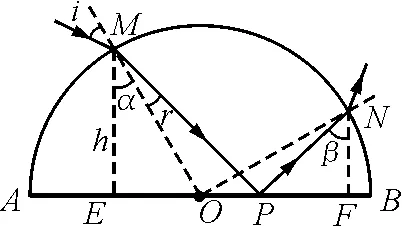
图3
其中有
EO+OF=Rcos60°+Rcos30°
(7)
(8)
由式(6)~(8)得
θ=45°
(9)
入射角为i,折射角为r, ∠MOE=60°,根据三角形外角等于相临两内角和,即
θ+r=60°
(10)
由式(9)、(10)得折射角r=15°,再根据折射率公式有

点评:这种方法充分应用EF=EO+OF=EP+PF,结合反射定律,列出等式求出θ角的大小,再应用外角与内角和的关系求出r的大小.整个过程中所作的辅助线少,用到的都是最简单的数学知识,应该说达到了用简单知识解决复杂问题的要求.
方法3:应用正弦定理求解
如图3,透明物体内部的光路为折线MPN.设在M点处,入射角为i,折射角为r,在N点射出∠ONP为r′,根据反射定律有,∠MPE=∠NPF=θ.由题意知道∠MOA=60°,∠NOB=30°.根据三角形外角等于相临两内角和得
r+θ=60°
(11)
r′+30°=θ
(12)
在△MOP中由正弦定理得
(13)
同理在△ONP中由正弦定理得
(14)
由式(13)、(14)得
r=r′
(15)
由式(11)、(12)、(15)可以求得r=15°,再根据折射率公式有
代入数据得
点评:求证r=r′的关系时,除了用到正弦定理、光的反射定律之外,并未有任何的附加条件.而正弦定理、光的反射定律都具有普遍性,所以,解题过程中得到的r=r′也具有普遍性.即在半圆形介质中,光线进入介质经底面反射再折射出来,也和圆形介质一样有这样一个普遍结论即进入介质的入射角和最后出介质的折射角大小总是相等.
