对一个准静态过程模型的讨论*

张国锋 周越

( 北京航空航天大学物理科学与核能工程学院物理系 北京 100191)( 北京林业大学理学院 北京 100083)

准静态过程是热力学中一种有重要意义的理想过程. 因为在准静态过程中，系统连续经过的每个中间态都可以近似地看成平衡态, 因此，可以用统一的宏观参量进行描述, 从而可以方便地对热力学过程中系统做功和热传递进行定量计算. 在普通物理范围内, 对热力学过程的讨论大都基于准静态过程.

在讲解准静态过程时, 不少教材都举如下模型为例[1～5]，一个气缸的活塞上放置有大量很小的砝码或者沙粒, 如果将小砝码或沙粒足够缓慢地逐个去掉, 则气缸内的气体缓慢膨胀的过程可以视为准静态过程. 为了更直观地说明准静态过程是如何取得的, 部分教材进一步做了如下论证[1～3],如果将活塞上的大砝码一次性去掉, 最开始只有活塞附近的气体开始膨胀, 减压的影响以声速在气缸中传播, 经过复杂的弛豫过程, 最终系统达到了新的平衡态，如图1(a). 在中间过程气缸内的气体处于非平衡态, 各处没有统一的压强, 因此,整个过程只有初态和末态可以在p-V图上表示出来，如图2(a); 如果把大砝码分成两个, 去掉一个后,待系统恢复平衡再去掉另一个，如图1(b), 则在p-V图上除了初态和末态外还可再标出一个中间点，如图2(b); 如果把砝码分为更多份并依次去掉，如图1(c), 则在p-V图上就可以得到一系列的中间点，如图2(c); 以此类推, 如果将砝码无限地分下去, 则在p-V图上系统从初态经过一条连续的曲线到达末态，如图2(d), 这样就构成了一个准静态过程.

图1

图2

这一论证虽然简单、直观, 但实则存在漏洞, 这可以用普通物理教材中常见的理想气体绝热自由膨胀过程来说明.

图3

考虑一个绝热的气缸, 一个隔板将气缸等分为两部分, 下部有一定物质的量的理想气体, 上部为真空. 如果将隔板撤去, 则气缸下部的理想气体会通过输运过程扩散到上部, 在气缸中形成宏观的定向运动. 最后，气体宏观运动的能量通过分子的碰撞过程转化为无规运动的能量, 气缸内的气体重新恢复平衡状态，如图3(a), 这时只有初态和末态可以标示在p-V图上，如图2(a). 如果在气缸上部中央再加上一个隔板, 去掉第一个隔板后,待气体恢复平衡再去掉第二个隔板,如图3(b), 则在p-V图上就可以增加一个中间点，如图2(b); 以此类推, 如果在气缸中添加更多的隔板, 并依次去掉，如图3(c), 在p-V图上就可以得到更多的中间点，如图2(c); 以此类推, 若令隔板数量n→∝, 根据前面提到的论证方法, 在p-V图上系统将从初态经过一条连续的曲线到达末态，如图2(d). 这样, 系统对外做功的值等于曲线下方的面积. 然而, 无论气缸中隔板的数目有多少, 理想气体始终是向真空中膨胀, 因此，对外做功应为零. 产生这个矛盾的原因在于“连点成线”的假定存在问题. 如果n个隔板在气缸上部均匀排列, 初始时刻气体的体积为V0, 去掉i个隔板后气体体积为Vi, 则有

(1)

类似地， 如果将活塞上的砝码依次去掉, 处于平衡态的中间点在p-V图上也是离散的, 那么，当n→∝时该过程是否趋向于准静态过程呢?下面定量讨论这一问题. 在图1中, 假定气缸壁和活塞都是绝热的, 截面积为S的活塞(质量忽略不计)上放置有总质量为M的n个砝码. 在初始时刻系统处于平衡状态, 活塞的高度为hn. 现将活塞上的砝码依次去掉, 每去掉一个待系统恢复平衡后再去掉另一个, 在去掉i个砝码并重新恢复平衡后, 活塞的高度、气缸内的气体压强和温度分别是hn-i,pn-i和Tn-i, 直到去掉全部砝码为止. 气缸内的气体在中间过程的一系列平衡态中满足理想气体状态方程

pn-iVn-i=pn-iShn-i=νRTn-i

(2)

其中ν为气缸内气体物质的量,R为普适气体常量. 在各个平衡态, 活塞受到气缸内气体的压力, 外部大气压和砝码的压力保持静止, 由力学平衡条件可得

pn-iS=p0S+(n-i)mg

(3)

在中间过程的各个平衡态之间气缸内的气体处于非平衡态, 没有统一的压强, 但活塞受到的外部压力是恒定的, 气体的内能变化量可以通过外界功来计算[6]. 因为从一个平衡态到另一个平衡态的过程中，活塞的高度由hn+1-i上升到hn-i, 同时活塞受到的外部压力为p0S+(n-i)mg, 因此,这一过程中外界对气体做功为

Wi=-[p0S+(n-i)mg](hn-i-hn+1-i)

(4)

而气缸内的气体和外界没有热交换, 所以，外界对气体做功等于气体内能的增量

νCVTn-i=νCVTn+1-i-[p0S+

(n-i)mg](hn-i-hn+1-i)

(5)

联立式(2)、(3)和(5)可以得到递推关系

(6)

定义无量纲数

则式(6)可以写作

(7)

(8)

当Mg=(b-1)p0S时有

(9)

将式(7)、(9)代入式(8)可得

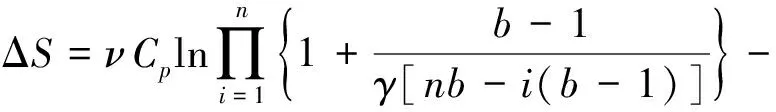
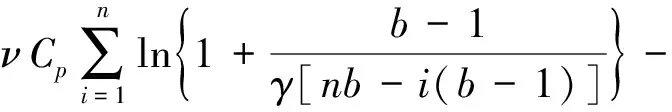
(10)

式(10)即整个过程的熵变表达式, 为n的减函数. 下面计算n→∞时的熵变, 在这一条件下对数函数中的第二项是趋于零的, 因此,可以忽略对数函数幂级数展开式中的高阶小量, 即做ln(1+x)～x的代换, 这样得到

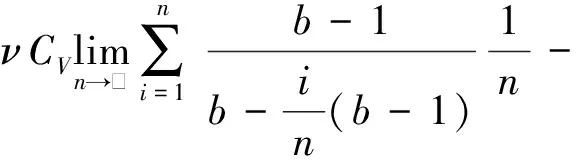
(11)

利用定积分的定义可得

νCVlnb-νCVlnb=0

(12)

因此, 在n→时,该过程确实是趋于准静态的. 同样是状态参量经历一系列微小的改变, 为何两个系统在n→的极限下具有截然不同的性质呢? 准静态过程要求任一中间态无限地接近平衡态, 因此，体系内部以及体系和外界之间必须满足力学平衡条件, 即各处压强之差为无穷小. 如果增加小砝码分割的数量, 可以以任意精度趋近于这一要求. 而对于自由膨胀过程, 在去掉隔板的瞬间, 新增加的空间仍处于真空状态, 压强为零, 这与新增加的体积大小无关, 因此，即使n→也无法使所有中间状态都无限接近于平衡态. 同时还可以看到, 要想达到理想的准静态过程, 外界参量不能存在任何有限大的跃变, 所谓过程进行得缓慢, 不仅是对整个过程而言, 对其中的任一微小过程也应成立. 所以, 在准静态过程中, 外界参量的变化应该是足够缓慢且连续的.也就是说，将t时刻的体积V分割成许多相等的小体积Vi，在静态中，各Vi中的分子数、p及T应相同；在准静态中，各Vi中的分子数，p及T也应近似相同，所以，在气体膨胀的准静态过程中，不应移去隔板，而应缓慢将隔板外推.

参考文献

1 赵凯华,罗蔚茵.热学(第二版).北京：高等教育出版社,2005.134～135

2 施建青.大学物理学(上册).北京：高等教育出版社,2009.202～203

3 张文杰,曹阳.大学物理教程.北京：中国农业大学出版社,2009.130～131

4 祝之光.物理学(第三版).北京：高等教育出版社,2009.133～135

5 张玉民.热学(第二版).北京：科学出版社,2006.18～19

6 张学斌,张公元.关于热力学中体积功的计算.大学物理,1995,14(6)：16～18