船舶柴油机曲轴动态强度分析

，，， ，琪辉，

(1.大连海事大学 轮机工程学院，辽宁 大连 116026；2.大连海洋大学 航海与船舶工程学院，辽宁 大连 116023)

随着造船工业的发展，柴油机尺寸越来越大，使得曲轴的工作条件愈来愈恶劣，曲轴的强度计算是柴油机设计中的一个关键问题。如何得到准确的曲轴应力分布、固有频率和模态振型，对改善其结构设计具有重要的理论意义[1-3]。此外，在航行中可能会出现由于船体变形等原因造成较大的船舶应力和附加弯曲应力。突变的扭转振动会影响船舶柴油机曲轴的扭转应力，导致曲轴最终的疲劳断裂[4-5]。本文以船舶柴油机整个系统为研究对象，结合AVL EXCITE多体动力学与ANSYS有限元法对船舶柴油机额定工况下曲轴进行动态特性分析，充分考虑整个船舶柴油机各个部件间的相互作用，即克服传统算法中边界条件不够准确的弊端，深入考虑曲轴上油孔和圆角等细小结构，使模型的精确性更加接近曲轴在工作状态中的实际条件。

1 AVL EXCITE多体动力学理论基础

AVL EXCITE多体动力学中用3个坐标系来构建系统模型：①全局坐标系(X,Y,Z)，用于描述各弹性体在系统中的全局运动，此坐标系为静止坐标系；②随动坐标系(X′,Y′,Z′)，即随各体一起运动；③子坐标系(X″,Y″,Z″)，即子结构ai的坐标系。图1为系统中弹性体子结构的模型。

图1 弹性体子结构的模型

子结构ai承受内力、外力及内、外力矩的作用，子结构的运动服从动量和角动量定理。子结构强迫振动方程为

(1)

式中：M——质量矩阵；

K——刚度矩阵;

gi——坐标变换产生的非线性项；

u——位移向量；

D——阻尼矩阵(刚度矩阵和质量矩阵线性组合)。

D=αM+βK

(2)

式中：α——结构阻尼的函数；

β——频率的函数。

全局中各体的运动可用角速度Ω和向量XA来表示，并应符合动量方程：

(3)

gA——坐标变换产生的非线性项;

式(3)中，角速度Ω应符合角动量方程为

(4)

式中:E、F——常量矩阵；

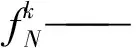
方程(4)为未封闭方程，仅当连接体传递的力与力矩均已知时，上述方程才为封闭方程。

应用上述数学模型，建立船舶柴油机系统模型进行多体动力学数值分析。将弹性体的作用力/形变作为连接体进行流体动力学分析的边界条件，而连接体的力矩/作用力成为弹性体的约束力矩/力，进行迭代计算，有效地解决了弹性体与连接体间的耦合问题。

2 模型的建立

2.1 缩减动力模型的建立

在有限元软件ANSYS中建立曲轴和主轴承的实体有限元模型，各个模型均采用solid45六面体单元，并在模型中接触位置定义主自由度节点，通过缩减程序把大幅度的自由度进行压缩，从而大大缩小了模型计算的规模，但是计算结果过程中的精度却没有受到太多影响[7]。经过缩减获得子结构各项参数文件：主自由度文件、几何文件、质量和刚度矩阵、个体(刚度)矩阵等信息。图2、3为定义过主自由度的船舶主轴承和曲轴有限元缩减模型。

图2 船舶主轴承有限元缩减模型

2.2 多体动力学模型的建立

在船舶柴油机系统全局参数中设定柴油机二冲程、转速127 r/min、发火顺序1-6-2-4-3-5、缸数6、缸径500 mm、气体压力等，该系统模型坐标系应与有限元模型坐标系保持一致。将缩减后的船舶主轴承和船舶曲轴的模型导入动力学软件AVL EXCITE中，并在EXCITE中对体单元和连接单元进行定义。考虑本文研究目标，模型中建立缸套的刚体模型，并建立空间固定点；连杆仅采用3节点模型。各结构体之间通过活塞与缸套导向、各种轴承等连接体建立非线性耦合关系。模型中，用轴向均布5排，并且每排均布48根非线性弹簧来模拟各个主轴承，见图4。各根弹簧定义的阻尼和刚度值参照轴承润滑油膜的阻尼特性和刚度特性。

图3 船舶曲轴有限元缩减模型

图4 各主轴承的弹簧支撑

气体力载荷施加在连杆小端质量节点处。图5是气体力曲线，描述柴油机转速在127 r/min，气体爆发压力峰值为15.2 MPa时，气缸压力随曲轴转角的变化规律。整个柴油机系统多体动力学模型见图6。

图5 气体力曲线

2.3 有限元恢复模型的建立

在Pro/E中建立精细的三维船舶曲轴实体模型，并将其导入ANSYS进行有限元动应力恢复计算。模型考虑了船舶曲轴上细小结构，例如：油孔、过渡圆角等。在模型整体网格划分后，又将网格进一步细化来减小由于网格划分造成的计算误差。

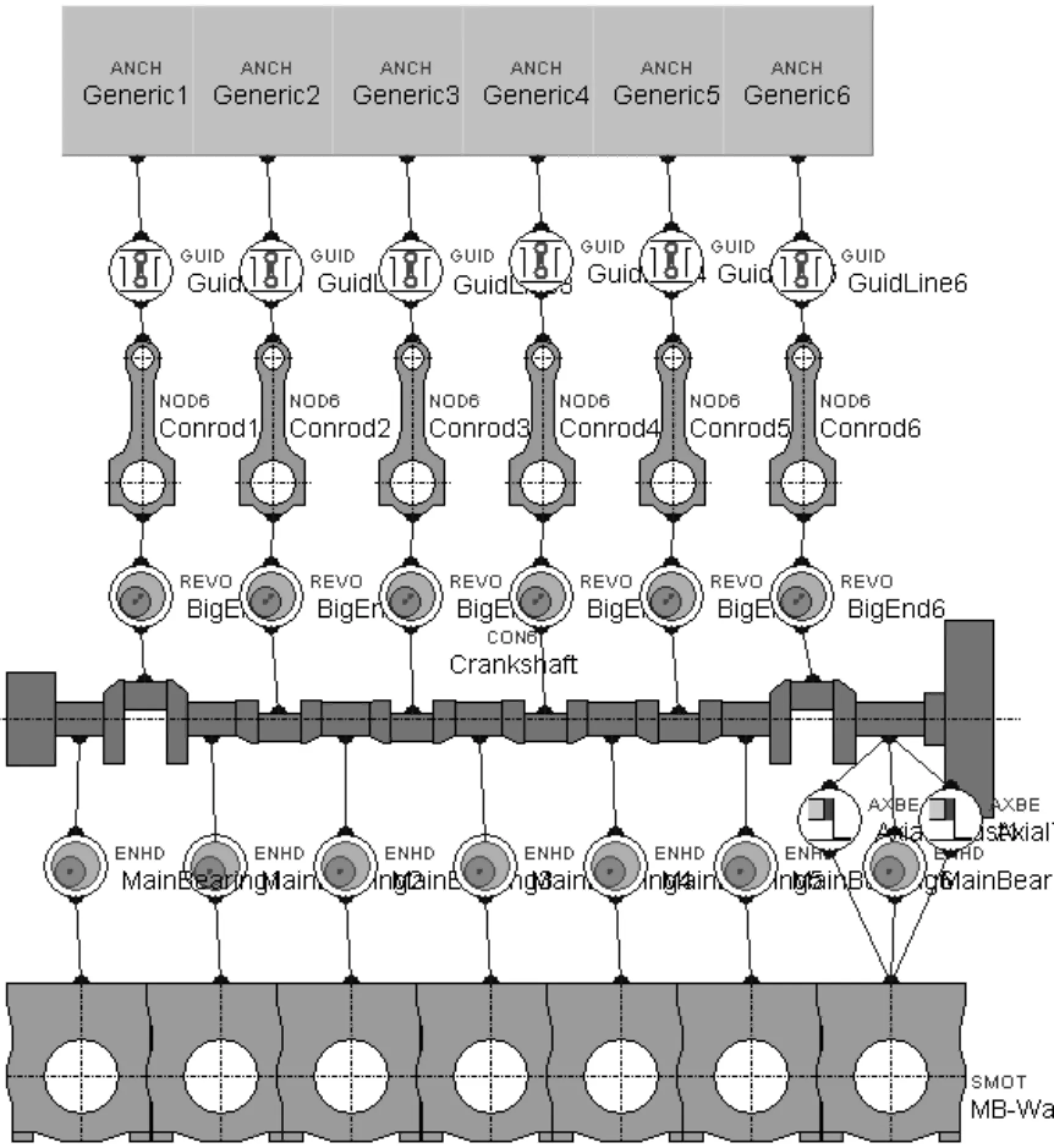
图6 柴油机系统非线性多体动力学模型

曲轴恢复模型中保留了曲轴上原有的所有主自由度，因此该模型以各主自由度节节点位移作为边界条件进行动力学计算比传统算法更加准确。图7为施加边界载荷条件进行应力恢复计算的曲轴模型。

图7 曲轴应力恢复模型

3 正常工况计算结果分析

3.1 多体动力学计算结果分析

船舶柴油机在额定工作状态下，用上述模型进行船舶曲轴动力学计算，得到各曲柄销受力、曲轴主自由度节点位移、曲轴转速脉动等参数。各曲柄销在360°曲轴转角内的受力见图8。

图8 各曲柄销受力曲线

从图8中不难看出在水平方向各曲柄销受力较为均匀，在垂直方向，仅当气缸做功时，各曲柄销受力才有波动，当对应缸发火燃烧时，受到爆发压力的影响，该曲轴销载荷相对较大，而且此时垂直方向的载荷比较大，曲轴受压严重，这与曲轴实际工况下载荷状态相吻合。

通过分析曲轴角速度、节点位移以及角加速度能够较为准确地体现曲轴的工作状况，更有利于分析曲轴变形和振动模态。由图9可以看出，曲轴在3个自由度(UX、UY、UZ)方向上的总位移值并不大，最大值为1.78 mm，动态特性较好，对于船舶曲轴而言，位移纵向值远小于横向值，这也与柴油机实际运行工况吻合，认为仿真结果可以接受。

图9 曲轴节点位移曲线

3.2 曲轴动应力计算结果分析

曲轴动态应力计算包括一个完整的曲轴工作循环，将360°曲轴转角为一个工作循环，以5°曲轴转角为标准，均分成72个时间步长，即每 5°曲轴转角进行一次应力数据恢复计算。得到曲轴最大应力值见表1。

表1 各曲拐应力大小及位置

图10 曲轴最大应力云图

由图10可以看出，在轴颈的过渡圆角处各曲拐均出现了最大应力，这是因为不管是在主轴颈过渡圆角或是连杆颈过渡圆角，局部结构尺寸均比较小，应力集中更加严重。因为曲轴输出端因带外部负载而导致自身载荷较大，造成从自由端到输出端，过渡圆角处应力值有增大的趋势。

4 结论

1)通过多体动力学和三维实体有限元结合的方法对船舶曲轴进行动态特性计算，结果表明在柴油机额定工况下，各曲拐最大应力均发生在各轴颈过渡圆角处，且计算精度更加精确。

2)本文建立了整体船舶柴油机多体动力学模型，克服了单体模型计算分析时边界载荷条件不够准确的弊端。更精确地分析了船舶曲轴在运转工况下的动态力学响应特性，也更符合船舶曲轴工作时的实际条件。

[1] 杨万里，许 敏，潘影影,等.发动机曲轴系统动力学数值模拟研究[J].内燃机工程,2006,27(1)：45-47.

[2] 陈 亮,宋希庚,明章杰,等.基于有限元和多体动力学的柴油机曲轴动态强度与冲击响应分析[J].振动与冲击,2008,27(11)：186-189

[3] 段树林,王洪伟,武占华.基于非线性多体动力学和有限元法的柴油机曲轴动态强度分析[J].大连海事大学学报,2009,35(1)：103-106.

[4] 廖建彬,蔡振雄.船舶柴油机曲轴断裂失效分析[J].船舶工程，2007,(29)：108-112.

[5] 孙连科,唐 斌,薛冬新，等.6110柴油机曲轴的三维有限元分析[J].车用发动机，2007,(2)：81-84.

[6] MOURELATOS Z P.A crankshaft system model for structural dynamic analysis of internal combustion engines[J].Computers&Structures,2001,79(20-21)：2009-2027.

[7] 于洪亮,孟宪松,段树林，等.基于多体动力学的船舶柴油机主轴承润滑特性[J].大连海事大学学报,2009,35(4)：94-98.