基于FRIENDSHIP的球艏参数化实现方法

(中国舰船研究设计中心，武汉 430064)

通常，球艏的设计是针对具体的船型，根据一些基本规律和经验确定球艏设计方案，再通过多次的模型试验来改进球艏形状来最后确定其形式。所以球艏的设计过程非常烦琐，且修改量大，效率不高。因此如何快速生成球艏形状并便于修改是亟待解决的一个重要问题。

从有利于阻力性能分析与优化的角度来进行球艏的参数化设计，可以获得更加优良的球艏型线，FRIENDSHIP Framework系统(以下简称FRIENDSHIP)为球艏乃至舰船船型的快速设计提供了一种高效、实用的方法。

1 FRIENDSHIP参数化思想

1.1 参数化建模方法

参数化建模方法有3种：①传统建模；②半参数化建模；③全参数化建模。

在这3种建模方法中，全参数化建模效率最高、经济性最佳。在FRIENDSHIP中，提供了以上3种建模方法，本文介绍的球艏参数化是全参数化建模方法，将球艏设计所涉及的特征、参数和主要要素结合起来，建立全参数化的船体曲面模型，以支持后续的性能计算和优化工作。

FRIENDSHIP参数化方法的基本思想是基于Feature建模和仿真驱动设计，建立形状特征曲线和特征参数，然后利用其内部的curve engine(曲线生成器)和meta surface(曲面生成器)快速生成船体曲面，由于船型设计主要围绕形状特征曲线和特征参数进行，因此主要任务是设计形状特征曲线和特征参数，以达到参数化设计的目标。

1.2 参数化设计过程

球艏参数化设计首先设计合理的特征参数、光顺的纵向特征曲线和典型横剖面曲线，进而生成一系列光顺的横剖面曲线，最后生成光顺的船体曲面。无论是纵向特征曲线的设计，还是横剖面曲线的建模，参数化设计的实质都是通过应变能最小原理生成满足诸如面积、形心、曲线的起点或终点的坐标、斜率、曲率等特定几何特征参数的、光顺的曲线。

球艏的参数化设计是在数学船型设计的纵向函数法的基础上继承发展而来的。与传统的设计、纵向函数法类似，首先生成横剖面面积曲线，设计水线、中纵剖面轮廓线等纵向特征曲线，再生成一系列的横剖面曲线。

2 形状特征曲线与特征参数

2.1 形状特征曲线

球艏的三维形状由球艏的边界线来确定，主要由纵向特征边界曲线、横剖面曲线、球艏域函数曲线形状来决定，见图1。

1)纵向特征边界曲线。纵向特征边界曲线，是沿船长方向的、生成横剖面曲线、球艏曲面所必须的曲线，是最主要的曲线。主要包括中纵剖线up curve和low curve，横向边界线(即球艏各剖面最大宽度处的型值点连接起来的一条空间曲线)。为便于实现，将横向边界线表达成两条平面曲线，即halfbeam curve(代表方向)和beamElevation curve(代表宽度)。

2)横剖面曲线。横剖面形状决定着球艏体积的纵向分布。艏柱处的横剖面形状可根据剖面面积与形心的位置来进行控制，在本文中命名为section curve。

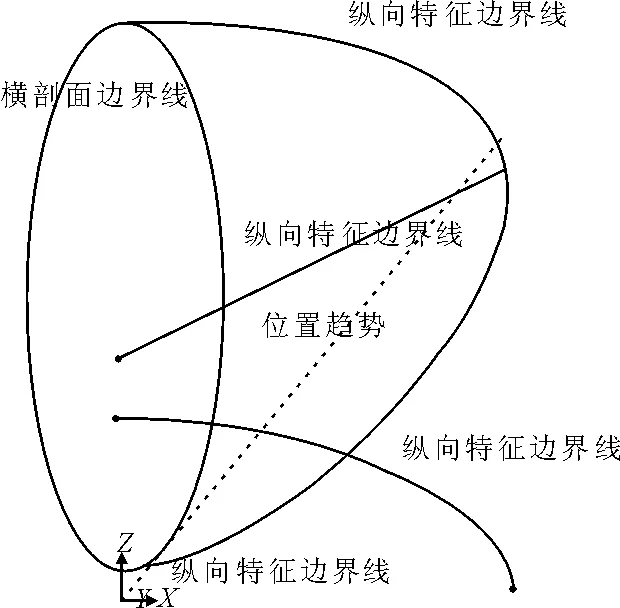
图1 形状特征曲线

3)球艏域函数(位置趋势函数)曲线。主要是参数化球艏的位置变化趋势曲线，在本文中命名为domain curve。

形状特征曲线的建模在FRIENDSHIP中使用了FSpline和Generic。

FSpline是Friendship中一种光顺建模曲线。在指定的2维基准面中，用户只需给定起始位置和中止位置以及相应的切角，同时还可以指定曲线的面积和质心的位置。这种曲线类型是高度参数化的曲线，其可编辑参数能够由函数分布来描述以用于曲面设计。

Generic曲线是一种泛型曲线，可以指定任意的x、y和z坐标。这些定义必须以曲线参数“t”来进行约束，t的取值范围为0～1。在本文中位置趋势曲线由Generic来创建。

2.2 形状特征参数

在球艏参数化设计中，形状特征参数决定了所设计球艏的纵向特征边界曲线、横剖面曲线，并最终决定球艏外形，直接影响船舶设计的质量，因此形状特征参数的确定至关重要。形状特征参数见表1。

3 球艏参数化模型

3.1 形状特征曲线实现

1)纵向特征边界曲线和球艏域函数曲线的实现见表2所列。

表2 纵向特征边界曲线和球艏域函数曲线的实现

2)横剖面曲线。在FRIENDSHIP中横剖面曲线的建立使用了Feature建模技术。根据常规定义，Feature建模可被视为几何建模的拓展，它不仅具有几何信息，在同一项中还存储了关联函数信息。Feature是高级功能，能够提供成型的参数化单元，这与现在的点、线和面的构成方法不同，比如Bezier曲线或者Coons面，除了可以生成几何体和单元，Feature还能实现特殊的工作流程。

在建模环境中使用Feature可将完整的设计任务和重复步骤融入到一个独立的项中。首先，这能完善项目结构，还可以重复只用先前定义的Feature库。这样就能在设计流程中为用户提供支持，实现更高级的用户和模型系统之间的交流。最后，可重复利用性是在设计流程中节约大量时间的关键。因为要预见用户需求的设计特征十分困难，在系统中随时引入新的特征就非常重要。用户可以定义、存储和整理自己创建的Feature。

FRIENGSHIP中，Feature还可作为特殊曲面类型meta surface的基础。曲面任何方向的截面都可以在Feature定义中进行拓扑描述。通过curve engine功能可以创建参数化曲线用来描述该截面输出参数沿曲面的分部，并连接Feature定义。通过curve engine，根据Feature中存储的模板在基线范围内任意生成截面，然后meta surface会在给定域中调用curve engine，于是获得每个曲面的截面形状，得出关于曲面的完整数学描述，不需要插值。光顺的基线和截面生成关顺的曲面，无需进一步手动关顺。此外，该曲面描述完全采用参数，所以能很好地适应系统性变形。

横剖面曲线的设计与形状特征参数、纵向特征边界曲线密切关联，也就是说横剖面曲线的设计受形状特征参数、纵向特征边界曲线的控制(横剖面曲线的主要节点、位置向量、连续性等要与形状特征参数、纵向特征边界曲线一致)。在本文中，横剖面曲线比较规则，主要分为四段，包括uppflat、upp、low和lowflat见图2。

Uppflat和lowflat是由两点创建的直线段，一般用FRIENDSHIP的“LINE”来创建；upp、low是由两点创建的平面曲线，曲线的形状是与Uppflat、lowflat相切的，一般用FRIENDSHIP的“fsplinecurve”来创建，此外，除了在首末两端的切向进行控制外，还对其面积进行了控制，设定了控制参数——丰满度“fullness”，通过面积对曲线的形状进行控制。

图2 横剖面曲线生成示例

以上创建由Feature Definition完成，具体如下。

1)输入项(argument)。输入项是实现横剖面曲线创建的数据源，在输入项中体现设计者的设计思路和参数入口，此外，输入项还对应曲线引擎“Curve Engine”的驱动配置信息。

2)程序实现(create Function)。在确定了输入项后，就可以进行横剖面曲线的程序设计，这一部分中主要是调用FRIENDSHIP的系统函数(FRIENDSHIP系统中提供了大量的系统函数，包括各种实体的建模、属性和配置)实现横剖面曲线的建立。

3)输出项(attribute)。在完成了程序实现后,系统在输出选项 “Attribute” 中系统可以自动生成输出参数，设计者根据需要可有针对性地选择需要输出的内容。

4)关联关系。为了说明输入项、程序实现、输出项以及横剖线具体样式之间的关系，在图3中用框图的形式进行了详细描绘，并刻画了其中的参数对应关系。

3.2 各站横剖面线生成

以上只是建立了一条横剖面曲线的生成方式，在船舶设计中要用到一组沿纵向曲线从前到后的横剖面曲线，所以还要有生成其它站线的横剖面曲线的机制和方式。

其它站线的横剖面曲线具体实现方式是通过curve engine来实现的。

1)在 curve engine界面(见图4b)中，首先要定义基线“base curve”，基线主要是指横剖面曲线，在“Base Curve”加载横剖面曲线“section”。

2)选择坐标平面，主要是指明纵向曲线的趋势方向平面，在本例中为Y-(XZ)。

图3 Feature definition各项逻辑关系

3)curve engine中实现横剖面曲线输入项(argument)与纵向曲线的对应关系，具体见图4。

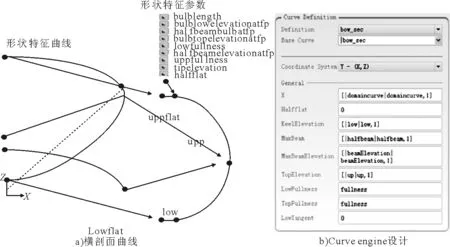
图4 各站横剖面曲线生成逻辑关系图和Curve Engine界面

3.3 曲面生成

在已经建立各站横剖面曲线以后，就可以依据蒙皮法建立曲面。在FRIENDSHIP中实现的方式是meta surface。meta surface译为元曲面，其基本原理是将横剖面曲线融合在一起生成曲面的过程。多数情况下，横剖面曲线的蒙皮都会产生满意的结果，但在过渡的地方也有例外情况出现，为此FRIENDSHIP中引入了优化处理机制。

meta surface曲面的建立如图5和6。①确定曲面的过渡方式，在本例中选择“smooth endings”；②确定meta surface的起止位置和引擎，在本例中，首端点为“0”，末端点为“bulblength”，驱动引擎(Engine)为上面建立CurveEngine“forebulb”。

3.4 静水力基本计算

在完成了曲面参数化的工作以后，就可以在FRIENDSHIP中进行设置和静水力的相关计算，此外，还可以与其它商业计算分析软件结合，进行性能分析与优化。

图5 Meta surface开发界面

图6 Meta surface结果

4 结论

FRIENDSHIP为球艏的参数化设计提供了高效、实用和可行的方法和实现机制。FRIENDSHIP系统的核心是基于设计特征(Feature)的建模，Feature建模可被视为几何建模的拓展，它不仅具有几何信息，在同一项中还存储了关联函数信息，曲面任何方向的截面都可以在Feature定义中进行拓扑描述。通过曲线引擎功能可以创建参数化曲线用来描述该截面输出参数沿曲面的分部，并连接Feature定义，然后Meta surface会在给定域中调用Curve engine，于是获得每个曲面的截面形状，得出关于曲面的完整数学描述。通过实际应用，基于FRIENDSHIP系统的球艏参数化设计效果良好。对于该方法只是尝试了基本的应用，关于球艏的水动力性能，有待进一步研究。

[1] HARRIES S. Parametric design and hydrodynamic optimization of ship hull forms[D]. Germany:Institut für Schiffs-und Meerestechnik, Technische Universität Berlin, 1998.

[2] HARRIES S. Investigating multi-dimensional design spaces using first principle methods[C]∥Seventh International Conference On High-Performance Marine Vehicles Melbourne, Florida, USA， 2010:57-59.

[3] HARRIES S,ABT C. Parametric Curve Design Applying Fairness Criteria[C]∥International Workshop on Creating Fair and Shape-Preserving Curves and Surfaces, Network Fairshape,Berlin/Potsdam,Germany,1998:58-59.

[4] FRIENDSHIP SYSTEMS. Imaging functionality for flexible shapes[J]. The Naval Architect,RINA,2007(4):41-42.

[5] 徐俊路,陈顺怀.基于CATIA二次开发的球艏参数化设计[J].船海工程，2010，39(1)：45-46.

[6] 彭 力,陈顺怀.基于肥大型船舶球艏的参数化设计[J].船海工程,2008,37(1):29-31.