高速排水型船舶兴波波形与兴波阻力的试验与数值研究
2012-01-22,,
,,
(武汉理工大学 交通学院,武汉 430063)
高速船舶设计、制造、营运中的经济性问题(尤其是能耗问题)以及高速船舶营运引起的环境问题(如艉浪对堤岸的冲刷等)对于船舶性能提出了更高的要求。高速船舶兴波波形与兴波阻力的试验与数值预报可为船舶的性能设计及高速船艉浪引起的环境问题的评估提供重要参考资料。Fr>0.4的排水型船舶大多采用方艉,而方艉型的船舶兴波的数值计算一直是船舶流体力学中的难题之一,困难主要在于方艉流动的数学模型、边界条件及其相关数值处理[1]。为了更好地了解高速排水型船舶的兴波特性并检验数值计算方法的可行性,本文在拖曳水池中对3种不同水深条件进行横排5个波高探头的纵切波形测量试验。
1 试验设备、条件与方法
实验在武汉理工大学船舶拖曳水池进行。水池总长为132 m,池宽为10.8 m,试验水深分别为2.000 m,1.500 m,0.516 m。
拖车的主要性能指标如下。
有效运行距离:118 m;
最高车速:Vmax>7.2 m/s;
稳速范围:V=0.06~7.20 m/s;
给定精度:0.1%;
稳速精度:V≤0.5 m/s为1 mm/s,
V>0.5 m/s为0.1%;
位置控制精度:±0.5 mm;
位置显示精度:±1.0 cm;
实际速度显示精度:±1.0 mm/s。
实验所采用的阻力测量系统由一个阻力仪,一个用来放大和过滤信号的调节器和一个NI数据采集系统组成。阻力仪的最大量程为400 N。实验的波形测量系统由波高传感器和5个探头组成。5个探头的分布为第1个探头距船模中线面为80 cm,然后每隔90 cm依次放置第2~5个探头。
实验的数据采集方法为:阻力数据由阻力采集系统测得,波形测量是同时进行的,分别由各个探头将采集到的信号传输到计算机,然后通过软件处理得到输出形式为波高数据和相应的电子波形图。截取适当的波形段,对相应波形段的波高数据进行波形分析。
本文的船舶试验所采用的船型是由NPL高速圆舭型排水型系列的Model 100 A 船型仿射后得到的。其主要参数为:水线长L为4.086 m,平均吃水T为0.258 m,排水量△为190 kg,宽度B为0.454 m,湿面积S为2.323 m2,方形系数Cb为0.397。
纵切法测量示意见图1,距船体中心线yc的位置是一条纵切线,xe处是波形截断进行误差修正的位置,1~5分别为5个探头。
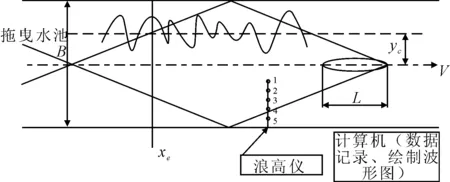
图1 纵切法测量示意
试验中采取以下措施减小误差。
1)测量前对每路浪高仪进行清零。
2)测量前对每个浪高仪都进行标定(在+25~-25 cm之间取11个点来回测量3次),并根据标定结果修正输出的波高值。
3)每一速度下的试验尽可能等待水池中波浪扰动平静后进行。
2 数值计算方法
以Rankine源法作为Green函数基本解来数值求解一般三维物体势流的数值计算。相对于Kelvin源法,Rankine源法采用的源函数简单,计算相对简单,且自动满足水底条件及无穷远处扰动衰减条件。

船体兴波问题属于无升力问题,采用常用的源汇分布法,直接在船体、自由面等边界面上布置源汇即可。基于NURBS高阶面元法与一般的低阶面元法和高阶面元法不一样,在布置源强时,不再将船体划分为一块块的面元,并在每个面元上布置源汇,而是把船体当做一整块面,其源强也是当成一整块,未知的是整个源强“面”的控制顶点,布置配置点满足边界条件,即可求出控制顶点,从而求得源强,从而解决问题。
3 实验结果与计算结果
图2给出了NPL模型在水深H=1.5 m,速度Vm=1.515 m/s时兴波波形试验中5道纵切测量波高的时历曲线,y为浪高仪距船体中心体的距离。
水深H=2.0 m时数值计算波形与实验值的比较见图3。

图2 NPL(H=1.5 m)模型兴波波形试验5道纵切测量波高时历曲线(Vm=1.515 m/s)


图3 NPL单体船船侧0.8 m处波高
当水深H=1.500 m,Frh=0.734,Vm=2.816 m/s时数值计算波形与实验值比较见图4。

图4 NPL单体船船侧y/L=0.857处波高
水深H=0.516 m(Frh=1.467,超临界速度),Vm=2.816 m/s时数值计算波形与实验值的比较见图5。


图5 NPL单体船船侧处波高
图6给出了本文由实验测得的波形计算得到的波形阻力系数、由数值模拟得到的波形计算得到的波形阻力系数、文献[2]给出的兴波阻力系数及由实验测得的总阻力系数经(1+k)法间接推得的兴波阻力系数的比较。图中所谓“1+k法推测值”是指当船模的总阻力系数由试验测得后,利用下式得到船模兴波阻力系数。
Cw=Ct-(1+k)Cf
(1)
式中:Ct——总阻力系数;
Cf——摩擦阻力系数;
Cw——兴波阻力系数;
(1+k)——形状因子,假定只与船形有关,且认为几何相似的船(1+k)是相同的,利用文献[3]中的回归公式近似估算,
(2)
在实验中浪高仪的5个探头会采集对应船侧不同位置的波高数据,可以用波形分析的纵切法算得对应的波形阻力系数。试验结果表明:不同的纵切位置对波形阻力系数大小有不可忽视的影响,本文采用了多道纵切的平均值。由于5号探头(即y=4.4 m处)距池壁很近,反射波到达过早,采集的有效信息段太短,明显影响纵切法计算的精度,故采用纵切法计算波形阻力时放弃了该探头所测得数据。

图6 不同方法得到的NPL船型(L/B=9)兴波阻力系数(或波形阻力系数)比较
4 结论
由波形分析计算的波形阻力往往比由拖曳试验结果换算所得的兴波阻力值低一些,这应该与破波现象及破波阻力有关。用本文采用的基于NURBS的广义边界元法计算的波形求得的波形阻力系数与文献[2]的结果很接近,但在高速段均低于由试验波形测量算得的波形阻力系数;试验中并未观察到很明显的破波现象,而由(1+k)法间接推得的兴波阻力系数值偏大。
采用的测量试验便于更好地了解高速排水型船舶的兴波波型及波阻,通过5道纵切波形数值计算兴波阻力。波形测量值、试验波形分析得到的波形阻力系数等与数值计算的相应结果的比较说明本文所采用的数值方法是可行的。
[1] 余学文,李世谟.关于非线性船波问题自由面边界条件的讨论[J].武汉理工大学学报:交通科学与工程版,1990(3):237-242.
[2] 赵连恩,韩端锋.高性能船舶水动力原理与设计[M].哈尔滨:哈尔滨工程大学出版社,2001.
[3] 赵成璧.船舶曲面设计现代方法与软件系统的研究[D].武汉:武汉交通科技大学,1999.
[4] DUMEZF-X, CORDIER S.Accuracy of wave pattern analysis methods in towing tanks.[C]∥Twenty-First Symposium on Naval Hydrodynamics,1997.
