两船波浪中并靠补给相对运动模型试验研究
2012-01-22,,
,,
(1.华南理工大学,广州 510640;2.海军兵种指挥学院,广州 510430;3.广州航海高等专科学校,广州 510725)
军用或民用舰船在远离大陆的海上实施集装箱等较重物资或弹药等高危物品的补给时,在很多情况下需要并靠(靠绑)补给。由于受到风浪流的影响以及两船间的水动力干扰会产生六自由度的摇荡运动,使补给船与接收舰产生相对运动,使下放中的货物与上升的船体发生碰撞,或已放落到甲板上的货物由于船体的下沉出现再次悬空的现象[1],这将对并靠补给特别是弹药等危险品补给造成严重威胁。因而,需要创新一种具有波浪补偿功能的辅助舰船并靠补给的辅助系泊系统,使并靠作业中两舰船的姿态受到一定约束。但由于并靠后的两舰船是大质量系统,使波浪补偿系统存在运动响应滞后问题,因而需要对两舰船并靠后在波浪中的相对运动特性进行研究。本文采用船模水池试验的方法,在不模拟两船之间的连接物特性的情况下,对两船波浪中并靠作业的相对运动特性进行研究,为下一步设计研究波浪补偿辅助系泊系统做基础。
1 船模水池试验
模型试验在华南理工大学港口与航道实验室中进行,港池长32 m,宽18 m,高1 m,蓄水深度为0.8 m。港池一端装有造波机,可产生二维规则波和不规则波;另一端铺有1∶7的消浪斜坡,可消除90%的反射波。
1.1 模型试验坐标系与相似准则的选定
为了正确描述两船在波浪中并靠时的相对运动,定义右旋平移坐标系Oi-XiYiZi(i=a,b):坐标原点O位于船舶的重心,X轴平行船体基线指向船艏,Z轴垂直船体水线面,该坐标不随船舶的摇荡而摇荡,Z轴始终保持竖直向上。

根据上面确定的相似原则可知,原型船和模型之间的长度和波高比尺为λ=25,周期、线速度比尺为λ0.5=5,频率比尺λ-0.5=0.2,面积和单位长度比尺为λ2=625,角度比尺为1,体积、质量和力的比尺为λ3=15 625,惯性矩的比尺为λ5。
1.2 两船并靠模型试验设置
试验采用的接收船和补给船的母型船和模型的主要参数见表1。

表1 两船的主要参数
表1中,Lpp为船垂线间长;B为型宽;LCG为纵向重心;GM为稳性高度;Zg为重心高度;▽为体积排水量。
两船并靠模型试验装置见图1。
船模的横摇、纵摇和首摇运动数据通过固定在船模上的倾角传感器测量得到;垂荡、横荡和纵荡则通过固定在船模重心处的加速度传感器测量船模的垂荡、横荡和纵荡加速度,经数据采集卡传送到计算机,再进一步处理得到。
试验中采用电容式浪高仪测量记录波浪的参数和波形。由于造波机本身的惯性影响,最初生成的几个波是不稳定的;在波形稳定条件下,采集连续有效波数不少于10个,取平均值。
1.3 试验条件和测试参数
1.3.1 水池试验条件设置如下
1)浪向,0°、30°、60°、90°;
2)波浪周期,1.20、1.42、1.77、2.43、4.24 s;
3)波高,24、36、60、92 mm。
根据本试验确定的相似准则可知,原型波浪周期对应为:6.00、7.10、8.85、12.15、21.20 s,原型波高对应为0.6、0.9、1.5、2.3 m。试验水深0.8 m,相当于原型水深20 m。
1.3.2 需要测试的主要参数
1)波浪波高;
2)两船在波浪中的运动为纵荡、横荡、垂荡、横摇、纵摇和首摇;
3)两船的相对运动。
1.4 相对运动计算公式
设定接收点在船b平移坐标系下的坐标为(xb,yb,zb),在船a平移坐标系下的坐标为(xa,ya,za)。
船b摇荡时,接收点在船b平移坐标系下的位置向量为(ζ1b+ζ5bzb+ζ6byb,ζ2b+ζ6bxb-ζ4bzb,ζ3b+ζ4byb-ζ5bxb);船a摇荡时,接收点在船a平移坐标系下的位置向量为(ζ1a+ζ5aza+ζ6aya,ζ2a+ζ6axa-ζ4aza,ζ3a+ζ4aya-ζ5axa)。
用X、Y、Z分别表示两船的相对横移、相对纵移和相对升沉,从而可得3个方向上的相对运动计算公式[3]。

图2 接收点位置示意图
(1)
Y=(ζ2b-ζ4bzb+ζ6bxb)-(ζ2a-ζ4aza+ζ6axa)
(2)
Z=(ζ3b+ζ4byb-ζ5bxb)-(ζ3a+ζ4aya-ζ5axa)
(3)
式中:下标1~6表示船舶的六自由度运动,分别为纵荡、横荡、垂荡、横摇、纵摇及首摇。
2 加速度信号的处理
试验采取接触式测量方法,将加速度传感器直接安装在接收船和补给船的重心上,测得该点的加速度,然后对加速度信号两次积分得到位移。该方法简单方便,得到的位移为绝对位移。但由于信号采集系统以及积分方法的影响,对加速度积分之后得到的位移信号精度不高,甚至不可用,因而本研究采用频谱转换法,将加速度谱转换成位移谱来得到摇荡运动幅值[4]。
频域积分的基本原理是首先将需要积分的时域信号作Fourier变换到频域内,则时域积分运算在频域就成为了Fourier分量系数的正弦、余弦积分互换,其结果再经Fourier逆变换,得到积分后的时域信号。对应于时域积分,加速度时程的一阶、二阶频域积分分别可以得到速度、运动位移。
设一个样本长度为T的时域信号x(t)经数据采集后,形成离散数据x(n)。如果在时间T内采集N个数据,则x(t)归一化的离散傅里叶变换(DFT)为
(4)
式中:n和k取为0,1,2,…,N-1。DFT采用离散傅里叶变换快速算法(FFT)。x(n)经离散傅里叶变换后得到的X(k)是一个长度为N的复数序列(频谱):
X(k)=DFT[x(n)]=
[(a0,jb0),(a2,jb2),…,(aN-1,jbN-1)]
(5)
x(n)中各谐波分量的幅值、圆频率及初相角由下式求出
(6)
根据信号叠加原理,任何周期信号都可通过若干简谐信号叠加得到。加速度信号用式(7)表示,其相应的位移用式(8)表示,两者的幅值和相位之间的关系见式(9)。
a=Aa0cos (w0t+φa0)+Aa1cos (w1t+φa1)+
…+AaN-1cos (wN-1t+φaN-1)
(7)
d=Ad0cos (w0t+φd0)+Ad1cos (w1t+φd1)+
…+AdN-1cos (wN-1t+φdN-1)
(8)
(9)
加速度信号频域二次积分的数值计算公式可概括为
(10)

(11)
式中:fd,fu——带通滤波的下限截止频率和上限截止频率;
X(k)——时域信号x(n)的傅里叶变换;
Δf——频率分辨率;
H(k)——带通滤波器的频率响应函数。
最后将获得的频域积分信号通过傅里叶逆变换转换回到时域获得位移的时域信号y(t)。
3 试验结果
在对测量数据进行分析时,按船舶试验的比尺换算到实船环境进行处理。
浪向角0°时X、Y、Z方向相对运动幅值响应随波高变化见图3~5。

图3 0°相对横移测试结果

图4 0°相对纵移测试结果

图5 0°相对升沉测试结果
浪向角15°时,X、Y、Z方向相对运动幅值响应随波高变化见图6~8。

图6 15°相对横移测试结果

图7 15°相对纵移测试结果
浪向角30°时,X、Y、Z方向相对运动幅值响应随波高变化见图9~11。

图8 15°相对升沉测试结果

图9 30°相对横移测试结果

图10 30°相对纵移测试结果

图11 30°相对升沉测试结果
浪向角60°时,X、Y、Z方向相对运动幅值响应随波高变化见图12~14。
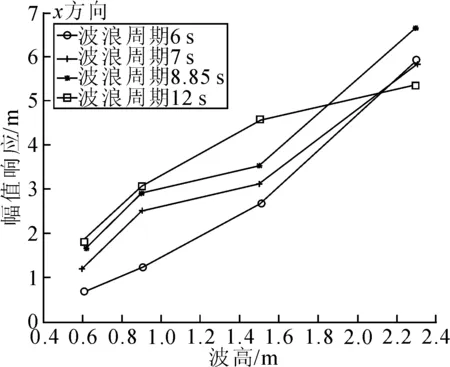
图12 60°相对横移测试结果

图13 60°相对纵移测试结果

图14 60°相对升沉测试结果
4 结论
1)在浪向角相同的情况下,3个方向的相对运动幅值响应的总体趋势都是随着波高的增大而增大;3个方向的相对运动幅值响应与波高之间的正比关系较明显。
2)相对运动幅值并不随着波浪周期的增大而增大,但在周期为8.85 s时,3个方向的相对运动在不同浪向角下几乎都要增大得快一些,这可能是该两船并靠系统的谐振周期。
3)两船相对横移和相对升沉运动的幅值显然要比相对纵移的幅值响应要大,这可能与两船间的水动力干扰对横摇、横荡和升沉运动的影响较大有关。
4)在不同的浪向角和海况下,3个方向的相对运动幅值响应基本上随着浪向角的增大而增大,但都有各自的极大值和极小值。在实施并靠补给时,应尽量选择使三个方向的相对运动幅值响应都有较合理的条件实施补给。
[1] 彭江丰.液压折臂式起重机的波浪补偿装置设计[J].船舶,2000(3):39-41.
[2] 李积德.船舶耐波性[M].哈尔滨:哈尔滨工程大学出版社,2007.
[3] 王建方.舰/舰补给系统中水动力学问题的数值仿真研究[D].哈尔滨:哈尔滨工程大学,2005.
[4] 刘继承,徐庆华,查建新.用加速度传感器测量振动位移的方法[J].现代雷达,2007,29(5):69-71.
