独塔无背索斜拉桥抖振响应时程分析

李巍峰 刘文会

（1.长春市轨道交通集团有限公司，130012，长春；2.吉林建筑工程学院交通科学与工程学院，130021，长春∥第一作者，工程师）

抖振是桥梁风致振动的一种，由脉动风诱发的抖振是一种经常性的、随机的限幅振动，如果处理不好，会使桥梁局部某些构件产生疲劳破坏，而且过大的抖振振幅也会影响行车安全和乘客的舒适性和安全性。应用谐波叠加法，模拟了独塔无背索斜拉桥——长春轻轨伊通河大桥处的脉动风场，计算得到了抖振力的时程数据，对长春轻轨伊通河大桥的抖振响应进行了时程分析，并与静力分析结果进行了对比。最后对伊通河大桥在抖振力作用下的结构安全及其使用状况作出了评价。

1 工程背景

伊通河大桥是长春市快速轨道交通环线工程跨越伊通河的独塔无背索斜拉桥。伊通河大桥主桥结构形式为混凝土塔混凝土梁，独塔无背索斜拉桥采用塔梁固结。跨径布置为31m＋44m＋130m。31 m＋44m为主塔范围，130m为主跨范围。全桥共设置18对斜索，主梁采用预应力混凝土撑梁大悬臂箱梁结构，主塔全高65m。

2 风场模拟

2.1 谐波叠加法模拟脉动风场

谐波叠加法是基于三角级数求和的频谱表示法，采用以离散谱逼近目标随机过程的模型的一种离散化数值模拟方法。该方法简单直观，数学基础严密，适用于任意指定谱特征的平稳高斯随机过程。根据Shinozuka理论，进一步计算脉动风场。采用Kaimal提出的沿高度变化的水平风速谱［1］，通过相干函数［2］计算脉动风的互相关功率谱。

取主梁（跨径130m）上的40m等间距的3个点（以主梁中点为中间点）进行脉动风场的计算机模拟。取U10＝35.4m／s［3］；空间相关系数λ取10［4］。综合考虑模拟精度及计算速度，并对比参考同类的模拟程序［5－6］，选取截断频率为4Hz，采样点数取800，时间步长取0.25s。计算得出1号点、2号点（主梁中点）、3号点的模拟风速时程曲线图（见图1、图2、图3）。

2.2 风谱验证

通过计算模拟得到的风速时程数据的模拟功率谱与目标功率谱（Kaimal谱）来验证结果的正确性。模拟功率谱与目标功率谱比较图如图4、图5、图6所示。应用功率谱估计的周期图法［7］计算模拟功率谱。

由图1、图2、图3可以看出，模拟功率谱以目标功率谱为中心上下波动，模拟谱和Kaimal谱拟合较好，说明模拟的脉动风速符合要求。

图1 1号点的风速曲线

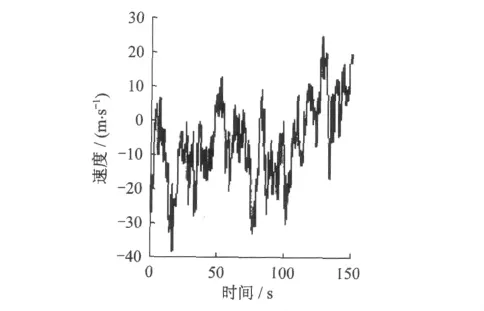
图2 2号点的风速曲线

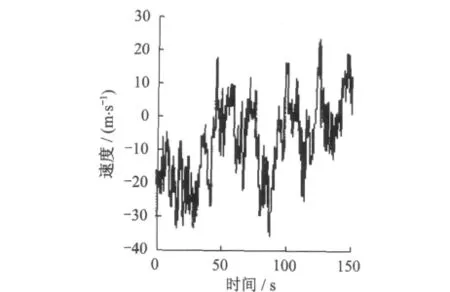
图3 3号点的风速曲线

3 抖振力的时域表达

根据准定常理论，A.G.Davenport提出抖振力时域表达式为［8］：式中：

图4 1号点的模拟功率谱与目标功率谱对比

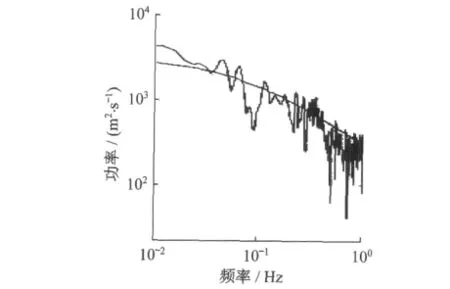
图5 2号点的模拟功率谱与目标功率谱对比

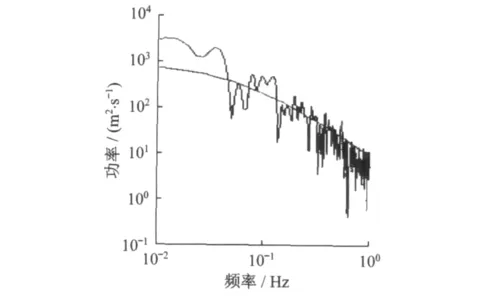
图6 3号点的模拟功率谱与目标功率谱对比

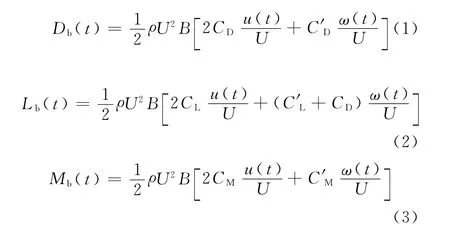
Db，Lb，Mb——抖振阻力、升力和升力矩；

ρ——空气密度；

CL，CD，CM——升力、阻力和升力矩系数；

C′L，C′D，C′M——升力、阻力和升力矩系数对攻角α的导数；

U——平均风速；

u，ω—水平向及垂直向的脉动风速。

［9］及节段模型风洞试验取0度攻角时的三分力系数CL＝0.67，CD＝1.226，CM＝0.142 5，C′L＝－1.03，C′D＝－0.25，C′M＝－0.57。

应用得到的风速时程曲线计算作用于伊通河大桥主梁的脉动风荷载。

4 抖振响应时程分析

4.1 建立有限元模型

应用大型有限元计算程序MIDAS建立伊通河大桥模型，斜拉索采为索单元，采用直杆单元进行模拟；主塔采用平面杆单元进行模拟，桥面以上塔柱根据拉索的锚固点位置来划分单元；主梁用平面杆单元进行模拟，主梁根据拉索的锚固点位置来划分单元。在主墩基础附近通过刚臂将主梁、主塔及配重梁段连接成为整体。在结构有限元模型中考虑了斜拉索的垂度效应及主塔的压弯效应。计算模型如图7所示。

图7 伊通河斜拉桥计算模型

4.2 斜拉桥的抖振时程分析

在伊通河大桥有限元模型上加载抖振力，对拉索和主梁进行抖振力时程分析。

4.2.1 斜拉索的抖振时程分析

拉索在抖振力作用下的应力时程曲线如图8。

拉索的内力变化幅值最大值与合理成桥索力值［10］对比见表1。

经过计算分析可知，在抖振力作用下，伊通河大桥拉索的内力变化幅值与合理成桥索力相比增量很小，最大不超过0.2%，在较小范围内，符合规范要求。

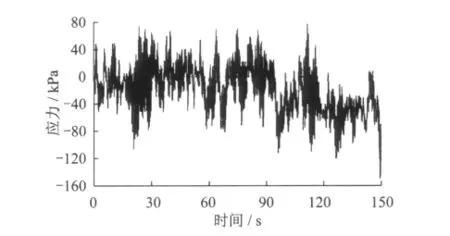
图8 A13索内力时程曲线图

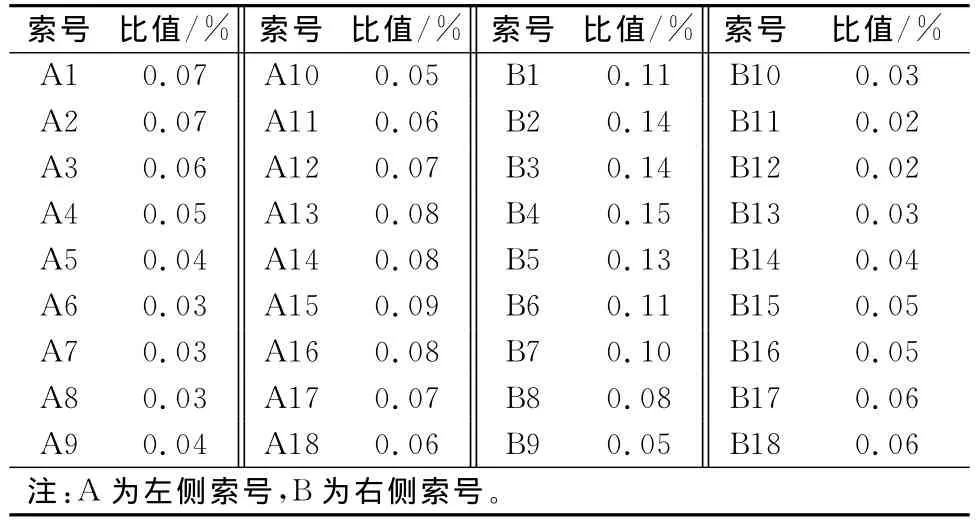
表1 伊通河大桥索力变化与合理成桥索力对比表

4.2.2 主梁的抖振时程分析

（1）主梁的抖振应力时程分析

在动力分析过程中，主梁靠近塔根处截面的应力相对较大（见图9）。

图9 主梁塔根处截面应力时程曲线图

参考文献［11］中的斜拉桥主梁静力分析结果如图10、图11所示。

图10 主梁上缘应力图

图11 主梁下缘应力图

由图10、图11可知，在静力分析中，距离110墩（主塔下沉井中心线，44m与130m跨径分界处）30m截面的应力最大，此截面的抖振力时程分析结果如图12所示。

图12 主梁距离110墩30m截面应力时程曲线图

通过计算对比主梁在动力分析和静力分析中的应力最大截面可知，伊通河大桥在抖振力作用下，主梁的应力变化幅值很小，最大不超过2%，在较小范围内，满足规范要求。

（2）主梁的抖振位移时程分析

在动力分析过程中，主梁距离110墩90m的截面位移变化幅值最大，与文献［11］中的主梁位移分析结果（见图13）对比可知，发生位移最大截面的位置基本一致。

图13 主梁竖向位移理论值与实测值对比图

主梁距离110墩90m的截面位移变化时程图如图14所示。

图14 主梁距离110墩90m截面位移时程曲线图

由图14可知，主梁的位移最大截面的振动非常小，不影响桥梁的安全及正常使用。

5 结语

以伊通河大桥为工程背景，通过编写的Matlab程序模拟了伊通河斜拉桥桥址处的脉动风场，并进一步计算了斜拉桥所受的脉动抖振力。应用大型有限元软件MIDAS建立了斜拉桥的有限元模型，对斜拉桥进行了抖振力的时程分析，得到了各根斜拉索及主梁在抖振力作用下的内力、应力及位移时程曲线图。经过动力分析并结合文献［10，11］的静力分析结果得出结论：长春市伊通河轻轨斜拉桥在抖振力作用下，斜拉索和主梁的内力及位移变化的幅值均在较小范围内，满足规范要求，不影响桥梁的安全及正常使用。

参考文献

［1］ Kaimal J C.eec.Spectral characteristics of surface layer turbulence［J］.J Royal Meteoroid Soc，1972（98）：563.

［2］ Davenport A G.The spectral of horizontal gustiness near the ground in high winds［J］.J Royal Meterol Soc，1961（87）：194.

［3］ JTG／T D60－01—2004公路桥梁抗风设计规范［S］.

［4］ 埃米尔·希缪，罗伯特·H·斯坎伦著.风对结构的作用——风工程导论［M］.刘尚培，项海帆，谢霁明，译.上海：同济大学出版社，1992.

［5］ 白泉，朱浮生，康玉梅.风速时程数值模拟研究［J］.辽宁科技学院学报，2006，3，8（1）：1.

［6］ 曹映泓，项海帆，周颖.大跨度桥梁随机风场的模拟［J］.土木工程学报，1998，6，31（3）：72.

［7］ 丛玉良，王宏志.数字信号处理原理及其 MATLAB实现［M］.北京：电子工业出版社，2005.

［8］ Scanlan R H.Role of indicial function in buffering analysis of bridges［J］.Struct Eng，ASCE，1984，110（7）：1443.

［9］ 陈英俊，于希哲.风荷载计算［M］.北京：中国铁道出社，1996.

［10］ 徐建铭.斜拉桥索力测试分析［D］.长春：吉林建筑工程学院交通科学与工程学院，2007.

［11］ 王凤国.独塔无背索斜拉桥施工控制［D］.长春：吉林建筑工程学院交通科学与工程学院，2007.