AHP与三元区间数的校园安全综合评价模型

辛 乐

（淄博师范高等专科学校 初等教育系，山东 淄博 255130）

AHP与三元区间数的校园安全综合评价模型

辛 乐

（淄博师范高等专科学校 初等教育系，山东 淄博 255130）

校园安全是学校稳定和谐发展的重要保障。以高校教育教学自身的特点及其本质特征为基础，采用AHP确定评价指标体系，构建双层评价模型，并确定权重值信息；采用九级评语集，以三元区间数决策矩阵表示评价指标对语言集的从属程度，建立对校园安全的双层综合评价模型。实验结果表明，综合评价模型能客观有效地对校园安全进行科学评估。

AHP；三元区间数；校园安全；综合评价

0 引 言

校园安全是全社会治安安全、国家和谐发展的重要组成部分,是促进教育事业蓬勃发展的基础。它直接关系到众多学生能否安全、健康地成长，也是众多家庭幸福安宁的重要保证。对校园安全评价具有群体敏感性、内部复杂性、与周边的关联性和整体综合性的特点，因而在评价过程中需要全面、系统、客观地考虑校园安全问题，建立科学合理的综合评价模型[1]。

在现实生活中存在大量不确定因素，常常依靠不确定的信息来做出评判和决策，导致无法做出精确的判断。正是由于被评判的对象具有模糊性和不确定性，很难用精确的数字来表达，而使用评语集（常指一个范围）对其进行评价，最常见的就是采用区间数评价[2]。但因为校园安全问题既综合又复杂，单独使用区间数来计算难度大，处理不方便，为此在评价过程中引入层次分析法（AHP）。AHP于20世纪70年代由美国运筹学家Staaty提出，用于分析解决结构比较复杂的多目标的决策问题[3]。该方法简单实用，并能够综合专家的经验，应用广泛。将AHP与三元区间数相结合的评价方法，既能有效处理实际问题中的非线性关系，又能真实体现评价对象的模糊性和不确定性。因此，利用AHP与三元区间数相结合建立的双层综合评价模型对校园安全问题进行评价，结果更准确，操作更简单，适应性更强。

1 评价模型中评价体系和权重向量的确定

为将校园安全评价问题中错综复杂、相互联系的各种影响因素划分得条理化、层次化，以及与专家意见和分析者的客观判断结果直接而有效地结合起来，以“系统性、科学性、客观性、可测性、可比性、简明性和综合性”为选择评价因素的基本原则，同时遵循学校工作的一般规律和高校教育教学自身的特点及本质特征，归纳总结大学校园安全评价指标。将每一层次元素进行两两对比，对其重要性进行定量描述，并确定指标和权重值信息，构建双层评价体系。

1.1 双层评价体系

将组织机构U1、校园秩序管理U2、教育与服务U3、社会环境U4、突发事件应急处理U55个因素作为第一层评价因素，即目标层，下设23个第二层评价因素，即指标层（见表1）。首先将全部n个评价因素划分成k类，设U为第一层评价因素：U={U1,U2…,Uk},其中，相应权重向量为其中设Ui为第二层评价因素：Ui={ui1,ui2, …,ui其中，i=1,2,…,m，ti(t1+t2+…+tm=n)为集合的元素个数，相应权重向量，其中，

表1 校园安全评价指标体系

1.2 权重向量

一般专家或由历史（经验）数据对评价因素集采用1～9位标度法评估定量化，把从属于（或影响）上一层的每个因素的同一层诸因素进行两两对比，构成矩阵形式，即判断矩阵A[4]。

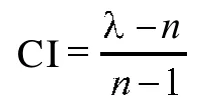
2 区间数及决策矩阵

二元区间数在自动化控制、优化决策、不确定判断、电力系统、结构设计等方面已有广泛的应用。但由于二元区间数只用上限和下限的二元表示法，有时为了覆盖整个取值范围，可能存在区间长度过大的问题。当用区间数表示一个参量时，一般默认区间数的各值取值机会均等。大多数情况下，决策者对问题的判断都有一个偏好值，此时需要对二元区间数进行修正。为解决该类型的问题，提出用三元区间数来表达决策，如t=[a,b,c]，其中b为可能性最大的取值，即为偏好判断信息。由于三元区间数能够更加细致准确地表示决策者对区间内某一属性的偏好信息和判断的不确定性和模糊性，采用三元区间数作为决策者的判断信息会更贴合现实情况，评价结果准确性会更高。

2.1 三元区间数的定义及运算

三元区间数是用三个参数表示一个区间数，记为A=[a---,a*,a+]，而a---≤a*≤a+。其中，a---表示区间的下限，称为三元区间数的小元；a+表示区间的上限，称为三元区间数的大元；a*表示在此区间中取值可能性最大的数，即信息偏好值，称为三元区间数的特元[2]。在三元区间数中，信息偏好值即特元a*在区间中出现机会最大，即a*的取值概率最大，而a*由向上限的大元a+或者向下限的小元a---取值的概率都在递减。

三元区间数的基本运算如下：

在现实决策过程中，为了能够科学合理地评价对象，决策者通常需要对同类事物的属性、准则或方案的重要性进行比较。当不能直接进行比较时，常采用决策指标与评语集两两对应比较的方式形成决策矩阵，再由决策矩阵导出其重要性的排序。

2.2 评价语言及决策矩阵

依据Xu ZS等[6]提出的模糊语言处理准则，令评语集S={一级，二级，三级，四级，五级，六级，七级，八级，九级}，其中，一级＞二级＞三级＞四级＞五级＞六级＞七级＞八级＞九级。

依据文献[2]定义三元区间数表示的九级评语如下：

其中是一个三元区间数，表示对目标U而言指标xi属于yi的程度。

3 综合评价模型

校园安全综合评价模型由以下三部分组成：一是专家根据学校实际依据第二层评价指标对9级评语集给出决策矩阵，并对目标层Ui=(i=1,2,…,k)进行评价；二是利用判别向量对校园安全进行综合评价，得到综合评价向量；三是将评价向量再转化为评价语言。

3.1 对目标层Ur=(r=1,2,…,k)的评价

将求得的判别向量Ni写成评价矩阵M，得：

利用三元区间数基本运算，将目标层的权重信息λ与评价矩阵M按照下列公式进行运算，得到学校的综合评价向量E，得：

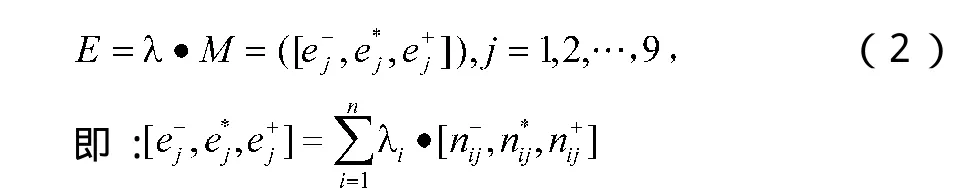
将E导入，得：

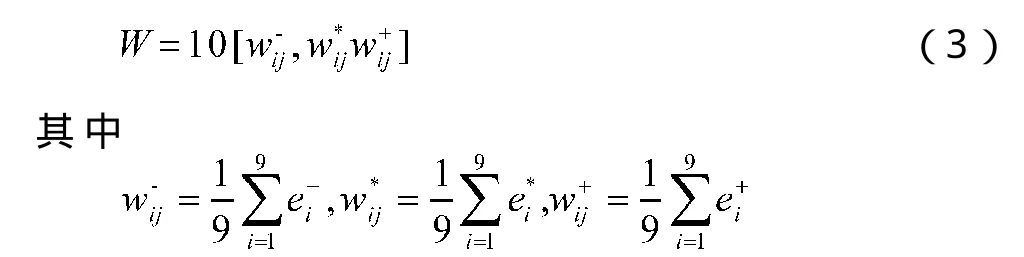
通过上述综合评价分析，得到科学合理的校园安全评价结果。为了方便决策者和参评者对评价结果的理解，需要将评价结果转化为日常使用的评语集Y。依据最大隶属度原则[7]，确定三元区间数W所属的评语，确定评价的最终结果。

3.2 综合评价模型算法

通过对以上目标层的评价，可得到综合评价模型算法步骤如下：

（1）根据实际情况确定评价体系和指标；

（2）根据层次分析结构，对评价因素集采用1～9位标度法评估定量化，构造各层次的判断矩阵，即权重判断矩阵A；

（3）利用“乘积方根法”求解判断矩阵A的最大特征值所对应的单位特征向量，并对判断矩阵进行一致性检验；

（4）依据三元区间数表示的九级评语集，确定三元区间数的决策矩阵；

（5）根据（1）式对目标层Ui=(i=1,2,…,k)的因素进行评价，根据（2）式和（3）式对校园安全进行综合评价；

（6）根据最大隶属度原则，确定三元区间数所属的评语，确定综合评价的最终结果。

4 应用实例

以淄博职业学院为例，应用综合评价模型对该校的校园安全状态进行综合评价。按照综合评价模型算法步骤进行评价。根据九级评语集，专家结合实际情况，对目标Ui=(i=1,2,…,5)给出三元区间数的决策矩阵，即：

根据（2）式可得到综合评价向量E，即：E=([0.0324,0.0342,0.036],[0.212,0.225,0.238],[0.162,0.159,0.170],[0.135,0.16,0.171],[0.0792,0.0871,0.095],[0.0331,0.0373,0.0414],0,0,0)

根据（3）式可得到最终综合判断三元区间数为：W=[0.725,0.781,0.837]。根据最大隶属度原则，确定三元区间数属于的评语集G3，确定该校的校园安全评价水平的最终结果为三级。

这说明该校园安全状态良好，且符合实际情况。从决策矩阵的结果可以看出，该校的校园安全在某些方面存在隐患，如校园秩序管理中的道路交通安全、建筑设施安全方面存在不足，消防、逃生的演练欠缺，网络安全和室内外活动伤害预防未能引起相关部门的重视。因此，该校安全领导机构应在以上方面采取积极有效的安全预防措施，以确保校园安全。

5 结 论

实验结果表明，利用综合评价模型对校园安全进行评价的结果与淄博市高校工委安全稳定工作督查组对校园安全评估的结论基本一致，符合校园的实际情况。因此，校园安全综合评价模型能更客观、科学、有效地评估校园安全，减少主观因素影响，方便高校自评自查及时了解自身安全现状，且对加强高校安全管理，有针对性地改善校园安全环境，预防重大事故的发生等都具有重要意义。

[1]刘金星.构建校园综合治理评估体系的几点思考[J].赣南师范学院学报，2004(5):119-120．

[2]胡启洲，张卫华.区间数理论的研究及其应用[M].北京:科学出版社，2010．

[3]胡运权.运筹学基础及应用[M].北京：高等教育出版社，2004．

[4]郭俊凤，田崇瑞，徐红波.基于AHP的教学质量评价体系构建[J].信息与电脑，2011(6):227-228．

[5]荆广珠，黄玉枝.新建本科院校“高等数学”精品课程建设的探索与实践[J].高等理科教育，2008(6):88-90．

[6]Xu Z S，Da Q L.Method based on fuzzy linguistic scale and FIOWGA operator for decision-making problems[J].Journal of Southeast Univercity(English Edition)，2003(19):88-91.

[7]黄丽，胡世凯，李中夫.基于标准论域确定隶属函数的方法[J].四川大学学报:自然科学版，2010(2):207-212．

Comprehensive Evaluation Model for Campus Security Based on AHP and Ternary Interval Numbers

XIN Le
(Primary Education Department, Zibo Normal College, Zibo,255130, China)

Campus security is the top priority for the steady and harmonious development of a school. Considering the characteristics of college teaching, a double-layer evaluation model was established by adopting analytic hierarchy process (AHP), and the weight value information was determined. Meanwhile, a double-layer comprehensive evaluation model for campus security was established by using nine level remarks and ternary interval numbers decision-making matrix to indicate the dependence of evaluation index on the language set. Results show that the model can make an objective and effective evaluation of campus security.

AHP; Ternary interval numbers; Campus security; Comprehensive evaluation

O221.6

A

1671-4326(2012)01-0063-05

2011-12-01

淄博师范高等专科学校青年基金（09xk005）

辛 乐（1982—），女，山东淄博人，淄博师范高等专科学校初等教育系助教，安徽大学硕士研究生.

乔维德]