李代数W[G]的自同构群与Verma模

徐崇斌

(1．温州大学数学与信息科学学院，浙江温州 325035；2．华南理工大学理学院数学系，广东广州 510640)

李代数W[G]的自同构群与Verma模

徐崇斌1,2

(1．温州大学数学与信息科学学院，浙江温州 325035；2．华南理工大学理学院数学系，广东广州 510640)

设F是特征0的域，G是它的加法子群，相应于F和群G，定义一类李代数W[G]．在本文里，李代数W[G]的自同构群与Verma模的可约性得到仔细地研究．其中自同构群的确定主要依赖于一些特殊自同构的构造，而Verma模的可约性完全取决于W[G]中元I0的作用是否为零．

李代数W[G]；自同构群；Verma模

1 李代数W[G]

众所周知，Virasoro代数是一个重要的无限维李代数，无论在数学领域，还是在物理领域都有着广泛的应用．因此，Virasoro代数自产生以来就一直是人们研究的重要对象，不仅如此，人们还研究了许多与之相关的李代数，其中具有代表性的有广义 Witt代数、广义 Virasoro代数、Heisenberg-Virasoro及广义Schrödinger-Virasoro代数等[1-4]．

2006年，M. Henlel等人在研究一类物理现象的过程中又引入了一个与Virasoro代数相关的李代数W[5]，该代数是复数域上由基生成的一个无限维李代数，它上面的李运算[⋅,⋅]定义如下：

容易看出李代数W是Witt代数与它的幂零理想的半直积．文献[6-7]对李代数W的导子代数、中心扩张及自同构群都进行了研究．受到前人工作的启发，本文定义了广义的李代数W，并对它的自同构群和Verma模进行了仔细地研究．

设F是特征0的域，G是它的加法子群．相应于子加群G，首先定义一类李代数W[G]．

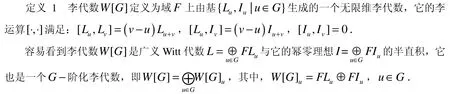
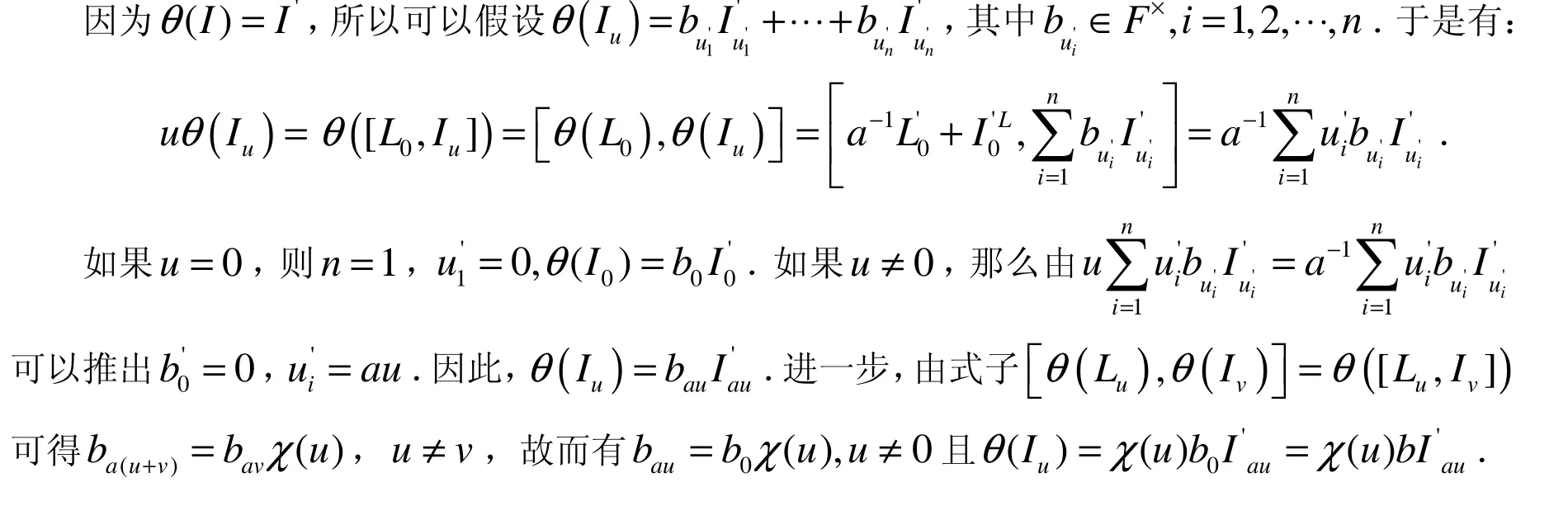
2 李代数W [ G ]的自同构群

3 李代数W[G]的Verma模

[1] Mazorchuk V. Verma module over genenralized Witt algebras [J]. Compos Math, 1999, 115: 21-25.

[2] Hu J, Wang X, Zhao K. Verma module over genenralized Virasora algebras Vir[G] [J]. J Pure Appl Alg, 2003, 177: 62-69.

[3] Gao S, Jiang C, Pei Y. Structure of the extended Schröinger-Virasoro algebras [J]. Alg Colluq, 2009, 16(4): 549-566.

[4] Tan S, Zhang X. Automorphism group and Verma module for generalized Schröinger-Virasoro algebras [J]. J Alg, 2009, 322: 1379-1394.

[5] Henkel M, Scott R, Stoimenov S, et al. The Poincaré algebra in the context of ageing systems: Lie structure, representations, Appell systems and coherent states [EB/OL]. [2011-08-08]. http://arxiv.org/abs/math-ph/0601028v1.

[6] 高寿兰, 姜翠波, 裴玉峰. 一类李代数的导子及中心扩张与自同构[J]. 数学学报, 2009, 52(2): 281-288.

[7] Zhang W, Dong C. W-algebra W(2,2) and the vertex operator algebraL(1/2,0)⊗L(1/2,0) [J]. Comm Math Phys, 2009, 285(3): 991-1004.

Automorphism Group and Verma Module for Lie AlgebraW[G]

XU Chongbin1,2
(1. College of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035; 2. Department of Mathematics, South China University of Technology, Guangzhou, China 510640)

LetFbe a field of characteristic 0, G an additive subgroup ofF. Associated toFand G , a class of Lie algebraW[G] could be defined. In this paper, the automorphism group of Lie algebraW[G] and reducibility of Verma module were investigated carefully. Results showed that the determination of automorphism group is based on constructions of some special automorphisms and the reducibility of Verma module depends on whether the action of the elementI0is zero.

Lie AlgebraW[G]; Automorphism Group; Verma Module

(编辑：王一芳)

O152.5

A

1674-3563(2012)03-0013-08

10.3875/j.issn.1674-3563.2012.03.003 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2011-09-15

徐崇斌(1977- )，男，湖北黄梅人，讲师，硕士，研究方向：代数

book=20,ebook=108