反演声波阻尼系数的简单方法

王青云，王 焕

(中国计量学院现代科技学院，浙江杭州 310018)

反演声波阻尼系数的简单方法

王青云，王 焕

(中国计量学院现代科技学院，浙江杭州 310018)

研究时间调和声波的反散射问题，利用散射波的远场模式反演阻尼边界条件中的阻尼系数.首先利用单双层位势的组合逼近散射波，然后在边界上令总体场为零，将反散射问题转化为一个最优化问题，最后给出了两个二维空间的数值例子，说明了该反演方法是简单、可行和有效的.

阻尼系数；阻尼边界条件；反演

在均匀介质中，反演阻尼边界条件的阻尼系数的时间调和的声波散射反问题可归结为一个最优化问题.对以上问题，文献[1-2]用在边界∂D内部的一个封闭曲线上的积分的单层位势逼近散射波，文献[3-5]分别用在边界∂D上积分的单层位势、双层位势和单双层位势的组合逼近散射波，然后要求总体场在边界∂D上为最小，获得最优化问题.文献[3-5]中的单双层位势是在边界∂D上积分的，总体场又是在边界∂D上为最小，此时需要利用单双层位势在边界∂D上的跳跃关系，因此会产生奇异和超奇异（Hyper-singular）积分的繁琐计算.本文借鉴文献[1-5]的思想，用在边界∂D内部的一个封闭曲线上的积分的单双层位势的组合逼近散射波，然后要求总体场在边界∂D上为最小，获得最优化问题.这种方法避免了奇异和超奇异积分的繁琐运算，一个入射波即可获得很好的反演效果.

1 方法介绍

考虑在均匀介质中传播的声波，此声波碰到一个无穷长的柱体，柱体截面是一简单有界连续区域D⊂R2，且 ∂D∈C2，母线平行于z轴，入射波ui=eikxid，d为入射角，碰到该柱体后发生散射，产生散射波us，散射波在无穷远处的数据称为“远场模式”，记为u.

∞

记总体场u=ui+us，即入射波与散射波的和，正散射问题是求u∈C2(R2D) ∩C(R2D)满足

其中，v表示边界的单位外法线方向，λ(x)∈ ∂D为声波阻尼系数，k=ω/c为波数，ω>0，c表示声速.

的解称为辐射解.

辐射条件（2）具有渐进性[6]：

1.1 反演方法

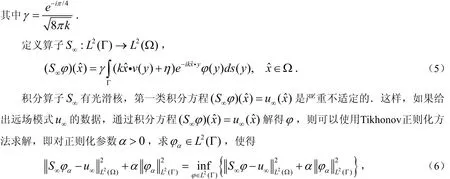
由（6）式可求得αϕ.

由（3）式获得散射波的近似值：

1.2 阻尼系数的求解

下面对前面的方法给出计算.

下面解正散射问题以获得远场模式的原始数据.采用常用的 Nystrom 方法[6]，对于定解问题：

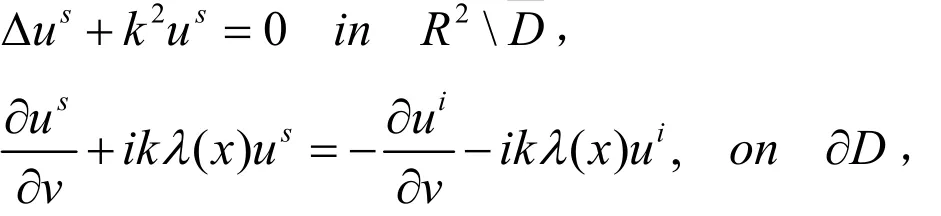
寻求如下单层位势的解：

由于散射波在边界上的跳跃关系，我们需要求解下面的积分方程：

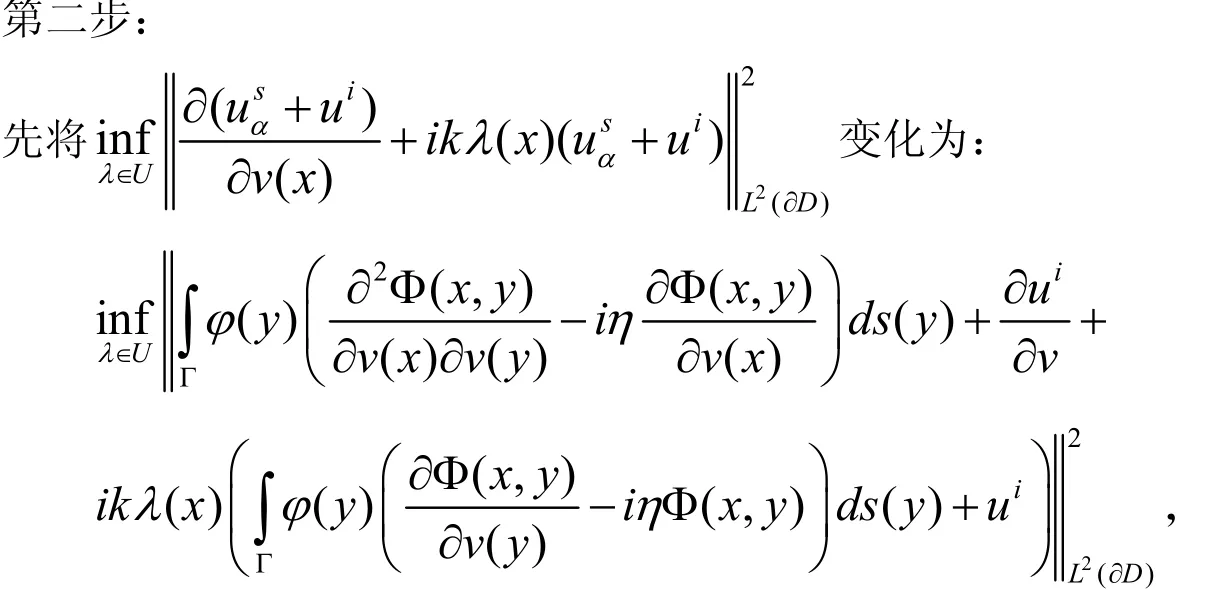
因为 Γ 是包含在∂D内的曲线，因而上式中积分核不存在奇异的情况，直接对各积分离散化就可以了.

2 数值算例

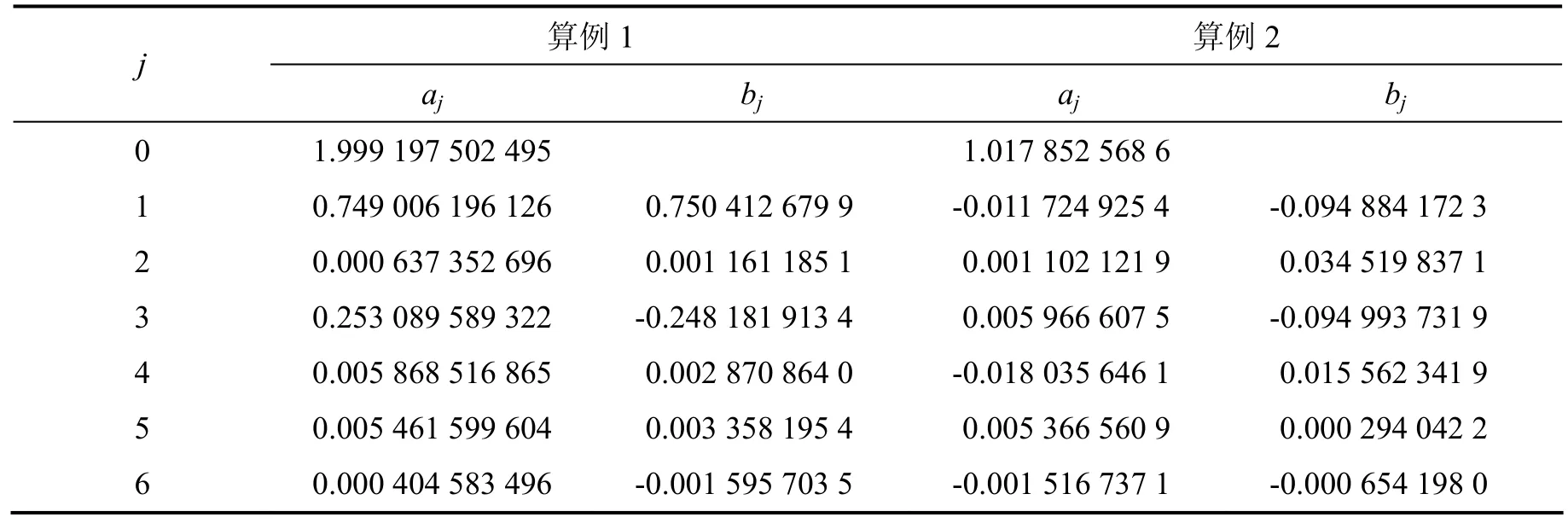
表1 算例1和算例2的反演结果

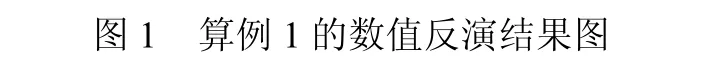
图1 算例1的数值反演结果图

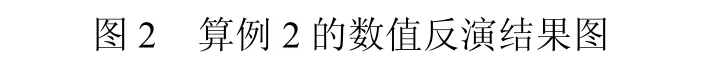
图2 算例2的数值反演结果图

3 结 论

本文讨论了已知柱体截面∂D条件下的远场模式u∞的测量数据反演阻尼系数λ(x)的反问题.首先利用单双层位势的组合逼近散射波，用Tikhonov正则化方法求解一个含有解析核的第一类Fredholm积分方程，然后利用总体场在边界∂D上等于零的条件，将以上问题转化为一个非线性方程的最优化问题，再用最小二乘法求解，得到阻尼系数λ(x)的近似解.最后给出两个常见的数值例子，从数值例子的反演结果图可以看出原始图形和反演图形完全重合，说明该反演方法是简单、可行、有效的.另外，当波数k≠1且α> 1.0E− 10时，反演效果不是很好.

[1]刘继军. 一类阻尼边界条件下的逆散射问题[J]. 计算数学, 2001, 23(1): 111-120.

[2]王连堂. 反演声波阻尼系数的一个逼近方法[J]. 计算数学, 2000, 22(3): 265-274.

[3]麦宏晏, 王连堂. 反演声波阻尼系数的一种数值解法[J]. 西北大学学报: 自然科学版, 2006, 36(2): 186-188.

[4]王枢, 王连堂. 反演声波阻尼系数的另一种方法[J]. 西北大学学报: 自然科学版, 2006, 36(5) :689-692.

[5]杨阿莉, 王连堂, 李晓华. 声波阻尼系数的反演方法[J]. 高等学校计算数学学报, 2009, 31(2): 139-147.

[6]Colton D, Kress R. Inverse Acoustic and Electromagnetic Scattering Theory [M]. New York: Springer Verlag, 1992: 37-71.

Simple Method for Inversion of Acoustic Impedance Coefficient

WANG Qingyun, WANG Huan
(College of Modern Science and Technology, China Jiliang University, Hangzhou, China 310018)

In this paper, the inverse scattering problem of time-harmonic acoustic was studied. The impedance coefficient with an impedance boundary condition was inversed by using far field pattern of scattered wave. Firstly, combined single and double-layer potential was used to approximate the scattered wave. Then the total wave was made equal to zero on the boundary, and the inverse scattering problem was transformed into an optimization problem. In the end, two numerical examples in two-dimension space were given to evidence that the method is simple, feasible and effective.

Impedance Coefficient; Impedance Boundary Condition; Inversion

(编辑：王一芳)

O29

A

1006-0375(2012)02-0016-06

10.3875/j.issn.1674-3563.2012.02.003 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2011-05-24

王青云(1978- )，女，江苏丰县人，助教，硕士，研究方向：数学物理反问题