系数含时滞的阶段结构捕食模型的稳定性
2012-01-12胡宝安刘俊峰李亚玲
胡宝安,刘俊峰,李亚玲
(军事交通学院基础部,天津 300161)
系数含时滞的阶段结构捕食模型的稳定性
胡宝安,刘俊峰,李亚玲†
(军事交通学院基础部,天津 300161)
研究一类系数含时滞的阶段结构捕食系统,分析了平衡点的局部稳定性,给出了边界平衡点(1,0)全局渐近稳定的充要条件和系统一致持续生存的充分条件,证明了正平衡点局部渐近稳定则全局渐近稳定的结论.
阶段结构捕食模型;时滞;稳定性
物种在生存过程中都要经历不同的生命阶段,因此人们将时滞引入了变量中,建立了变量含时滞但变量系数不含时滞的阶段结构模型[1].考虑到物种在不同阶段的存活率与这一阶段经历的时间长短有关这一事实,学者们建立了变量和变量系数都含有时滞的阶段结构模型[2-3].本文假设没有捕食者种群时,食饵种群服从Logistic增长规律,捕食种群分为成年和幼年两个阶段,幼年到成年的成熟期τ≥0,幼年成熟期内的死亡率γ≥0,成年捕食者的转化率依赖幼年成熟时间和死亡率,建立如下阶段结构捕食模型:
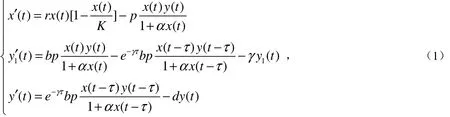
其中,x,y1,y分别表示食饵数量、捕食者幼年和成年数量,α,b,r,K,d,p为正常数.
系统(1)的第二个方程由其它两个方程决定,为了讨论方便,通过无量纲化,考虑系统:
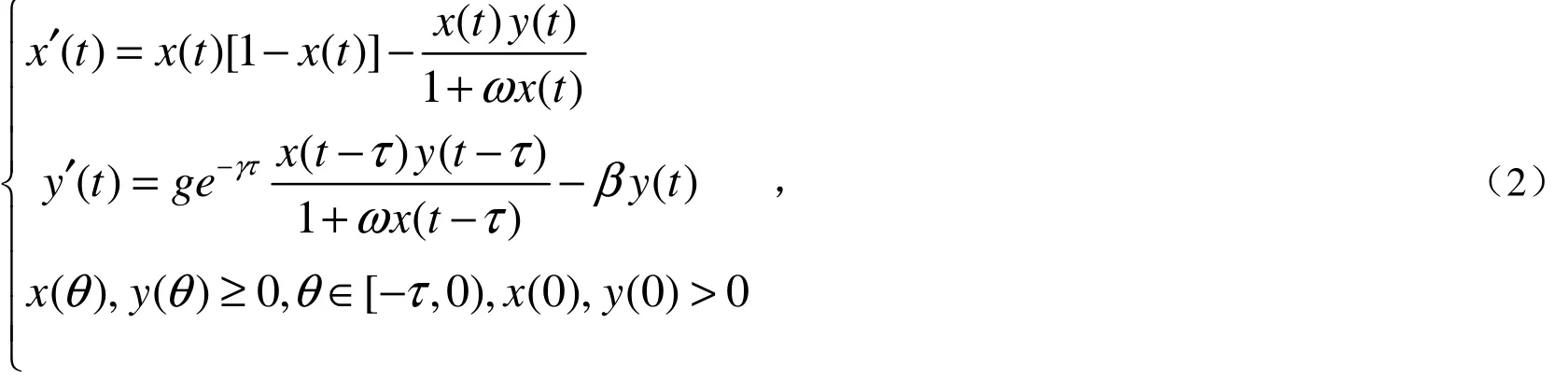
其中,g=bpK/r,β=d/r,ω=αK.容易证明系统(2)满足初始条件的解存在且恒为正.由比较定理可知系统(2)任意正解满足:


1 平衡点分析及其局部稳定性


2 平衡点(1,0)的全局稳定性
这一部分将证明ge−γτ≤β(1 +ω)是平衡点(1,0)全局渐近稳定的充要条件,其生物意义是显而易见的,即在食饵数量达到最大时,成年捕食者的转化率不超过其死亡率,捕食者种群将最终绝灭.为了证明这一结论,引入下面的引理.
引理1[5]考虑方程x′(t) =ax(t−τ) −bx(t),其中a,b,τ>0,当 −τ≤t≤0时,x(t)>0,对该方程的任意正解有:
1)如果a 2)如果a>b,则 limt→∞x(t)=+∞. 定理3 系统(2)的平衡点(1,0)全局渐近稳定的充分必要条件是ge−γτ≤β(1 +ω). 证明:由前面局部稳定性分析可知必要性成立,只需证明充分性. 由系统(2)解的恒正性可知x′(t) 定理证毕. 引理3 假设T(t)满足(16)式,且满足: 1)存在t0> 0,当t>t0时,T(t)是紧的, 2)T(t)在X中耗散, 3)T(t)是一致持续生存的, 则T(t)在X0中存在一个全局吸引子. 定理4 若ge−γτ>β(1 +ω),则系统(2)是一致持续生存的. 定理2结合引理3,有下面结论. 定理5 若ge−γτ>β(1 +ω),则系统(2)正平衡点E*全局渐近稳定的充分条件是E*是局部渐近稳定. 推论2 若ge−γτ>β(1 +ω),x0是(15)在(0,1)内的零点,则系统(2)正平衡点E*是全局渐近稳定的充分条件是x0≤x* ≤1. 下面就系统(2)中幼年成熟期的死亡率γ≠0(系统参数含时滞τ)和γ=0(系统参数不含时滞τ)相应的结果进行分析比较,从中可以看出这种含时滞参数的阶段结构模型更具有实际意义. 从正平衡点存在的条件ge−γτ>β(1 +ω)和(x*,y*)的表达式可以看到,当γ≠0时,正平衡点的存在性和值都依赖于τ.随着τ的增加,x*增加,y*减小.当τ增加到使ge−γτ=β(1 +ω)成立的τ值时,(x*,y*)就变为(1,0).根据定理 3,当τ大于等于这一值(ge−γτ≤β(1 +ω))时,正平衡点将不存在且平衡点(1,0)全局渐近稳定.而当γ=0时,正平衡点的存在性和值都和τ无关. 根据定理 5结合文献[3]的结论,对于系统(2),当γ≠0时,正平衡点在τ的有限值范围内,或者始终渐近稳定,或者经过有限次开关现象最终稳定.但当τ大于这一值时,正平衡点都将消失,捕食者种群将绝灭.当γ=0时,随着成熟时间τ的增加,正平衡点或者始终渐近稳定,或者由稳定变为不稳定(振动)并始终保持不稳定且出现一些复杂的振动现象. 这些结果一方面反映了系统(2)的解对幼年成熟期τ的敏感性,另一方面也说明了含时滞参数系统能够较好地反映现实事实.因为如果幼年成熟期τ过大,幼年个体的存活率降低,就会影响到单个成年个体的转化率ge−γτ( 1+ω)−1x.当τ增加到使成年个体的最大可能转化率ge−γτ(1+ω)−1比成年个体的死亡率β小(ge−γτ(1+ω)−1≤β)时,捕食者个体必然绝灭.但是对于γ=0,不管τ有多大,成年个体或者稳定在一定的水平,或者出现复杂的振荡现象,这与实际有些差别. [1]Wang W D, Chen L S. A Predator-prey System with Stage-structure for Predator [J]. Computers Math Applic, 1997, 8: 83-91. [2]Aiello W G, Freedman H I. A time-delay model of single species growth with stage structure [J]. Math Biosci, 1990, 101: 139-153. [3]Gourley S A, Kuang Y. A stage structured predator-prey model and its dependence on maturation delay and death rate [J]. J Math Biol, 2004, 49: 188-200. [4]Beretta E, Kuang Y. Geometric stability switch criteria in delay differential systems with delay dependent parameters [J]. Siam J Math Anal, 2002, 33: 1144-1165. [5]Xiao Y N, Chen L S. Modeling and analysis of a predator-prey model with disease in the prey [J]. Math Biosci, 2001, 171: 59-82. [6]Kuang Y. Delay Differential Equations with Applications in Population Dynamics [M]. Boston: Academic Press, 1993. Stability of Stage Structured Predator–prey Model with Delay Dependent Parameters HU Bao’an, LIU Junfeng, LI Yaling A class of stage structured predator-prey model with delay dependent parameters was studied. After local stability of equilibriums point being analyzed, accompanied by sufficient condition for system’s uniform persistence, necessary and sufficient conditions for the global asymptotical stability of the boundary equilibrium (1, 0) were given. Results showed that the locally asymptotically stable in positive equilibrium point decides the global asymptotical stability. Stage Structured Predator-prey Model; Delay; Stability (编辑:王一芳) O175.14 A 1674-3563(2012)02-0001-07 10.3875/j.issn.1674-3563.2012.02.001 本文的PDF文件可以从xuebao.wzu.edu.cn获得 2011-09-14 胡宝安(1973- ),男,河南内乡人,副教授,硕士,研究方向:常微分方程.† 通讯作者,952155382@ qq.com

3 系统的一致持续生存与正平衡点的全局稳定性



4 小 结
(General Courses Department, Military Transportation University, Tianjin, China 300161)
