充电系统可靠性的置信下限
2012-01-12杨利升郑海鹰
杨利升,郑海鹰
(温州大学数学与信息科学学院,浙江温州 325035)
充电系统可靠性的置信下限
杨利升,郑海鹰†
(温州大学数学与信息科学学院,浙江温州 325035)
利用充电设备的定时截尾寿命实验数据和转换开关的成败型实验数据,对充电系统可靠性的置信下限进行了研究.在转换开关不完全可靠的情况下,给出了充电系统可靠性的表达式,求出了充电系统可靠性的精确Fiducial置信下限,进而用拟合法和MML法分别求出了充电系统可靠性的近似置信下限,数值模拟结果说明这两种方法都是可行的.
充电系统;可靠性;置信下限
充电系统主要由充电设备、控制板、排气装置及管路系统等组成,充电系统在交通、军事等方面有着非常广泛的应用,因此,对充电系统的研究非常重要.文献[1-2]在贮备系统和转换开关完全可靠的情况下,仅对充电系统的可靠性进行了讨论.文献[3]运用WCF法与Fiducial法对指数-威布尔混合型冷贮备系统的可靠性进行了评定.文献[4]在参数相同的情况下,对指数型元件温贮备系统可靠性的Fiducial置信下限进行了研究.与前面不同,本文在参数不相同、转换开关为成败型的情况下,利用无替换定时截尾数据建立了充电系统可靠性模型,利用截尾数据与卡方分布的关系求出充电系统可靠性的精确Fiducial置信下限,并用Beta分布拟合法和MML法分别求出充电系统可靠性的近似置信下限,最后通过数值模拟说明了这种方法都是可行的,从总体上来说,用Beta分布拟合法拟合稍好于MML法.
1 基本假定
假定充电过程分为两个不同的阶段.第一阶段:两台充电设备串联工作,在t1时间内任何一台出现故障,表示第一阶段充电失败,第一阶段充电完成,进入第二阶段;第二阶段:其中一台工作,另外一台作为温贮备,在t2时间内如果工作的充电设备出现故障而贮备设备完好,贮备设备立即去替换.充电系统逐步完成以上两个阶段的充电才被看作一次成功充电.
假定 1 在初始时刻两台充电设备都是新的,第i(i= 1,2)台充电设备的工作寿命Xi和温贮备寿命Yi分别服从参数为λ和μ的指数分布,并且这两台充电设备的寿命是相互独立的.
2 充电系统可靠度的计算
2.1 第一阶段充电系统的可靠性
定理1 若随机变量X表示第一阶段充电系统的寿命,则第一阶段充电系统的可靠度为[5]:
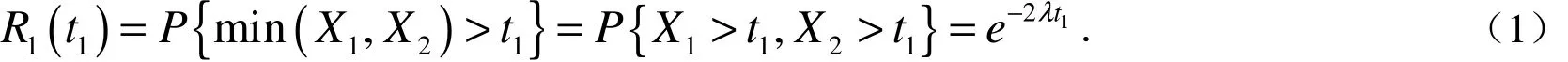
2.2 第二阶段充电系统的可靠性
第二阶段转换开关正常的概率为pk,失效的概率为qk,令P(Xk= 1)=pk,P(Xk= 0)=qk,如果随机变量Y表示第二阶段充电系统的寿命,那么Y就有如下两种情形:
情形1:转换开关正常,充电设备2的温贮备寿命小于1的工作寿命,或2的温贮备寿命大于1的工作寿命,当1出现故障时,使用转换开关,开关失效,充电系统的寿命为Y=X1.
情形2:转换开关正常,2的温贮备寿命大于1的工作寿命,充电系统的寿命为Y=X1+X2.
于是第二阶段充电系统的寿命可表示为:Y=X1+
定理2 第二阶段充电系统的可靠度为:
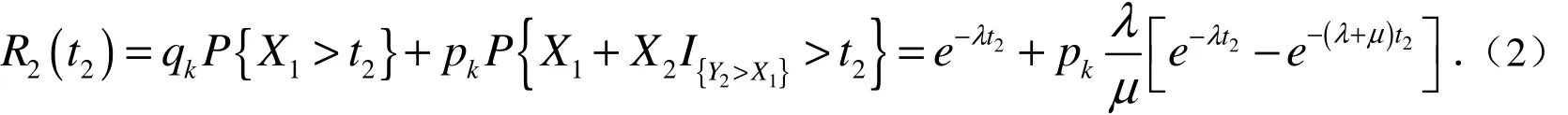
2.3 充电系统一次充电成功的可靠性
定理3 充电系统一次充电成功的可靠度为:
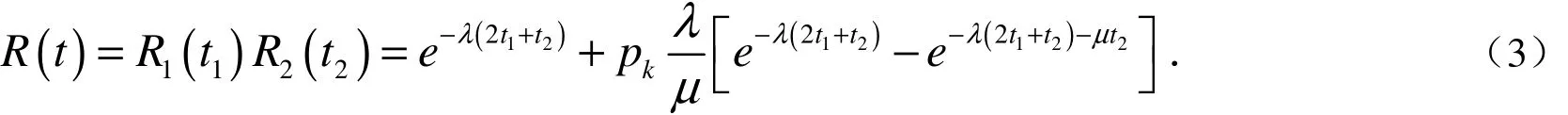
3 充电系统可靠性精确Fiducial置信下限


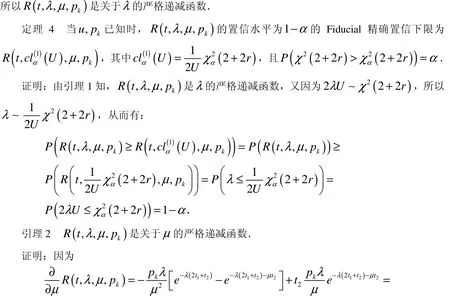


4 充电系统可靠性近似置信下限

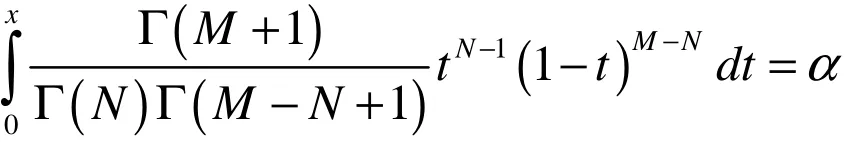
的根.由于 Beta (N,M−N+ 1)的密度函数恰好是上述被积函数,因此,可以用Beta分布来拟合Fiducial分布.另一种方法是把充电设备的指数型数据转换为充电系统的成败型数据,然后再求出充电系统可靠性的近似置信下限.
4.1 用拟合的方法求近似置信下限



4.2 用MML法求近似置信下限
为确立充电系统可靠性的近似置信下限,建立下面两个方程.
当加强筋的厚度小于塑料件的主壁厚时,其冷却速度快于主体部分,主体部分有更多的时间可以收缩,最终两者收缩差异造成塑料件翘曲变形。从分析结果(见图7)来看:加强筋厚度越接近主壁厚,对翘曲变形影响越小。
1)系统可靠性函数的极大似然估计方程:

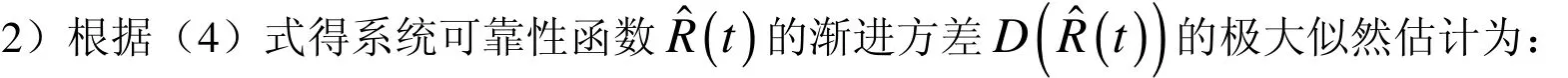

5 模拟计算
为了评价用 Beta拟合方法和 MML法所得的充电系统可靠度近似置信下限的精度,在λ,μ,pk均未知时,对充电系统近似置信下限进行模拟计算.选取以下3个指标对两种方法的优劣进行比较.
5.1 比较准则
1)覆盖率
所谓的覆盖率就是模拟中计算出的系统可靠度置信下限小于系统可靠度真值的比率,覆盖率可以近似地看作是所用评估方法的实际置信水平,它越接近预定的置信水平,该方法越好.
2)标准差
所谓标准差是指计算出的系统可靠度置信下限相对于系统可靠度真值的均方误差,它可以刻划置信下限相对于可靠度真值的离散程度.
3)γ分位点
这里的γ是预先给定的置信水平,如果模拟n次得到n个置信下限,按照置信下限的定义,这些减去系统可靠性真值后的置信下限的γ分位数与0越接近,该方法越好.
5.2 模拟步骤
第一步:给定λ,μ,pk,ti的一组值,计算出充电系统可靠性R(t)的真值.
第二步:用Matlab软件分别产生分布为 1 −eλti,1−eμt2的(m,r) ,(n,s)样本,并对给定的M产生成功概率为pk的N重贝努力试验的成功数N.
第三步:按照本文所给的两种近似方法求出原系统可靠性的近似置信下限,并重复1 000次.
5.3 模拟结果及分析
本文做了大量模拟运算,这里只列举其中的一部分,见表1.

表1 模拟计算的结果(λ = 0.01,μ = 0.002, pk = 0.8, X(0) = 20,Y(0)=20)
从表1可看出,用MML法时,相应的覆盖率和分位点都比较好,分位点在-0.004 8 – 0.000 1之间,当样本点较小时,标准差较大,当样本点在(10,20)时,标准差、分位点明显变好,当故障数为0时,会出现冒进的情况,因此MML法不适合故障为0的情况.用Beta方法,不论样本大小,相应的覆盖率都相当的好,分位点在-0.009 4 – 0.000 1之间,而且随着样本量的增加,分位点趋于0,当样本量较小时,覆盖率总是大于置信度,可以认定估计的结果是保守的,同时标准差较大,随着样本量增大,标准差明显变小.从覆盖率、分位点、标准差来看,Beta拟合法稍好于MML法.
[1]胡思贵, 赵平, 赵明. 潜艇充电系统可靠性模型[J]. 数学的实践与认识, 2009, 39(19): 98-101.
[2]赵旭, 杨子怡. 充电系统可靠性分析[J]. 数理统计与管理, 2009, 28(6): 986-993.
[3]黄宝胜, 李国英. 冷贮备系统可靠性评定的统计方法[J]. 系统科学与数学, 2005, 25(2): 204-215.
[4]郑海鹰. 两部件温贮备系统可靠性的Fiducial置信限[J]. 科学技术与工程, 2008, 8(3): 604-608.
[5]曹晋华, 程侃. 可靠性数学引论[M]. 北京: 高等教育出版社, 2006: 22-24.
[6]陈希孺. 数理统计引论[M]. 北京: 科学出版社, 1981: 358-394.
[7]赵宇, 杨军, 马小兵. 可靠性数据分析教程[M]. 北京: 北京航空航天大学出版社, 2009: 69-83.
Lower Confidence Limits of Charging System’s Reliability
YANG Lisheng, ZHENG Haiying
(College of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035)
Lower confidence limits of charging system’s reliability were studied with data of Type I censoring life test and that of switch’s pass-fail test. Then with the condition of unsafe and unreliable switch, the expression of charging system’s reliability was given to obtain the precise Fiducial lower confidence limits of charging system. Furthermore, the approximate lower confidence limits of charging system were separately obtained by method of moment fitting and that of MML. The simulation shows that the two methods are feasible.
Charging System; Reliability; Lower Confidence Limit
(编辑:王一芳)
O213.2
A
1674-3563(2012)02-0008-08
10.3875/j.issn.1674-3563.2012.02.002 本文的PDF文件可以从xuebao.wzu.edu.cn获得
2011-09-09
2010年浙江省大学生科技创新活动计划(新苗人才计划)项目(R424054)
杨利升(1985- ),男,安徽阜阳人,硕士研究生,研究方向:应用统计.† 通讯作者,wzzhying@163.com
