＊ 平面上各向异性二维格点模型的密度演化

林海，张建忠，乔文华

（包头师范学院 物理科学与技术学院，内蒙古 包头 014030）

＊平面上各向异性二维格点模型的密度演化

林海，张建忠，乔文华＊

（包头师范学院 物理科学与技术学院，内蒙古 包头 014030）

模拟了两个各向异性的二维格点模型的密度演化，并与各向同性模型进行对比.结果表明：具有无限多个吸收态的二维格点模型的密度演化受控于演化的动力学机制；不同的模型使得激活态和吸收态的存活区域不同，各向同性模型比各向异性模型更易于趋向均匀化，控制参数r对演化取向影响更明显.

各向异性模型；吸收态；激活态；密度演化

0 引言

由于非平衡态的相变，特别是具有吸收态的非平衡态的相变在生态进化、表面催化反应及介质的界面行为研究等领域有广泛的应用前景，使人们对非平衡态相变的研究不断深入.研究非平衡态相变的方法之一就是引入相应的理论模型，迄今为止，所用的理论模型有含有一个吸收态的模型，含有两个吸收态的模型［1－2］以及具有无限多个吸收态的模型［3－6］.例如Bak－Sneppen’s的物种进化模型（BS模型）就是一个简单而有趣的此类模型［2］，在这个模型中，Bak和Sneppen建议每一个物种对其所处的环境有一个适应度fi∈（0，1），在进化的每一时刻，具有最小适应度的物种将发生变异，它被一个具有随机适应度的新物种替代，而且与它最近邻的物种也受到影响，它们的适应度也被随机的选择.而Lipowski等研究了几个类似的模型［7－9］，Lipowski模型的主要思想是，一个给定物种的适应度是由它和周围物种之间的相互作用的大小来确定.在这样的模型中，如果物种的适应度低于一定的阈参量r，就称此物种处在激活态，这里r被认为是某种类型的生态学作用力，根据r的值决定模型是处在激活态还是处在非激活态（吸收态）.因为Lipowski等讨论的是一个一维的具有无限多个吸收态的模型，所以在以前的工作中，我们模拟了具有无限多个吸收态的各向同性的二维模型的密度演化和相变，并得出了一些有意义的结果［10］.然而，对于具有无限多个吸收态的各向异性二维模型的研究尚少见报道，由于许多实际问题是各向异性的，因此，本文采用蒙特卡罗（Monte Carlo）方法对平面上各向异性的二维格点模型进行分析和密度演化的计算机模拟，并将模拟结果与先前的结果进行对比分析.

1 模型简介和蒙特卡罗模拟

按照上述分析，我们考虑各向异性的具有无限多个吸收态的两相模型，建立如图1（P655）所示的层状模型，每层的正方网格的格点都有两种可能的状态（我们称之为自旋态（10））.其中格点（i，j）的自旋用Si，j表示（i，j＝0，1，2，…）.Si，j有1或0两种取值，Si，j＝1的状态称为激活态，Si，j＝0的状态称为吸收态.格点间的相互作用称为内键变量.设同一层中，每个格点只与其最近邻的四个格点发生相互作用，格点（i，j）与其最近邻的四个格点间的内键变量分别用wi－1，j、wi＋1，j、wi，j－1、wi，j＋1表示.层与层之间的每个格点，我们只考虑与其正对的上下两个格点的作用，其层间的内键变量为w.X、Y、Z轴方向的内键变量wi±1，j、wi，j±1、w的值域是不同的，此即为各向异性模型.虽然我们考虑的内键变量是三维的，但其动力学演化只模拟同一层内进行的情况.

图1 二维模型的格点结构Fig.1 Grid structure of two－dimensional mode

引入两个实参数r和s＞0，对任意格点（i，j）建立下列关系

作为模型演化的动力学机制（这里r是阈参量或称为控制参数）.具体的演化按以下方式进行：当格点（i，j）满足式（1）时，不论该格点原来处于什么状态，它都将被演变成激活态，其Si，j＝1，相应的内键变量w i－1，j、w i＋1，j、w i，j－1、w i，j＋1及w也都将在各自的值域内重新随机赋值；当格点（i，j）不满足式（1）时，不论该格点原来处于什么状态，它都将被演变成吸收态，其Si，j＝0，与其相连接的键变量均保持不变.

为了探讨不同动力学机制对演化过程的影响，我们建立了两个不同的各向异性模型，其主要差异体现在内键变量的值域上.

上述两个模型中键变量w i，j值域的选择方式，为的是保证键变量在同一层面内X，Y两个不同方向的值域不同（即w i±1，j与w i，j±1选择不同的值域，体现其各向异性的特征），以区别于各向同性模型［10］.而在模型A和模型B中，w i±1，j与w i，j±1选择不同的值域，目的是为了检测这种各向异性的强弱差异对密度演化的影响.

因为模拟只能在有限大小的模型中进行，为了消除边界效应影响，我们引进周期性边界条件，这样演化结果就与平方格点的尺度大小无关［10］，我们选取的平方格点的尺度是L＝120.当演化每遍历层间的所有格点，记作一个蒙特卡罗步长（MC），作为模拟的时间单位，在整个演化过程中s取一特定的常数.

2 模拟结果及与各向同性模型的比较

根据模拟数据我们可以作出r取不同值时的密度演化图像，即ρ－t图.模型A的演化图像如图2（P656）、图3（P656）所示，图2表示的是向激活态演化，上、中、下三条线分别对应于r＝0.011、r＝0.000 5、r＝0，图3表示的是向吸收态演化，上、中、下三条线分别对应于r＝－0.000 02、r＝－0.000 05、r＝－0.000 9.

模型B的演化图像如图4（P656）、图5（P656）所示，图4表示的是向激活态演化，上、中、下三条线分别对应于r＝0.06、r＝0.001、r＝0，图5表示的是向吸收态演化，上、中、下三条线分别对应于r＝－0.000 5、r

＝－0.000 9、r＝－0.001 5.

图2 模型A的态密度随时间的演化上、中、下三条线分别对应于r＝0.011、r＝0.000 5、r＝0）Fig.2 States density evolve over time on model A Plot ofρas a function of t for r＝0.011，0.000 5，0，（from top to the bottom）

图3 模型A的态密度随时间的演化（上、中、下三条分别对应于r＝－0.000 02、r＝－0.000 05、r＝－0.000 9）Fig.3 States density evolve over time on model A Plot ofρas a function of t for r＝－0.000 02，－0.000 05，－0.000 9，（from top to the bottom）

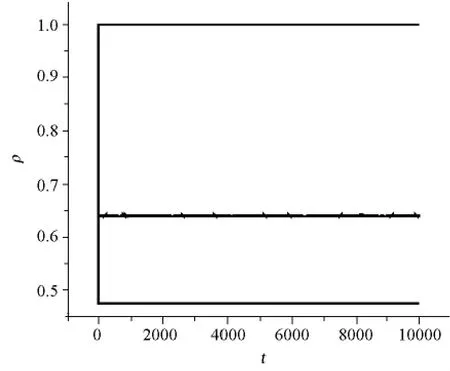
图4 模型B的态密度随时间的演化上、中、下三条线分别对应于r＝0.06、r＝0.001、r＝0）Fig.4 States density evolve over time on model B Plot ofρas a function of t for r＝0.06，0.001，0，（from top to the bottom）

图5 模型B的态密度随时间的演化（上、中、下线分别对应于r＝－0.000 5、r＝－0.000 9、r＝－0.001 5）Fig.5 States density evolve over time on model B Plot ofρas a function of t for－0.000 5，－0.000 9，－0.001 5，（from top to the bottom）

根据密度演化图像的图2和图4，我们看出系统从一个具有无限多个吸收态的初始状态演化为各格点全部处于激活态时，r的取值情况；根据密度演化图像的图3和图5，我们看出系统从一个具有无限多个吸收态的初始状态演化为格点全部处于吸收态时r的取值情况.各模型的密度演化控制参数如表1所示.

表1 各模型的密度演化控制参数的对比Table 1 Control parameters contrast for three modles

3 结论

通过对两个各向异性二维格点模型的密度演化的计算机模拟，并与各向同性二维模型模拟结果的对比，我们得出如下的结论：

（1）具有无限多个吸收态的二维格点模型的密度演化受控于演化的动力学机制，但是，尽管不同模型中的内键变量不同，在控制参数r的一定取值范围内（见表1），不同模型均可实现激活态与吸收态之间的转变.改变控制参数r的取值，可以控制格点密度演化的方向，即可演化成全部是激活态，也可以演化成全部是吸收态，还可以是激活态与吸收态两相共存.

（2）不同的模型使得激活态和吸收态的存活区域不同，对于各向异性模型只要控制参数r≥0，无论r的取值怎样小，格点不会全部进入吸收态，即系统中都有一定的激活态存在，只有控制参数r取某负值后（模型A的r＝－0.000 07，模型B的r＝－0.001 5），系统才能全部进入吸收态.而与此不同，各向同性模型中，只要r＜0时（文献［10］中给出了r＝－1×10－9时的结果），系统中的格点就全部演化为吸收态.一个自然的解释是，由于各向同性模型比各向异性模型更易于趋向均匀化，格点间的关联更强，从而控制参数r对演化取向影响更明显.

（3）尽管在我们讨论的两个不同模型中内键变量不同，但是在每个模型的两相共存区域，控制参数r都分布于r＝0两侧，随着r由正到负的逐渐减小，此时系统也逐渐由激活态向激活态和吸收态两相共存，进而再由激活态和吸收态两相共存的状态向吸收态连续过渡和演变的过程.上述情况它是否预示着一个普遍的规律，我们将会进一步地去探究.

［1］ Marro J，Dickman R.Nonequilibrium Phase Transitions in Lattice Models［M］.Cambridge University Press，Cambridge，1999.

［2］ Bak P，Sneppen K.Punctuated Equilibrium and Criticality in a Simple Model of Evolution ［J］.PhysRevLett，1993，71：4083－4086.

［3］ Jensen I.Critical Behaviors of a Surface Reaction Model with Infinitely many Absorbing Satates［J］.JPhysA：MathGen，1994，27：L61－L68.

［4］ Mendes J F F，Dickman R，Henkel M，etal.Generalized Scaling for Models with Multiple Absorbing Satates［J］.JPhys A：MathGen，1994，27：3019－3028.

［5］ Marques M C，Mendes J F F.A Parity Conserving Dimmer Model with Infinitely many Absorbing States［J］.EurPhys J，1999，B12：123－127.

［6］ Qiao W H，Fang H，He C S，etal.Critical Spreading of Active Region in a Ladder Model Possessing Infinite Absorbing States，Commun［J］.TheorPhys，2004，41：60－62.

［7］ Lipowski A，Lopata M.Model of Biological Evolution with Threshold Dynamics and Infinitely many Absorbing States［J］.PhysRev，1999，E60：1516－1519.

［8］ Lipowski A.Generic Criticality in a Model of Evolution［J］.PhysRev，2000，E62：3356－3359.

［9］ Lipowski A.Criticality in a Model with Absorbing States［J］.PhysRev，2001，E63：026105－1－026105－5.

［10］ 乔文华，张书源，陈向华，等.具有无穷多个吸收态的二维模型的密度演化［J］.内蒙古大学学报：自然科学版，2007，38（3）：263－266.

Anisotropic Density Evolution of Models of Two－dimensional Lattice in Plane

LIN Hai，ZHANG Jian－zhong，QIAO Wen－hua
（Departmentofphysics，BaotouTeacher’sCollege，InnerMongolia，Baotou014030，China）

We simulated two anisotropic density evolution models of two－dimensional lattice，and be compared with the isotropic model.The results show that the density evolution model of the two－dimensional lattice with the infinite number of absorbing states is under the control of the dynamic mechanism，and the different models makes activation states and absorption states the survival in different regions，the isotropic model is easier than the anisotropic model tend to uniformity and orientation is more obvious through the evolution of control parameterr.

anisotropy model；activated state；absorption state；density evolution

O411

A

2010－11－16；

2011－05－17

内蒙古自然科学基金（20080404 MS0108）

林海（1964－），男，副教授，主要从事计算物理的研究.＊通信联系人：乔文华（1955－），男，教授.E－mail：qwh55＠sohu.com

0253－2395（2012）04－0654－04