＊ 一类泛函微分方程正周期解的存在性

莫宜春，何志乾，王珍燕

（西北师范大学 数学与信息科学学院，甘肃 兰州 730070）

＊一类泛函微分方程正周期解的存在性

莫宜春，何志乾，王珍燕

（西北师范大学 数学与信息科学学院，甘肃 兰州 730070）

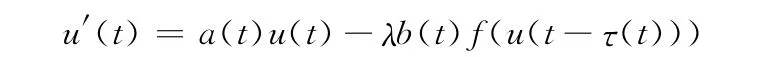
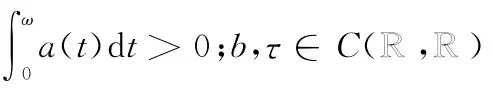
泛函微分方程；Leray－Schauder不动点定理；正周期解；时滞

0 引言及主要结果

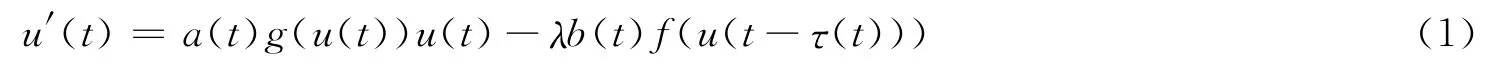
一阶泛函微分方程在生物学、人口动力学、生理学等不同的学科领域有着极其重要的应用背景.例如，观察人口密度的振荡现象，红细胞再生模型等.近年来，许多作者研究了上述泛函微分方程周期解的存在性，并获得了很多深刻而丰富的结果，见文献［1－8，9］及参考文献.

特别地，文［8］中，S.S.Cheng，G.Zhang运用 Krasnosel’skii不动点定理研究了一阶泛函微分方程

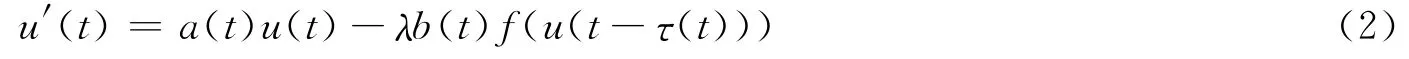
正周期解的存在性，其中λ＞0是参数，a，b，τ为连续的ω－周期函数.文［8］在非线性项f∈C（［0，∞），［0，∞））且满足条件

的假设下，获得了问题（2）正周期解的存在性.但是该文要求函数b非负.

然而，就我们所知，在函数b变号的情形下，问题（2）正周期解的存在性还没有被讨论过.鉴于此，本文在b变号的情形下运用Leray－Schauder不动点定理讨论了方程（2）正周期解的存在性，从而推广了文［8］的结果.

本文总假定

（H1）λ＞0为参数；

（H2）f∈C（［0，∞），R R）且f（0）＞0；

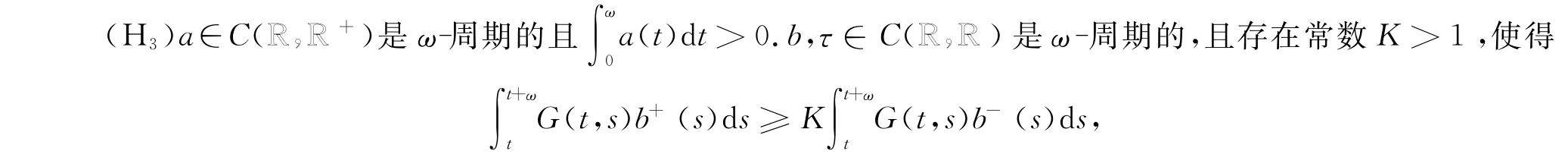
其中b＋，b－分别表示b的正部和负部.G（t，s）由（3）给出.

本文的主要工具为

引理1［10］（Leray－Schauder不动点定理）设E为Banach空间，算子A∶E→E全连续.如果集合｛‖x‖｜x∈E，x＝λAx，0＜λ＜1｝是有界的，则A在闭球T⊂E中必有不动点，其中

本文主要结果为

定理1 设（H1）－（H3）成立，则存在正数λ＊，使得当λ＜λ＊时，问题（2）至少存在一个正周期解.

1 预备知识

2 主要结果的证明

［1］ Wang H.Positive Periodic Solutions for Functional Differential Equations［J］.JDifferEqu，2004，202：354－366.

［2］ Jiang D，Wei J，Zhang B.Positive Periodic Solutions of Functional Differential Equations and Population models［J］.ElectronJDifferentialEquations，2002，71：1－13.

［3］ Jiang D Q，Wei J J.Existence of Positive Periodic Solutions of Nonautonomous Functional Differential Equations［J］.ChineseAnnMathA，1999，20（6）：715－720.

［4］ Bai D，Xu Y.Periodic Solutions of First Order Functional Differential Equations with Periodic Deviations［J］.Comput MathAppl，2007，53：1361－1366.

［5］ Zhang G，Cheng S.Positive Periodic Solutions of Nonautonomous Functional Differential Equations Depending on a Parameter［J］.AbstractApplAnal，2007，7：279－286.

［6］ Padhi S.Shilpee Srivastava，Multiple Periodic Solutions for Nonlinear first Order Functional Differential Equa－tions with Applications to Population Dynamics［J］.ApplMathComput，2008，203（1）：1－6.

［7］ Kuang Y.Global Atractivity and Periodic Solutions in Delay Differential Equations Related to Models in Physiology and Population Biology［J］.JpnJIndApplMath，1992，9：205－208.

［8］ Cheng S S，Zhang G.Existence of Positive Periodic Solutions for Non－autonomous Functional Differential Equations［J］.ElectronJDifferentialEquations，2001，59：1－8.

［9］ Jin Z，Wang H.A Note on Positive Periodic Solutions of Delayed Differential Equations［J］.ApplMathLett，2010，23：581－584.

［10］ Ma R Y.The Nonlocal Problems of Nonlinear.Ordinary Differential Equations［M］.Beijing：Science Press，2004.

［11］ Hai D D.Positive Solutions to a Class of Elliptic Boundary Value Problems［J］.JMathAnalAppl，1998，227：195－199.

Existence of Positive Periodic Solutions of a Class of Functional Differential Equations

MO Yi－chun，HE Zhi－qian，WANG Zhen－yan
（CollegeofMathematicsandInformationScience，NorthwestNormalUniversity，Lanzhou730070，China）

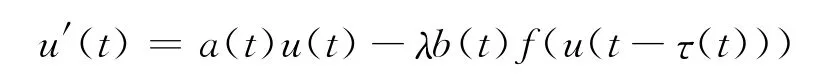
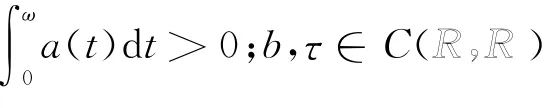
functional differential equations；Leray－Schauder fixed point theorem；positive periodic solutions；delay

O175.8

A

2011－02－27；

2011－05－25

国家自然科学基金（10671158）；甘肃省自然科学基金（3ZS051－A25－016）；NWNUKJCXGC－03－17；春辉计划（Z2004－1－62033）

莫宜春（1987－），女，甘肃定西人，主要研究方向为常微分方程边值问题.E－mail：sg25888＠163.com

0253－2395（2012）04－0591－04