＊ 双芯复合正方形格点光子晶体光纤的负色散特性

王红华，孙玉梅

（烟台南山学院 电子工程学院，山东 龙口 265713）

＊双芯复合正方形格点光子晶体光纤的负色散特性

王红华＊，孙玉梅

（烟台南山学院 电子工程学院，山东 龙口 265713）

介绍了一种双芯复合正方形格点负色散光子晶体光纤，其包层是在纯硅背景上分布着两种大小不同的按正方形格点排列的空气孔，芯区是由掺杂的高折射率材料构成.为了实现负色散，移去了包层中第三层空气孔.采用频域有限差分法对其负色散特性进行的分析表明，通过调整空气孔间距和两种空气孔的尺寸，可以得到不同程度的宽带负色散.当内芯半径取0.95μm，空气孔间距取2.05μm，大小空气孔直径分别取1.9μm、1.2μm时，可在1.55μm处实现宽带负色散，其半峰全宽超过了200 nm.这种光纤可以用于波分复用光纤通信系统中的宽带色散补偿.

光纤光学；光子晶体光纤；负色散；频域有限差分方法

0 引言

色散是光纤的一个重要参量，可使脉冲展宽，产生误码.因此在长距离的光纤通信传输系统中，必须采取色散补偿.目前，色散补偿的方法有啁啾光纤光栅（CFG）补偿法、频谱反转补偿法、预啁啾补偿法和色散补偿光纤（DCF）补偿法等［1－3］.

色散补偿光纤是一种无源器件，可放在光纤线路中的任何位置，安装灵活方便.能实现宽带色散补偿和一阶色散、二阶色散全补偿；还可与1.31μm零色散标准单模光纤兼容.适当控制色散补偿光纤的模场直径和改善连接技术，还能得到较小的插入损耗［4］.因此受到普遍重视，成为当今研究的热点.

采用双芯结构的光纤来实现色散补偿最早可追溯到1994年，当时A.J.Antos［5］等人设计了一种芯区由相对折射率差为Δp，半径为rc的折射率随半径呈抛物线分布的圆柱结构的光纤.随后，又有一些研究小组对传统双芯色散补偿光纤进行了理论和实验的研究［6－8］.

近些年，光子晶体光纤［9－10］的发展，为色散补偿光纤的制作提供了一种全新的方法.采用光子晶体光纤进行色散补偿最早可追溯到1999年，当时T.A.Birks［11］等人制作了一种横截面由规则空气孔构成的光子晶体色散补偿光纤.随后，基于双芯负色散光子晶体光纤得到了广泛研究［12－16］.然而这些结构的光纤只是单纯地追求了高负色散值，而忽视了负色散的带宽，半峰全宽少于30 nm［17］.为了克服负色散带宽小的困难，我们小组在2007年和2009年也设计了两种半峰全宽超过200 nm的光子晶体光纤，一种是复合格点的正六边形双芯结构［18］，另一种是改进的正方形格点双芯结构［19］.本着寻求带宽更宽的色散补偿光纤，我们又设计了一种双芯的复合正方形格点负色散光子晶体光纤.

1 光纤结构和计算方法

我们设计的双芯复合正方形格点光子晶体光纤的横截面结构如图1（P670）所示，包层是在纯硅背景上分布着由两种不同空气孔构成的正方形格点.其内芯为半径为r的掺锗区，折射率为1.47，外芯是移去第三层空气孔形成的纯硅环，折射率为1.45.图1中，Λ表示相邻空气孔间的中心距离，d1表示包层中大空气孔的直径，d2表示包层中小空气孔的直径.

图1 复合正方形格点光子晶体光纤的横截面Fig.1 Cross section of photonic crystal fiber with composite square lattices

采用以各向异性良匹配层（APML）作为吸收边界的全矢量频域有限差分方法（FDFD）［20－26］来分析我们提出的这种光子晶体光纤结构.采用这种方法时，只要给定光纤的几何参量和电磁参量，输入自由空间的波长，便可计算出特定波长下的传播常数β，有效模折射率neff和每个模式的场分布.光子晶体光纤的波导色散D可以由公式（1）计算出：

其中c是真空中的光速，Re代表实部，neff是有效模折射率.光子晶体光纤的材料色散由塞而迈耶尔方程［27］给出.总色散为波导色散和材料色散之和.

2 光纤的负色散特性

双芯结构的光子晶体光纤产生负色散的原因是由于这种结构的光纤支持两个超模，即基模和二阶模.当波长小于某一波长λ0时，场基本上集中在内芯传播；当波长大于λ0时，场又主要集中在外芯传播.而当波长在λ0附近时，场在内芯和外芯均有分布.这种传播现象导致了光纤的有效折射率在λ0处将发生转折，从而产生负色散.图2为该光纤内芯和外芯中传播的典型的模场图.（a）为H y场分量在内芯区的场分布，（b）为H y场分量在外芯区的场分布.

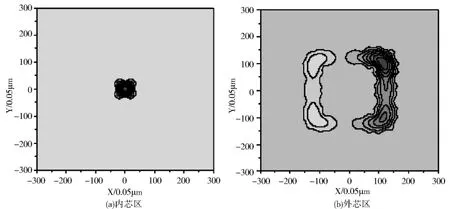
图2 Hy场的分布图 （a）内芯区 （b）外芯区Fig.2 Mode pattern of Hy field in（a）the inner core（b）the outer core

由于光纤内芯掺杂区半径的大小对色散曲线峰值所处的波长位置有直接影响，因此我们首先需要确定内芯区域的大小.图3为内芯掺杂半径与负色散的关系曲线.图中空气孔间距Λ＝1.95μm，大小空气孔直径分别为d1＝1.8μm，d2＝1.2μm，掺杂半径r从0.9μm变化到1.0μm.从图中看出，随着掺杂半径的增大，负色散的峰值点向右移动，峰值点的值有微小变化，色散曲线形状基本不变.为了与我们提出的复合六边形格点结构作一比较，也取内芯区半径为0.95μm，并在该值固定的基础上，分析负色散特性随其他三个结构参量的变化规律.

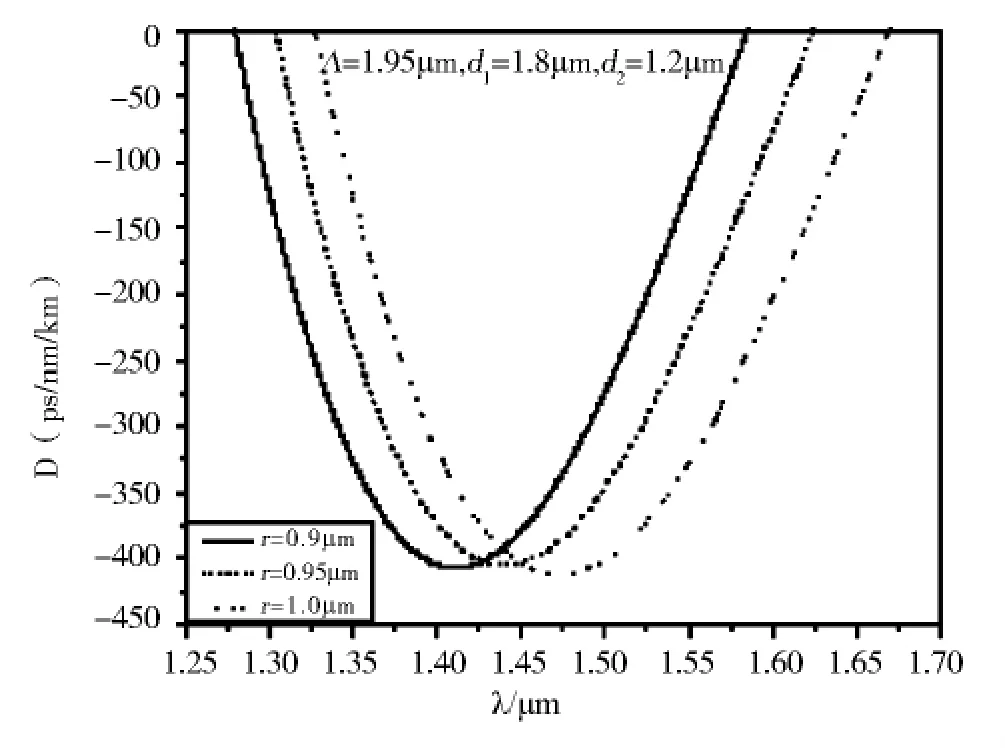
图3 内芯半径r对负色散特性的影响Fig.3 Effect of the radius of the inner core r on negative dispersion properties

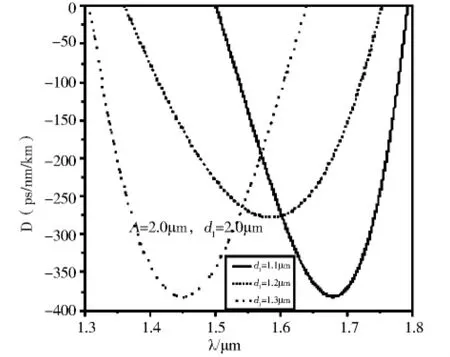
图4 当Λ＝2.0μm，d 1＝2.0μm时，d 2 对负色散的影响Fig.4 Effect of d 2 on negative dispersion properties（Λ＝2.0μm，d 1＝2.0μm）

下面讨论小空气孔直径d2对光纤负色散特性的影响.首先在给定Λ（空气孔间距）和d1（大空气孔直径）并保持它们不变的前提下，变化小空气孔直径d2，取值从1.1μm变化到1.3μm.图4、5、6分别为光纤负色散特性随小空气孔直径变化的关系曲线.从图中可以看出，随着小空气孔直径d2的增大，负色散的峰值点向左移动，并且在越靠近1.55μm处，负色散的峰值点越低，但半峰全宽在增大，可见负色散峰值点的值与半峰全宽随着d2的变化趋势是相反的，要想实现宽带负色散必须以牺牲负色散值为代价.为了光纤实用性，希望负色散峰值点出现在1.55μm光通信窗口附近，因此选择小空气孔直径d2＝1.2μm，并在它保持不变的前提下，继续研究负色散特性随空气孔间距和大空气孔直径的变化规律.

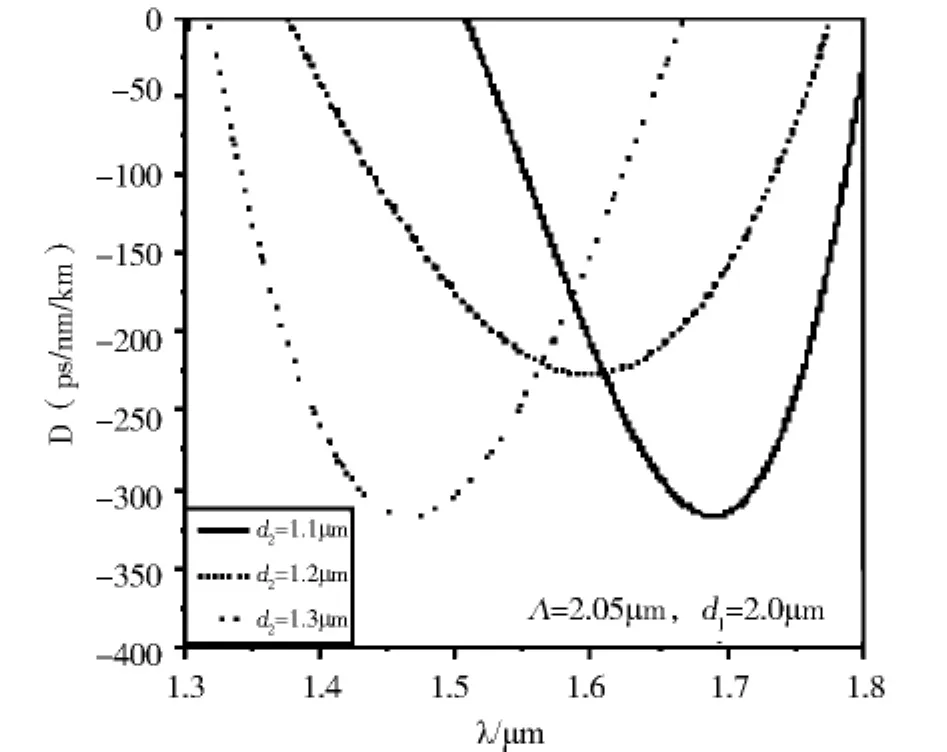
图5 当Λ＝2.05μm，d 1＝2.0μm时，d 2 对负色散的影响Fig.5 Effect of d 2 on negative dispersion properties（Λ＝2.05μm，d 1＝2.0μm）

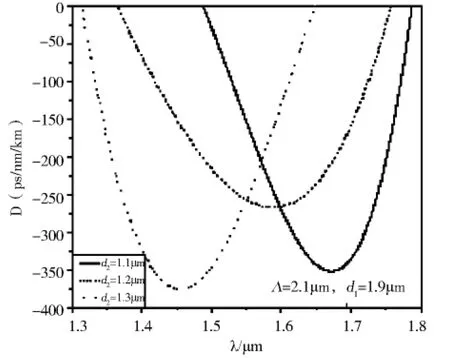
图6 当Λ＝2.1μm，d 1＝1.9μm时，d 2对负色散的影响Fig.6 Effect of d 2 on negative dispersion properties（Λ＝2.1μm，d 1＝1.9μm）

图7、8、9分别为负色散特性随空气孔间距Λ变化的关系曲线.选定小空气孔直径d2＝1.2μm保持不变，空气孔间距从2.0μm变化到2.1μm.从图中可以看出，在大小空气孔d1与d2保持不变的前提下，随着空气孔间距Λ的增大，负色散的峰值点都向右移动，且负色散的峰值在逐渐变小，色散曲线的形状有微小变化.同样，考虑到光纤实用性，先选定空气孔间距Λ＝2.05μm.

图7 当d 2＝1.2μm，d 1＝1.9μm时，Λ对负色散的影响Fig.7 Effect ofΛon negative dispersion properties（d 2＝1.2μm，d 1＝1.9μm）

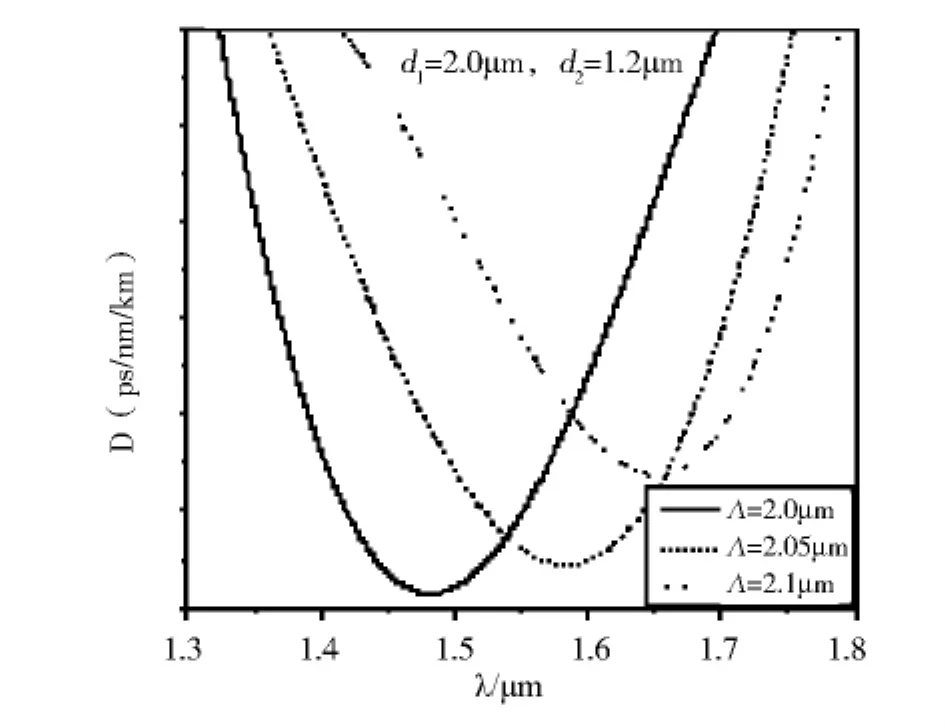
图8 当d 2＝1.2μm，d 1＝2.0μm时，Λ对负色散的影响Fig.8 Effect ofΛon negative dispersion properties（d 2＝1.2μm，d 1＝2.0μm）

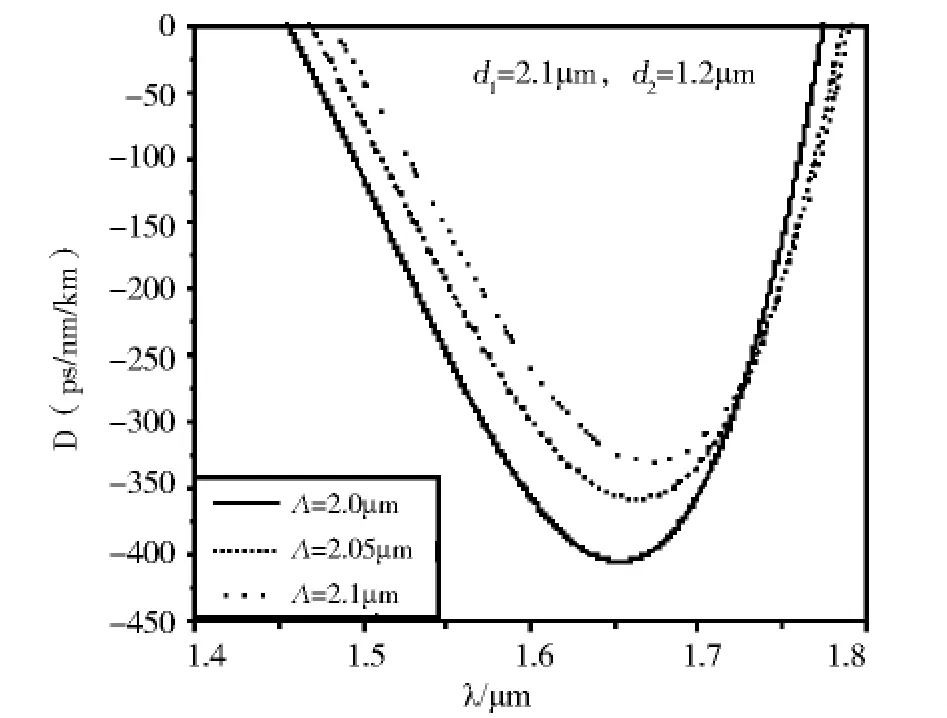
图9 当d 2＝1.2μm，d 1＝2.1μm时，Λ对负色散的影响Fig.9 Effect ofΛon negative dispersion properties（d 2＝1.2μm，d 1＝2.1μm）

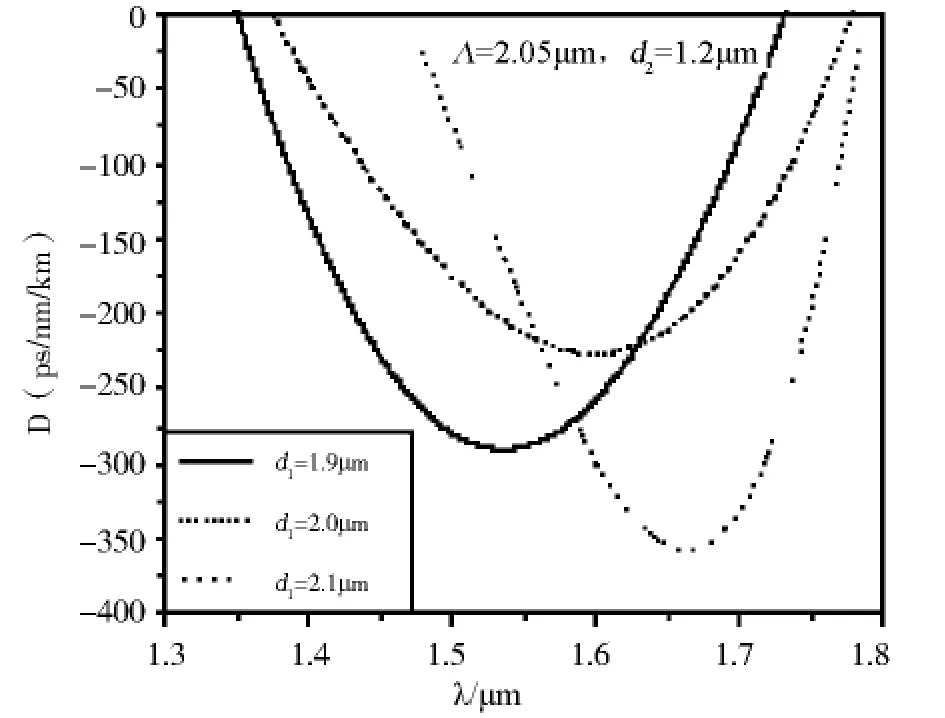
图10 大空气孔直径d 1对负色散特性的影响Fig.10 Effect of the large air－hole diameter d1 on negative dispersion properties

最后观察色散曲线随大空气孔直径d1的变化规律.图10为大空气孔直径d1与色散的关系图.图中空气孔间距Λ为2.05μm，小空气孔直径d2为1.2μm，大空气孔直径d1从1.9μm变化到2.1μm.从图中可以看出，随着大空气孔直径d1的增大，色散曲线的峰值点向右移动.

在我们所研究的结构参量范围内，当空气孔间距Λ＝2.05μm，大小空气孔直径分别为d1＝1.9μm，d2＝1.2μm时（即图10中实线所示的色散曲线），负色散曲线的峰值点最接近于1.55μm波长处，且半峰全宽也超过了200 nm，可见，我们设计的这种双芯复合正方形格点的光子晶体光纤同样具有宽带负色散特性.

从图4－图10中可以看出，这种光子晶体光纤的结构参量Λ（空气孔间距）、d1（小空气孔直径）和d2（小空气孔直径），对负色散特性的影响都比较显著.而我们分析的双芯复合六边形格点的光子晶体光纤［18］的负色散特性对结构参量的变化不太敏感，尤其是大空气孔直径的变化对负色散曲线只有微调作用，可见，按六边形格点排列的光子晶体光纤比按正方形格点排列的光子晶体光纤有更好的性能稳定性，从制作工艺上来讲，六边形格点比正方形格点也更加容易制作形成.

3 结论

本文设计了一种新的复合正方形格点双芯负色散光子晶体光纤，采用频域有限差分的方法研究了其负色散特性.研究表明，通过调节光纤的结构参量，可以得到不同程度的宽带负色散.例如，当空气孔间距Λ＝2.05μm，大小空气孔直径分别为d1＝1.9μm，d2＝1.2μm时，在1.55μm波长处，负色散的半峰全宽超过了200 nm.该光纤采用了复合格点结构，且采用的空气孔尺寸均大于1μm，这既给我们提供了较多的设计自由度，又减少了实际制作的困难.因此，我们设计的这种光子晶体光纤既有利于实际的制作，又可以用作波分复用光纤通信系统中的宽带色散补偿光纤.

［1］ Massimo Artiglia.Comparison of Dispersion Compensation Techniques for Lightwave Systems［C］／／OFC’98.San Jose：1998.Thv2：364－365.

［2］ Park Y K，Yeates P D，Delavaux J M P，etal.A field Demonstration of 20 Gbit／s Capacity Transmission over 360 km Installed Standard Fiber［J］.IEEEPhotonTechnolLett，1995，7（7）：816－818.

［3］ Watanabe S，Naito T，Chikama T.Compensation of Chromatic Dispersion in a Single Mode Fiber by Optical Phase Conjugation［J］.IEEEPhotonicsTechnolLett，1993，5（1）：92－95.

［4］ 黄俊，黄德修，李宏.通信系统中色散补偿光纤的研究［J］.光学与光电技术，2005，3（4）：11－12.

［5］ Antos A J，Smith D K.Design and Characterization of Dispersion Compensating Fiber Based on the LP01 Mode［J］.J LightwaveTechnol，1994，12：1739－1744.

［6］ Thyagarajan K，Varshney R K，Palai P，etal.A Novel Design of a Dispersion Compensating Fiber［J］.IEEEPhotonTechnolLett，1996，8：1510－1512.

［7］ Augugste J L，Blondy J M，Maury J，etal.Conception，Realization and Characterization of a Very High Negative Chromatic Dispersion Fiber［J］.Invitedpaper，OpticalFiberTechnol，2002，8：9－105.

［8］ Maury J，Auguste J L，Fevrier S，etal.Conception and Characterization of a Dual－concentric－core Erbium－doped Dispersion－compensating Fiber［J］.OptLett，2004，29：700－702.

［9］ Knight J C，Birks T A，Russell P St J，etal.All Silica Single－mode Optical Fiber with Photonic Crystal Cladding［J］.Opt Lett，1996，21（19）：1547－1549.

［10］ Cregan R F，etal.Single－mode Photonic Band Gap Guidance of Light in Air［J］.Science，1999，285：1537－1539.

［11］ Birks T A，Mogilevtsev D，Knight J C，etal.Dispersion Compensation Using Single－material Fibers［J］.IEEEPhoton TechnolLett，1999，11（6）：674－676.

［12］ Gerome F，Augugste J L，Blondy J M.Very High Negative Chromatic Dispersion in a Dual Concentric Core Photonic Crystal Fiber［C］／／OFC’04，February 22－27，2004，Los Angeles，California，WA2.

［13］ Ni Y，An L，Peng J，etal.Dual－core Photonic Crystal Fiber for Dispersion Compensation ［J］.IEEEPhotonTechnol Lett，2004，16（6）：1516－1518.

［14］ Gerome F，Augugste J L，Blondy J M.Design of Dispersion－compensating Fibers Based on a Dual－concentric－core Photonic Crystal Fiber［J］.OptLett，2004，29（23）：2725－2727.

［15］ Huttunen A，Torma P.Optimization of Dual－core and Microstructure Fiber Geometries for Dispersion Compensation and Large Mode Area［J］.OptExpress，2005，13（2）：627－635.

［16］ Yang Si－gang，Zhang Ye－jin，etal.Theoretical Study and Experimental Fabrication of High Negative Dispersion Photonic Crystal Fiber with Large Area Mode Field［J］.OptExpress，2006，14（7）：3015－3023.

［17］ Yang Si－gang，Zhang Ye－jin，etal.Broadband Dispersion－compensating Photonic Crystal Fiber［J］.OptLett，2006，31（19）：2830－2832.

［18］ 王红华，薛文瑞，张文梅.双芯复合格点光子晶体光纤的负色散特性［J］.光学学报，2008，28（1）：27－30.

［19］ 王红华，王淑娇.改进的正方形格点双芯光子晶体光纤的负色散特性分析［J］.量子光学学报，2009，15（4）：368－372.

［20］ Zhu Zhao－ming，Thomas G.Brown.Full－vectorial Finite－difference Analysis of Microstructured Optical Fibers［J］.OptExpress，2002，10（17）：853－864.

［21］ Guo Shang－ping，Wu Feng，Albin Sacharia.Loss and Dispersion Analysis of Microstructured Optical Fibers by Finitedifference Method ［J］.OptExpress，2004，12（15）：3341－3352.

［22］ Yu Chin－ping，Chang Hung－chun.Yee－mesh－based Finite Difference Eigenmode Solver with PML Absorbing Boundary Conditions for Optical Waveguides and Photonic Crystal Fibers［J］.OptExpress，2004，12（25）：6165－6177.

［23］ 武延荣，郭丽霞，薛文瑞，等.单偏振光子晶体光纤［J］.光学学报，2007，27（4）：593－597.

［24］ 郭丽霞，武延荣，薛文瑞，等.复合六边形空气孔格点光子晶体光纤的色散特性分析［J］.光学学报，2007，27（5）：935－939.

［25］ 何忠蛟.矩形孔光子晶体光纤 ［J］.光子学报，2011，40（4）：583－586.

［26］ Zhang Shan－shan，Zhang Wei－gang，Geng Peng－cheng，etal.Design of Single－polarization Wavelength Splitter Based on Photonic Crystal Fiber［J］.AppliedOptics，2011，50（36）：6576－6582.

［27］ Agrawal G P.Nonlinear Fiber Optics［M］.（Third Edition），San Diego：Academic Press，2001.

Negative Dispersion Properties of Photonic Crystal Fiber with Dual－Core and Composite Square Lattice

WANG Hong－hua，SUN Yu－mei
（CollegeofElectronicEngineering，YantaiNanshanUniversity，Longkou265713，China）

A dual－core and negative dispersion photonic crystal fiber（PCF）with composite square lattice is introduced，in which the cladding is composed of two different air holes based on pure silica and the inner core is formed with high effective index dopped material.In order to realize negative dispersion，the third ring of air holes in the cladding is omitted.Using the finite difference frequency domain algorithm，the negative dispersion properties are analyzed.The results show that the broadband negative dispersion with different levels can be achieved by optimizing air－hole pitch and two air－hole diameters.The broadband negative dispersion with full width at half maximum exceeding 200 nm is realized at 1.55μm wavelength when the radius of the inner core，the center to center distance of holes，the diameter of the larger hole and the diameter of the smaller hole is 0.95μm，2.05μm，1.9μm，1.2μm respectively.So this fiber can be used for broadband dispersion compensation in wavelength－division multiplexing optical fiber communication systems.

fiber optics；photonic crystal fiber（PCF）；negative dispersion；finite difference frequency domain method（FDFD）

TN913.7

A

0253－2395（2012）04－0669－06＊

2010－09－27；

2012－12－

烟台南山学院特色专业经费项目（TS1004）

王红华（1981－），女，山东烟台人，烟台南山学院教师，研究方向为光纤光学和光子晶体光纤.＊通信联系人：E－mail：whh＿613＠126.com