＊ 非线性色散耗散波动方程的最低阶非协调有限元分析

樊明智，王芬玲，石东洋

（1.许昌学院 数学与统计学院，河南 许昌 461000；2.郑州大学 数学系，河南 郑州 450052）

＊非线性色散耗散波动方程的最低阶非协调有限元分析

樊明智1，王芬玲1，石东洋2

（1.许昌学院 数学与统计学院，河南 许昌 461000；2.郑州大学 数学系，河南 郑州 450052）

在半离散和全离散格式下讨论了一类非线性色散耗散波动方程的Crouzeix－Raviart型非协调线性三角形有限元逼近，得到了H1模意义下两种离散格式的最优误差估计.

非线性色散耗散波动方程；非协调有限元；最优误差估计；半离散和全离散格式

考虑下面非线性色散耗散波动方程

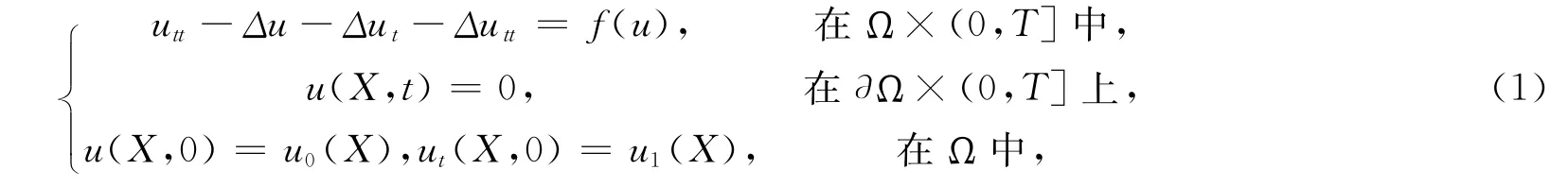
其中Ω⊂R2有界凸区域，∂Ω为 Ω的边界，X＝（x，y），u0（X），u1（X）是光滑函数，f（u）满足Lipschitz条件，

非线性色散耗散波动方程是从非线性弹性杆中纵向形变传播及弱非线性作用下空间变换离子声波传播问题中提出的，是一类具有强烈物理背景的非线性发展方程.关于该类方程已有一些研究［1－7］，其中文［1］讨论了其整体强解的存在性和唯一性，并在一定条件，研究了解的渐近性质和blow up现象；文［2］使用乘子法，证明了整体强解在关于非线性项简单而宽泛的假设下，随时间趋于无穷而衰减到零；文［3－4］采用位势井方法探讨了此类方程的柯西问题和初边值问题；文［5－6］研究了该类多维方程的柯西问题整体解的存在性；文［7］对于问题（1）有限元的数值解法进行了研究，它给出了半离散和全离散协调有限元格式，并证明了这两种格式解的存在性和唯一性，得到了在L2和H1模意义下有限元解与原方程精确解间的误差估计.但据我们所知，针对问题（1）的非协调有限元方法少见报道.

在非协调元中，Crouzeix－Raviart型线性非协调三角形元是自由度最小的一个，它已广泛地应用于许多问题［8－12］.例如，文［8］和［9］在正则网格下，应用该元分别对单侧问题和位移障碍变分不等式进行了有限元分析；文［10］研究了Signorini变分不等式问题的非协调元逼近，得到了相应的最优误差估计；文［11］将该元应用到非定常Navier－Stokes方程，给出了其质量集中有限元逼近格式，在各向异性网格下导出了速度的L2和H1模及压力的L2模的误差估计；文［12］讨论了粘弹性方程的非协调变网格有限元方法，得到了最优误差估计.本文的目的是将低阶Crouzeix－Raviart型非协调三角形有限元应用于问题（1），在与文［7］不同的半离散和全离散有限元逼近格式下，导出了H1模意义下两种离散格式的最优误差估计，拓展了非协调元的应用范围.

1 半离散格式及误差估计

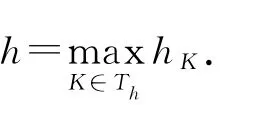
Crouzeix－Raviart型线性非协调三角形有限元空间V h定义为［8］

选择适当小的ε，τ，使得1－ε－Cτ＞0，根据离散的Gronwall引理得（17），再结合三角不等式导出（18），从而定理得证.

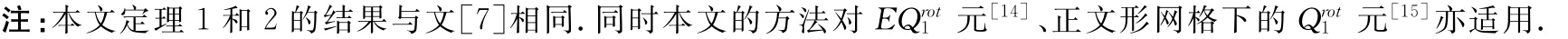
［1］ 尚亚东.方程utt－Δu－Δut－Δutt＝f（u）的初边值问题［J］.应用数学学报，2000，23（3）：385－392.

［2］ 徐润章，赵希人，沈继红.具色散耗散项的四阶波动方程解的渐近性质［J］.应用数学与力学，2008，29（2）：235－238.

［3］ Liu Y C，Xu R Z.Potential Well Method for Cauchy Problem of Generalized Double Dispersion Equations［J］.JMathA－nalAppl，2008，338（2）：1169－1187.

［4］ Liu Y C，Xu R Z.Potential Well Method for Initial Boundary Value Problem of the Generalized Double Dispersion Equations［J］.CommunPureApplAnal，2008，7（1）：63－81.

［5］ Xu R Z，Liu Y C.Global Existence and Nonexistence of Solution for Cauchy Problem of Multidimensional Double Dispersion Equations［J］.JMathAnalAppl，2009，359（2）：739－751.

［6］ Xu R Z，Liu Y C，Yu T.Global Existence of Solution for Cauchy Problems of Multidimensional Generalized Double Dispersion Equations［J］.NonlinearAnalysis，2009，71（10）：4977－4983.

［7］ 孙同军.一类高维非线性色散耗散波动方程的有限元分析［J］.山东大学学报：理学版，2003，33（6）：712－716.

［8］ Wang L H.Nonconforming Finite Element Approximation of Unilateral Problem［J］.JComputMath，1999，17（1）：15－24.

［9］ Wang L H.On the Error Estimate of Nonconforming Finite Element Approximation to the Obstacle Problem［J］.JComputMath，2003，21（4）：481－490.

［10］ 石东洋，毛士鹏，陈绍春.问题变分不等式的一类各向异性Crouzeix－Raviart型有限元逼近［J］.计算数学，2005，27（1）：45－54.

［11］ 石东洋，王慧敏.非定常Navier－Stokes方程的质量集中各向异性非协调有限元逼近［J］.数学物理学报，2010，30A（4）：1018－1029，

［12］ 石东洋，关宏波.粘弹性方程的非协调变网格有限元方法［J］.高校应用数学学报，2008，23（4）：452－458.

［13］ 石东洋，张熠然.非定常Stokes问题的矩形Crouzeix－Raviart型各向异性非协调元变网格方法［J］.数学物理学报，2006，26A（5）：659－670.

［14］ Lin Q，Lin J F.Finte Element Methods：Accuracy and Improvement［M］.Beijing：Science Press，2006.

［15］ Rannacher R，Turek S.Simple Nonconforming Quadrilateral Stokes Element［J］.NumerMethPDEs，1992，8（2）：97－111.

A Lowest Order Nonconforming Finite Element Analysis for Nonlinear Dispersion－Dissipative Wave Equations

FAN Ming－zhi1，WANG Fen－ling1，SHI Dong－yang2
（1.SchoolofMathematicsandStatistics，XuchangUniversity，Xuchang461000，China；
2.DepartmentofMathematics，ZhengzhouUniversity，Zhengzhou450052，China）

A Crouzeix－Raviart type nonconforming linear triangular finite element approximation is discussed for a class nonlinear dispersion－dissipative wave equations under semi－discrete and fully－discrete schemes，the optimal order error estimates in brokenH1norm were derived for two discrete schemes.

nonlinear dispersion－dissipative wave equations；nonconforming finite element；the optimal order error estimate；semi－discrete and fully－discrete schemes

O242.21

A

0253－2395（2012）04－0603－05＊

2012－02－11；

2012－04－10

国家自然科学基金（10971203）；高等学校博士学科点专项科研基金（20094101110006）；河南省教育厅自然科学基金（12A110021）

樊明智（1969－），男，河南鄢陵人，硕士，副教授，主要从事有限元方法及应用研究.