*一类非线性Klein-Gordon方程非协调有限元超收敛分析
2012-01-11任金城
任金城
(商丘师范学院 数学系,河南 商丘 476000)
*一类非线性Klein-Gordon方程非协调有限元超收敛分析
任金城
(商丘师范学院 数学系,河南 商丘 476000)
对一类非线性Klein-Gordon方程利用五节点非协调有限元进行了高精度研究.首先,讨论在半离散格式下解的收敛性;其次,利用单元自身的特殊性质和一些新的分析技巧得到了超逼近性质;最后,通过构造一个插值后处理算子导出了整体超收敛结果.
Klein-Gordon方程;非协调有限元;高精度分析;超收敛
考虑下面一类非线性Klein-Gordon方程
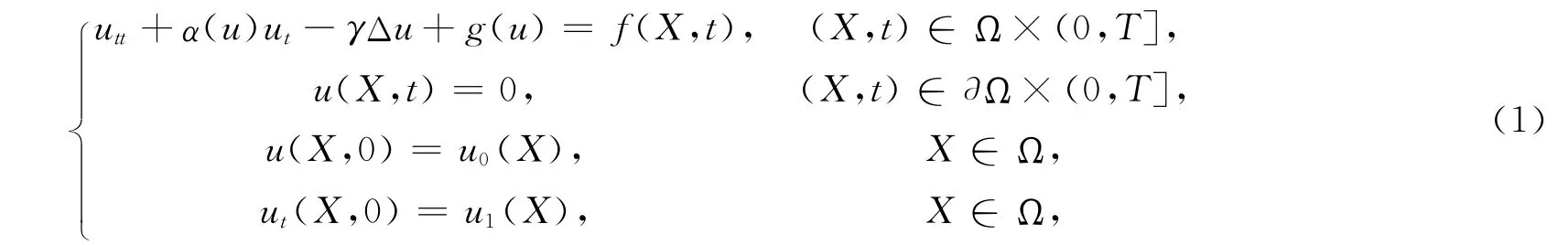
其中X=(x,y),Ω⊂R2为有界区域,∂Ω为其光滑边界,γ为正常数,α(u),g(u)对变量u满足Lipschitz连续条件,以及存在正常数α0,α1,使得α0≤α(u)≤α1,并且具有二阶光滑导数.
Klein-Gordon方程是相对论量子力学和量子场论中用于描述自旋为零的粒子的最基本方程式,具有深刻的实际背景和物理意义,受到了一些物理学家和数学家的高度关注[1-6].
文[1]研究了无限齐次波管在小参数情况下非线性Klein-Gordon方程整体解的存在性.文[2]研究了二维的非线性Klein-Gordon方程在参数足够小的情况下存在唯一的整体解.文[3]提出了一个交叉约束变分的方法来研究非线性Klein-Gordon方程,利用交叉约束变分问题,建立所谓的交叉不变流形的演变流,最后给出了初始值与整体解的存在关系,这些研究均偏重于偏微分方程解的理论的分析.文[4]中对无界区域一维的非线性Klein-Gordon方程建立一个显式差分格式,由能量分析法得到了该格式稳定性和收敛性的结果;文[5]和[6]研究了一维的非线性Klein-Gordon方程的数值解.近来由于非协调元的一些独特优势吸引了大批的科学家和工程人员,首先,它比协调元更加容易满足离散的inf-sup条件;另一方面,从区域分解的观点来看,由于非协调元的自由度大多都定义在单元的边上,这样每个自由度至多为两个单元共用,在信息交换方面提供了非常便利的条件[7],而对于二维情形非协调有限元数值方法研究的文献还不多见.
本文将文[8-9]中的单元应用于二维的非线性Klein-Gordon方程,给出方程在半离散格式下解的收敛性;同时,利用单元的正交性、相容误差比插值误差高一阶的特点得到了相应的超逼近性质;最后,通过构造一个合适的插值后处理算子导出了整体超收敛结果.
1 收敛性分析
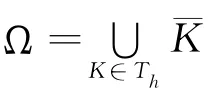


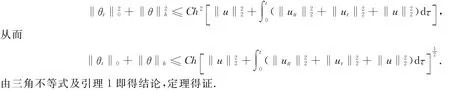
2 超逼近及超收敛分析

3 结论及评注
本文正是利用单元的正交性即((▽(u-Ihu),▽v)=0,∀v∈V h)以及相容误差比插值误差高一阶的特点和对边界项利用导数转移技巧得到了超逼近的性质,从而得到本文超收敛的结果.最后,通过构造一个合适的插值后处理算子导出了整体超收敛结果,并且得到了关于u离散能量模的最优误差估计.
注2:从文中可以看出,证明过程并不需要网格剖分满足传统有限元的正则性和拟一致假设,说明这一假设对有限元分析来说并不是必要的条件.
[1] Fang D Y,Tong C Q,Zhong S J.Global Existence for Nonlinear Klein-Gordon Equations in Infinite Homogeneous Waveguides in two Dimensions[J].JMathAnalAppl,2007,331(1):21-37.
[2] Nakao H,Pavel I N.Wave Operators to a Quadratic Nonlinear Klein-Gordon Equation in two Space Dimensions[J].NonlinearAnalTMA,2009,71(9):3826-3833.
[3] Gan Z H,Guo B L,Zhang J.Sharp Threshold of Global Existence for the Klein-Gordon Equations with Critical Nonlinearity[J].ActaMathApplSinica,2009,5(2):273-282.
[4] Han H D,Zhang Z W.An Analysis of the Finite-difference Method for One-dimensional Klein-Gordon Equation on Unbounded Domain[J].ApplNumerMath,2009,59(7):1568-1583.
[5] Khalifa M E,Elgamali M.A Numerical Solution to Klein-Gordon Equation with Dirichlet Boundary Condition [J].Appl MathComput,2005,160(2):451-475.
[6] Wang Q F,Cheng D Z.Numerical Solution of Damped Nonlinear Klein-Gordon Equations Using Variational Method and Finite Element Approach[J].ApplMathComput,2005,162(1):381-401.
[7] Dougla Jr J,Santos J E,Sheen D,etal.Nonconforming Galerkin Methods Based on Quadrilateral Elements for Second Order Elliptic Problems[J].RAIROModelMath.AnalNumer,1999,33(4):747-770.
[8] Shi D Y,Mao S P,Chen S C.An Anisotropic Nonconforming Finite Element with Some Superconvergence Results[J].J ComputMath,2005,23(3):261-274.
[9] Lin Q,Tobiska L,Zhou A H.Superconvergence and Extrapolation of Nonconforming Low Order Elements Applied to the Poisson Equation[J].IMAJNumerAnal,2005,25(1):160-181.
[10] Shi D Y,Wang H H,Du Y P.An Anisotropic Nonconforming Finite Element Method for Approximating a Class of Nonlinear Sobolev Equations[J].JCompMath,2009,27(2-3):299-314.
[11] Ciarlet P G.The Finite Element Method for Elliptic Problems[M].Amstedam,New York:North-Holland,1978.
[12] Shi D Y,Ren J C.Nonconforming Mixed Finite Element Approximation to the Stationary Navier-Stokes Equations on Anisotropic Meshes[J].NonlinearAnalTMA,2009,71(9):3842-3852.
[13] Shi D Y,Peng Y C,Chen S C.Superconvergence of a Nonconforming Finite Element Approximation to Viscoelasticity Type Equations on Anisotropic Meshes[J].NumerMathJChineseUniversity,2006,15(4):375-384.
Superconvergence Analysis on Nonconforming Finite Element for a Classe Nonlinear Klein-Gordon Equations
REN Jin-cheng
(DepartmentofMathematics,ShangqiuNormalUniversity,Shangqiu476000,China)
The higher accuracy analysis of a five-node nonconforming finite element to the nonlinear Klein-Gordon equations is discussed.Firstly,the convergence of solution to this equation is obtained under semidiscretization.Secondly,the result of superclose are derived through the element’s special property and some novel approaches.Finally,based on the interpolated postprocessing technique,the global superconvergence is derived.
nonlinear Klein-Gordon equations;nonconforming finite element;higher accuracy analysis;superconvergence
O242.21
A
0253-2395(2012)04-0608-05*
2011-03-18;
2011-12-21
江苏省高校研究生科研创新项目(CXZZ11_0134);商丘师范学院青年基金(2010QN013)
任金城(1982-),男,河南南阳人,博士,主要从事有限元方法及其应用的研究.E-mail:renjincheng2001@126.com
book=612,ebook=320
