基于二维灰度图像的规则形体三维重建

钱苏斌

(盐城师范学院信息科学与技术学院,江苏盐城 224002)

0 引 言

目前,由形体的二维灰度图像构建其三维形状已经成为计算机视觉领域的一个研究热点.现实世界中广泛存在的形体主要分为规则形体与非规则形体两类.前者主要是一些能够用简单数学形式表达的形体,这类形体不仅包括平面、长方体、立方体,还包括一些二次曲面体,如柱体、球体、椎体等;后者则表现为一些较为复杂的自由曲面体.在计算机视觉领域,研究人员已经提出了一些规则形体重建的方法[1-3],但这些方法得到的只是重建对象的相似模型,并没有能够实现物体的精确测量与重建.本研究拟对基于规则形体的三维重建方法进行探讨,并提出一种基于单幅灰度图像,利用规则形体的“对称特性”进行三维重建的方法,这种方法充分利用规则形体的特殊几何特性,高效、快捷地实现了形体的三维重建.

图1 规则形体对称性

1 对称性规则形体的三维重建方法

1.1 规则形体的对称性

客观世界中的规则形体,无论是平面、长方体或者旋转体都具备一个共同的特性,即几何对称性.例如,图1(a)所示的长方体中,存在一个空间平面C1,使得长方体本身相对于空间平面 C1对称,这个空间平面即称之为对称面.如图1(b)所示的圆柱体中,必定存在一条空间直线L1,使得圆柱体本身相对于这条空间直线L1对称,这条空间直线即称之为对称轴.

根据上述几何对称特性,本研究提出一种基于规则形体的对称轴或对称面进行形体三维重建的方法:首先,对单幅图象中提取出来的形体进行特征分析,提取出相关特征点构造形体的对称轴或对称面;其次,利用对称轴或对称面,结合上述特征信息完成形体的三维重建.

1.2 对称面空间推移法

1.2.1 特征点提取.

如图2(a)所示为1幅由数码照相机拍摄得到图片,对其进行非线性平滑滤波处理及必要的颜色转换后获取的256色灰度图像,其中目标区域为长方体.对该灰度图进行阈值分割[5]操作,结果如图2 (b)所示.根据重建要求,提取出该长方体的整体轮廓线,观察该位图,其中目标区域只有一个,利用单目标区域轮廓跟踪方法[6],得到如图2(c)所示的整体轮廓线.

1.2.2 确定对称面.

在图像处理的过程中,形体所占的空间区域具备多种局部特征,其中形体本身的边缘线间相交的交点便是其具备的局部特征之一,通常将该交点称之为角点.本研究利用一种自适应的Harris角点检测算法[7]对长方体整体轮廓线进行角点检测,如图3所示的角点 P1、P2、P3、P4、P5、P6,其中角点以“+”标记.

图2 长方体特征分析

图3 特征点提取

图4 确定对称面

利用角点检测算法检测出长方体表面的6个角点,由于数码相机在拍摄过程中的角度问题,所获取的图像与实际物体在形状上存在较小的视觉偏差.为了确保重建的精确性,选取空间上距离视角最近的作为基边,P7为基边的中点(见图4),过该点作的中垂线,并且与P3P4相交于点 P8,与相交于 P9.根据3点确定一个平面的原理,由 P7、P8、P9 3点确定一个平面,同时,根据长方体几何特性,角点 P1、P2、P5、P6 4点确定一个平面 F,即长方体的前表面,在平面 F对立面的底边上必定存在一点P10,该点在 P7、P8、P93点共同确定的平面内,这里将由上述4点共同确定的平面标记为平面S,即平面S即为该长方体的对称面(见图4).

1.2.3 形体表面三维信息获取.

长方体由若干平行于对称面的小平面(以下称子平面)共同构成,在对称面确定之后,可以通过将对称面进行空间推移的方法,依次形成各子平面,从而最终重建出整个形体的三维形状.

图5 空间推移法

设置一个二维的点结构体数组cuboidpoint[] [],用于存放所有子平面上的点,每个点对应存放在点结构体数组cuboidpoint[count][i],其中count对应于构成形体的第count个子平面,i对应于第count个子平面上的第 i个像素点,将 i的下限设置为0,上限设置为 d,并通过下列for循环可以直观的得到形体上对称面右侧的任意一个子平面上像素点的三维坐标信息,同理,可通过坐标分析,得到对称面左侧的任意一个子平面上像素点的三维坐标信息.

由此可见,根据上述方法,可以快速地获取一些简单的规则形体(如长方体、立方体等)的三维表面信息,从而完成其三维形状的构造.

1.3 对称轴空间推移法

现实中,旋转体也是比较多见的规则形体之一,其中由圆弧面结合其他曲面构成的复杂旋转体比较常见,如陶瓷、玻璃工艺制品.本研究在分析对称轴空间推移法时,所采用的研究对象是表面构成中含有圆弧面成分的旋转体,即母线由弧线与直线或者其他一部分二次曲线拼接而成的旋转体对象.

1.3.1 特征点提取.

图6(a)所示为一只花瓶,图6(b)、6(c)是对该花瓶分别进行阈值分割及轮廓跟踪后的效果.为了方便后续的特征信息提取,同样采用角点检测方法得到如图6(d)所示的角点信息.

图6 旋转体特征分析

1.3.2 确定对称轴.

(1)有效轮廓线提取及分段.观察图6(c)所示的旋转体的闭合轮廓线,可得知旋转曲面的构成仅需其中的左、右两条轮廓线.这里结合角点坐标信息,采用域截取方法截去上下两条多余的轮廓线,从而提取出如图7所示的两条有效轮廓线L1、L2.利用多目标轮廓跟踪算法,对两条有效轮廓线分别进行轮廓跟踪(双轮廓跟踪方法)并标识特征点(见图8).将L1分段曲线分别标记为 C1、C2,C1、C2均为圆弧曲线段.

(2)确定旋转体对称轴.由于瓶体的母线中含有的 C1、C2曲线段均为圆弧,所以根据瓶体表面的几何对称性只要确定其中之一的对称轴,即可将该对称轴作为整个瓶体表面的对称轴.本研究利用坐标变换方法[8],通过 C2曲线段去获取了整个瓶体表面的对称轴(见图9),I1、I3分别为弧段 C2的起点和终点,L即为旋转体的对称轴,I4、I5、I6即为 I1、I2、I3关于对称轴L的对称点.

图7 有效轮廓线提取

图8 有效轮廓线分段

为了处理的方便,将图9中的对称轴L旋转一定的角度,使得L平行于Y轴,旋转变换后得到如图10的变换结果,其中L′为变换后的对称轴,T1、T2、T3、T4、T5、T6分别为 I1、I2、I3、I4、I5、I6经过变换后的对应坐标.

图9 确定对称轴

图10 坐标变换分析

1.3.3 旋转体表面三维信息获取.

瓶体表面是由L1围绕对称轴L′旋转一周所形成的旋转曲面,即等价于构成L1的若干个像素点围绕对称轴L′旋转一周所形成的一系列纬圆的集合,如图10中 C即为 T1点围绕L′旋转所形成的纬圆.

设置一个二维的点结构体数组vasepoint[][],用于存放所有纬圆上的点,每个点对应存放在点结构体数组vasepoint[count][i],其中,count对应于其中一条有效轮廓线上第count个像素点,i对应于由该点围绕对称轴旋转时得到的第 i个轨迹点.设,0≤i≤360,且 i为整数.这里将其转化为弧度,并且记vasepoint[count][i]的3个分量为(nx,xy,xz),所以得到旋转曲面上若干个像素点坐标的显式表达为:

根据上述方法,可以快速地获取一些表面构成中含有圆弧面成分的旋转体表面的三维信息,从而完成旋转体三维形状的构造.

2 实验结果

在实验中,本研究以OpenG L和VC++6.0为开发工具,根据本文所提出的规则形体三维重建方法,实现一个基于形体对称性的三维重建系统,并利用该系统实现了上述两个比较典型的规则形体的三维重建效果,结果如图11(a)、11(b)所示.

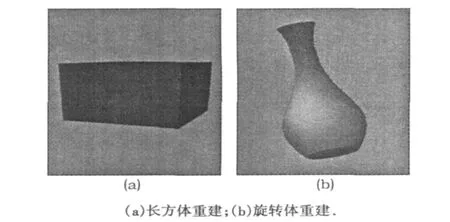
图11 规则形体三维重建效果

实验结果表明,本文所提出的基于对称轴或对称面推移方法能够快速、高效地从物体的二维灰度图像构建出其三维形状.

3 结 论

本文所提出的基于二维灰度图像的规则形体三维重建方法,其根据规则形体自身所具备的特殊几何对称特性,利用特征信息构建对称轴或者对称面,再通过对称轴或对称面推移法方便快捷的实现规则形体表面的三维重建.该方法不仅有效避免了一般重建方法需要用较多的几何参数去精确表示曲面形态的缺陷,而且在一定程度上提高了重建的精度.

[1]王越.空间曲面三维重建关键技术的研究[D].哈尔滨:哈尔滨工业大学,2004.

[2]Wong K Y K,Mendonca P R S,Cipolla R.Reconstruction of Surfaces of Revolution from Single Uncalibrated Views[C]//British Machine Visition Conference,British,2002.Cardiff,U.K: IEEE Press,2002:93-102.

[3]Utcke S,Zisserman A.Projective Recontruction of Surfaces of Revolution[J].Lecture Notes in Computer Science,2003,2781 (1):265-272.

[4]郑顺义,徐刚,张祖勋,等.旋转体三维重建方法研究[J].武汉大学学报,2006,31(12):1047-1050.

[5]钱苏斌.基于四邻域检索的自适应阈值分割方法[J].成都大学学报(自科版),2011,30(3):239-241.

[6]石爽,曲仕茹,何力.一种新的边界跟踪算法[J].工程图学学报,2011,32(3):52-56.

[7]侯建辉,林意.自适应的Harris棋盘格角点检测算法[J].计算机工程与设计,2009,30(20):4741-4743.

[8]钱苏斌,林意.基于轮廓线的旋转曲面三维重建[J].计算机工程与设计,2009,30(16):3875-3878.