数字散斑相关方法在实验力学中的适用性

刘亚双

(苏州建设交通高等职业技术学校,江苏苏州 215104)

0 引 言

数字散斑相关方法[1]是一种发展迅速的光力学测量技术,它是固体实验力学领域材料表面变形场测量的一种非接触式方法,与其他光力学测量技术相比具有全场测量、非接触、光路相对简单、测量视场可以调节、不需要光学干涉条纹处理、可适用的测试对象范围广以及对测量环境无特别要求等突出的优点.经过20多年的发展,目前该技术的应用已经从最初的实验应力分析扩展到很多相关领域,如固体力学、流体力学、生物力学、复杂材料本构关系的确定、微尺度力学领域、电子封装以及工程检测与无损检测等[2-4].但是在这些领域中的应用主要是针对微小位移和变形的研究,对于像桥梁工程中的大位移及变形这样的研究工作涉及较少.

1 数字散斑相关方法的基本原理

通常说的数字散斑相关方法一般是指二维的数字散斑相关方法,该方法是根据物体表面随机分布的散斑场在变形前后的统计相关性来确定物体的变形,其基本思想是:分别采集物体变形前后的两幅数字散斑图,如果将变形前的图像中的一小块图像定义为样本子区,变形后的图像中与样本子区相对应的那一小块图像定义为目标子区,则只要找出目标子区和样本子区之间的一一对应关系,就可以实现变形量的提取.样本子区与目标子区的位置差别包含了位移分量,形状差别包含了应变分量,这样就把变形测量问题转化为一个数字化相关计算过程[2].在相关计算中,首先需要寻找一组合适的变量来表征变形前后图像中子区的位移和变形,然后建立一个衡量图像相似的数学标准,以此判断在目标图像中的一个子区是否与样本图像中给定的子区对应,最后选择一种高效的搜索算法,如牛顿-拉斐森迭代法及拟牛顿迭代法[3-4],求解获得分析对象的位移和应变数值.

2 数字散斑相关方法的适用性验证

2.1 刚体平动位移实验

刚体平动位移实验通过在一刚体上喷散斑来进行,刚体的高度和宽度分别为79 mm、63 mm,将其固定在精密微调架上.旋转微调架的转圈,使刚体的横向位移为0 mm,纵向位移分别为0.3 mm、0.4 mm.编制散斑搜索程序,在搜索时选取子区大小为41× 41.这里取刚体横向象素坐标为x=450,y=100到x =550,y=100表示的一条直线上的搜索计算结果作为分析对象.将微调架的标尺刻度读数与用数字散斑相关搜索方法搜索的物体位移进行比较.图1所示为竖向位移值是0.3 mm时的像素搜索值,表1为在不同测距下的分析结果.

图1 刚体竖向位移计算值

表1 刚体位移对比实验数据及计算结果

由表1数据和图1可见,用本研究自编的程序搜索得到的位移值基本在一条水平线上,误差仅为0.01个像素,即5.6×10-4mm,且随着位移值的增大,读数值与搜索值之间的误差会减小.

2.2 橡胶拉伸实验

拉伸实验试件为橡胶材料制成的矩形模型,其尺寸为,长19 cm、宽2.6 cm.本实验利用万能实验机对模型进行拉伸,实验机与电脑相连,通过电脑严格并准确的控制万能实验机的位移,实验装置如图2所示.

图2 拉伸实验装置图

这里取x=450,y=100到x=550,y=100表示的一条直线上的计算结果作为分析对象.本实验象素标定值为,0.0139 mm/pixel.图3所示为橡胶拉伸0.4 mm时的像素搜索值,表2为橡胶拉伸对比实验数据.

图3 橡胶拉伸实验计算值

由由图3、表2可以看出,用本研究自编的数字散斑搜索程序计算得出,在同一条水平线位移值基本上都相等,误差不超过10%,仅为0.01个像素,即1.4×10-4mm.

2.3 简支梁三点弯实验

简支梁三点弯实验模型为环氧树脂材料制成的简支梁,截面为矩形,梁高18.2 mm.将其放置在万能实验机上,实验装置与拉伸实验相同.采用控制梁中点位移的方式加载,实验机与计算机相连,通过计算机严格准确控制梁中点位移为0.5 mm(见图4).

表2 橡胶拉伸对比实验数据及计算结果

理论上分析,三点弯梁在中点荷载作用下,弯矩图为抛物线形,梁的各点变形分布规律也是抛物线形.

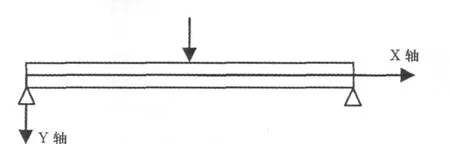
图4 简支梁简图

实验结果如图5、图6所示.图5为在梁中点左侧一段上Y=100的纵断面上从X=450到X=550的每隔10个像素点的变形图;图6为在梁中点右侧一段上Y=100的纵断面上从X=450到X=550的每隔10个像素点的变形图.

图5 中点左侧Y轴向变形图

图6 中点右侧Y轴向变形图

由图5、6可见,利用本研究自编的搜索程序计算得到的三点弯梁中点附近挠度曲线类似于抛物线形,与理论挠度线形式相同.

3 结 论

本研究通过刚体平动实验、橡胶拉伸实验以及环氧树脂三点弯梁实验,验证了应用数字散斑相关方法测量物体的大变形和位移具有一定的适用性.

[1]芮嘉白,金观昌,徐秉业.一种新的数字散斑相关方法及其应用[J].力学学报,1994,26(5):599-607.

[2]王怀文,亢一澜,谢和平.数字散斑相关方法与应用研究进展[J].力学进展,2005,35(2):195-203.

[3]简龙恢,林壁森,刘宁,等.基于小波变换的新型数字散斑相关方法[J].光学技术,2003,29(2):216-218.

[4]高建新,周辛庚.变形测量中的数字散斑相关搜索法[J].实验力学,1991,6(4):121-127.

[5]金波,李鸿琦,刘祥君.数字图像处理技术在桥梁检测中的应用[J].机床与液压,2004,32(9):110-112.