格上基于身份的代理环签名方案
2012-01-10张利利马艳琴
张利利,马艳琴
(黄河科技学院信息工程学院,河南郑州 450063)
0 引 言
1984年,Shamir[1]提出基于身份的公钥密码体制,其简化了基于证书的公钥体制负担最重的密钥管理过程.1996年,Mambo等[2]提出代理签名,利用代理签名,原始签名人可以将他(她)的签名权委托给代理签名者,对任何消息代理人都可以进行签名,任何人只要知道原始签名人的公钥就可以对代理签名进行验证.2001年,Rivest等[3]提出环签名,其实际上是一种简化的群签名,它仅包括环成员而没有管理者,不需要群建立过程,也无法撤销真实签名者的匿名性,签名验证者可以确定签名来自某个环成员,但无法确定签名者的具体身份,因而可以有效地保护实际签名者的隐私权.根据对代理人保持匿名的应用,2003年,Zhang[4]提出了代理环签名的方案,并给出第一个基于身份的代理环签名方案:当授权人将签名权利授予很多代理人时,这些代理人组成了一个代理人集合,每个代理人都可以代替授权人执行签名操作,并且可不被任何人(包括授权人)揭开他的身份.2006年,杨少春[5]提出了一种更加高效的代理环签名方案,计算量得到很大的改善.但是,这些代理环签名方案大部分都是基于大整数分解和离散对数问题的,在量子计算机得到应用的前提下,大整数分解问题和离散对数问题都可以利用多项式时间算法解决.因此,设计能抵抗量子攻击的代理环签名方案成为该领域需解决的问题.近年来,基于格构造的新型密码系统因具有运算简单(通常只需要线性运算)、能抵抗量子攻击和存在最坏情况下的随机实例等特点,成为公钥密码领域的研究热点,并取得了一系列的研究成果[6-9].本研究基于格上的SIS和 ISIS问题的困难性,利用原像抽样函数[6]和格基代理算法[9]构造了一个格上基于身份的无可信中心的代理环签名方案.
1 基础知识
1.1 格
设 b1,b2,…,bn是Rm上一组的量,令B=[b1, b2,…,bn]⊆ Rm×n,则由 B生成的n为格定义为,

Λ(B)的正交格定义为,

设ω是一个向量,ω的lp-范数定义为,

当p=2时,称作欧几里得范数,简记为‖ω‖.
1.2 格上的困难问题
(1)SVP问题(最短向量问题).设A是格的一组基,SVP问题就是在格上寻找一个非零向量u,满足任意格上的向量v,有 ‖u‖≤‖v‖成立.其中 ‖·‖为给定的范数.
(2)SIS问题(小整数解问题).给定整数 q,实数β,矩阵A∈Zn×mq,寻找一个非零向量 e,满足Ae= 0modq,且 ‖e‖≤β.
(3)ISIS问题(非齐次小整数解问题).给定整数q,实数β,向量y∈Zmq,矩阵A∈Zn×mq,寻找一个非零向量e,满足Ae=ymodq,且 ‖e‖≤β.
1.3 格上的多项式时间算法
由于SISq,m,rm是困难的,若 A∈Zn×mq,可得格上的陷门函数[6],

其中,fA(e)=Aemodq,Dn={z∈Zn|‖e‖≤r m},Rn= Zqn,输入分布为 DZm,s.
基于原像抽样函数,文献[6]给出格上基于原像抽样的多项式时间算法:
(1)TrapGen(1n).算法 TrapGen(1n)输出(A, B),其中,矩阵 A在Znq×m接近均匀分布,矩阵B是Λ⊥(A)的小基.
(2)Sample D(A;r).从分布DZm,r中选取向量e,且fA(e)=Aemodq接近于Rn上均匀分布.
(3)Sample ISIS(A;B;y;r).输入矩阵 A ∈Zn×m,Λ⊥(A)的小基B,向量y∈Zm和r>0,qqSample ISIS(A;B;y;r)输出非零向量e,e为接近分布 DΛ⊥(A),r.
1.4 格基代理算法
格基代理算法[10]是一种由较小维数的格和基向量构造更大维数的格和基向量的算法.令 n,q, m,k为正整数,并且 q≥2,m≥5nlogq,格基代理算法ExtBasis和RandBasis描述如下:
(1)ExtBasis(S,A=A1‖A2).输入矩阵 A1∈Zqn×m,任意矩阵A2∈Znq×m1,Λ⊥(A1)的基S1,算法⊥~ExtBasis输出 Λ(A)的基 S,其中,‖S1‖=~‖S‖.
(2)RandBasis(A,S,r).输入矩阵 A ∈ Znq×m, Λ⊥(A)的基S和参数r≥‖S‖ω( nlogq),算法RandBasis输出的Λ⊥(A)的S′,其中,‖~S′‖≤r m,由S′得不到S的任何信息.
2 格上基于身份的代理环签名方案
下面主要描述利用格上的难题和格基代理技术构造基于身份的代理环签名方案.方案中的参数设置如下:令 n,q,m,k为正整数,并且 q≥2,m≥flogn,L~≥O( nlogq),r≥L~ω( logn).设 B1, B2,…,Bl为l个代理人,H1:{0,1}*→{0,1}n,H2: {0,1}*→{0,1}n×m为两个安全的Hash函数,m′= (l+1)m.
2.1 系统建立
原始签名人利用算法 TrapGen(1n)输出(A0, S0),其中,A0在Znq×m接近均匀分布,S0是Λ⊥(A0)的小基.类似的,代理人Bi利用算法TrapGen(1λ)输出(Ai,Si),Ai在Znq×m接近均匀分布,Si是Λ⊥(Ai)的小基,A0,S0分别为原始签名人公钥和私钥,Ai, Si分别代理签名人Bi的公钥和私钥.
2.2 代理密钥的生成与验证
2.2.1 代理密钥的生成.
原始签名人利用代理签名人Bi的身份信息IDi∈{0,1}*为 Bi生成代理密钥,
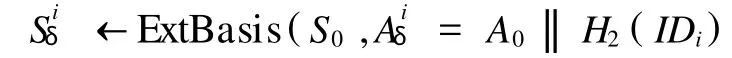
其中,Siδ为Λ⊥(Aiδ)的基.然后,将 Siδ发给Bi,i=1 ,2,…,l.
2.2.2 代理密钥的验证.
Bi验证:①Siδ∈ Z2m×kq,k=2m- rank(Aiδ);②AiδSiδ=0modq是否成立,若成立,Bi接受Siδ为代理密钥,否则,拒绝.
2.3 代理环签名的生成
l个代理签名人构成一个环,任何代理人Bi利用他的私钥Si和代理密钥Siδ均可以为原始签名人生成代理环签名.假设真正的签名人为第 k个代理人Bk,待签消息M ∈{0,1}*,签名步骤如下:
(1)由私钥Sk,Bk利用算法ExtBasis(Sk,A′δ= Ak‖A1‖‖A2‖…‖Ak-1‖Ak+1‖…‖Al)生成S′,对矩阵A′做列换,化A′为A=A1‖A2‖…‖Ak+1‖‖…‖Al,S′做相应的变换化为S,且 S为Λ⊥(A)的基.
(2)由代理密钥 Siδ,Bk利用算法 ExtBasis(Siδ, A′δ=A0‖H2(IDk)‖…‖H2(IDk-1‖H2(IDk+1)‖…‖H2(IDl))生成 S′δ,将A′δ化为Aδ=A0‖(H2(ID1)‖…‖H2(IDk-1)‖H2(IDk)‖H2(IDk+1)‖…‖H2(IDl)),S′δ做相应的变换化为 Sδ,Sδ为Λ⊥(Aδ)的基.
(3)计算y= H1(M);
(4)利用SampleISIS(A;S;y;r)生成的向量 e,若 ‖e‖≥s m′或e=0,重新生成e.
(5)利用SampleISIS(Aδ;Sδ;y;r)生成的向量eδ,若 ‖eδ‖≥s m′-1或eδ=0,重新生成eδ.
(6)Bk输出环签名(M,eδ,e,L),其中,L = {B1,B2,…,Bl}.
2.4 签名验证
验证者收到代理环签名(M,eδ,e,L)后,验证下列条件是否成立:
(1)e≠0,eδ≠0,‖eδ‖≤s m′-1,‖e‖≤s m′,
(2)(A1‖A2‖…‖Al)e=0modq,
(3)A0‖H2‖(ID1)‖H2(ID2)‖…‖H2(IDl)eδ=0modq.
若成立,验证者接受(M,eδ,e,L)为有效的代理环签名,否则,拒绝.
3 方案分析
3.1 安全性分析
3.1.1 匿名性.
签名(M,eδ,e,L)是代理环中的某个代理人利用格上一个小基和算法SampleISIS得到的向量.其中,签名过程中一个小基是代理人利用私钥通过基扩展算法生成的,具有很好的随机性,故该小基不会泄露签名人任何信息.另外,算法的构造是利用抽样算法SampleISIS得的,所得的结果(eδ,e)近似服从高斯分布,并没有泄露该小基的相关信息.由于签名结果和签名过程中小基的这两个主要信息都不会泄露签名人的任何信息,所以签名方案满足匿名性.
3.1.2 不可伪造性.
定理1 基于格上的SIS难题,本研究的代理环签名方案满足存在性不可伪造性

定理的证明分两部分,一部分是代理环签名中eδ的不可伪造性,一部分是代理环签名中 e的不可伪造性.下面仅给出第二部分证明,第一部分证明类似.
对于任意的矩阵,

其中,A1,…,Al∈Zqn×m,0 (1)1≤i≤l,令Ai为代理环中第i人的公钥; (2)l+1≤i≤Q,利用算法TrapGen(1n)输出(Ai,Si),令Ai为代理环中第i人的公钥,Si为代理环中第i人的私钥. 将环成员的公钥联立所得矩阵A1‖A2‖…‖AQ发给 F. Hash询问.对于任意的消息 mi,S随机选择ei←Sample D(AR;r),将 yi=AReimodq发送给F,并将(mi,ei,yi)存储于列表L1. 签名询问.收到 F的签名询问(j,mi,Ri),(mi, ei,Ri)若Ri=R,S在列表L1查找(mi,ei,yi),将ei返回给 F,并将(mi,ei,Ri)存储于列表L2;若 Ri≠R且l+1≤j≤Q,则S在列表L1查找(mi,ei,yi),将δi←Sample ISIS(ARi,ExtBasis(Sj,ARi),yj,r)返回给 F,并将(mi,δi,Ri)存储于列表L2;若 Ri≠R且1≤j≤l,则S在列表L1查找(mi,ei,yi),任选k∈Ri,将δi←Sample ISIS(ARi,ExtBasis(Sk,ARi), yj,r)返回给 F,并将(mi,δi,Ri)存储于列表L2. 若 F以ε的概率输出一个伪造代理环签名(j*, m*,R*,δ*),若R*≠R,S放弃;若R*=R,S在列表L1查找(m*,e*,y*),显然,y*= ARe*= ARδ*modq,若e*≠δ*,则AR(e*-δ*)=0modq,‖e*-δ*‖≤2r lm,即,e*-δ*为SISAR,lm,2r的一个解.又因为 R*=R的概率为, 所以,算法 S解决SISq,lm,2rlm的难题的概率至少为, 令m=cnlogq,其中,c为常数,l为代理环成员个数,则本研究所提出的代理环签名方案的公钥长度、代理成员的私钥长度、代理环签名长度如表1所示. 表1 本文代理环签名方案的效率分析 由表1可见:(1)与一般基于数论的代理环签名相比,本研究提出的方案设计中仅仅使用到了小整数的模加和模乘运算,所以方案计算效率较高;(2)一般的基于身份的签名方案,需要有可信中心为签名人生成签名私钥,但在本研究的签名方案中,任何签名人均可以利用格上基于原像抽样函数的算法TrapGen为自己生成签名密钥,不需要可信中心;(3)和文献[10]环签名相比,本方案的公钥长度、代理成员的私钥长度、代理环签名长度更短,整体运算效率更高. 本文利用格上的格基代理算法和原像抽样函数,在格上构造了一个基于身份的无可信中心的代理环签名方案.基于格上SIS问题的困难性,本方案满足匿名性和不可伪造性,与其他代理环签名方案相比,本方案具有在量子计算环境下依然安全的优点. [1]Shamir A.Identity Based Cryptosystems and Signature Schemes [C]//Advances in Cryptology-Crypto’84.Santa Barbara,USA: Springer-Verlag,1984:48-54. [2]Mambo M,Usuda K,Okamoto,E.Proxy Signatures for Delegating Signing Operation[C]//Proceedings of the3rd ACM Conference on Computer and Communications Security.New Y ork:ACM Press,1996:48-57. [3]Rivest R,Shamir A,Tauman Y.How to Leak a Secret Advances in Cryptology[M].Heidelberg:Springer-Verlag,2001. [4]Zhang F,Naini R S,Lin C Y.New Proxy Signature,Proxy Blind Signature and Proxy Ring Signature Scheme from Bilinear Pairings[C]//Cryptology ePrint Archive Report2003/117.http:// eprint.iacr.org/2003/104/. [5]杨少春,郎为民.基于身份和双线性对的代理环签名方案[J].微计算机信息,2006,14(12):79-81. [6]Gentry C,Peikert C,Vaikuntanathan V.Trapdoors for Hard Lattices and New Cryptographic Constructions[C]//STOC’2008. Victoria,Canada:IEEE Press,2008:197-206. [7]Alwen J,Peikert C.Generating Shorter Bases for Hard Random Lattices[C]//STACS’2009.Freiburg,Germany:IEEE Press, 2009:75-86. [8]Wang Jin,Sun Bo.Ring Signature Cchemes from Lattice Basis Delegation[J].Information and Communications Security,Lecture,2011,7043(1):15-28. [9]Peikert C.Bonsai Trees[EB/OL].[2009-07-19].http:// eprint.iacr.org.2009. [10]王凤和,胡予濮,王春晓.格上基于盆景树模型的环签名[J].电子与信息学报,2010,32(10):2400-2403.
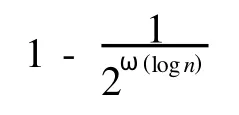

3.2 效率分析

4 结 论
