基于灰色理论的基坑变形预测预报系统研究
2012-01-10李文渊
李文渊
(成都大学城乡建设学院,四川成都 610106)
0 引 言
目前,在城乡建设中越来越多的高层或者超高层建筑需要进行深基坑的开挖.由于基坑的变形将对基坑自身稳定性和周边环境产生不同程度的影响,因此,在基坑开挖过程中应非常重视变形监测工作.但目前还没有一种成熟的方法计算基坑周围土体的位移量,岩土工程师在进行设计时通常只能借助过去的经验和工程类比,并在施工过程中通过对现场变形观测值与设计时的预测值进行对比,以验证支护结构的合理性,指导基坑开挖及支护工程施工,必要时对设计方案和方法进行调整[1-2].
由于基坑支护结构的复杂,力学机制的不清晰以及影响因素的多元化,意味着基坑的变形不能以某一种原因或因素来预测其后的变形规律.此外,影响基坑稳定的某些因素如基坑降水、自然降雨等都是未知的.据此可知,基坑工程是部分信息已知、部分信息未知的灰色系统,施工监测一般难以确定变形的发展趋势及是否需采取加固处理措施.为了根据变形监测数据进行动态设计及信息化施工,本研究拟建立灰色系统模型对基坑变形进行模拟、分析并预测其发展趋势.
1 基坑工程的灰色特性
本研究认为,基坑工程是一个灰色系统,其灰色特性主要表现在以下几个方面[3-5].
(1)土的不确定性和多样性.土是在漫长的地质年代里形成的,经历了复杂变化的过程,包括自然条件的变化和人类活动所引起的变化等.土的物质组成、组织结构特点、干湿或疏松等特性都是自然历史的产物,是在人类无力控制的条件下随机形成的,至今还没有一种理论能有效地描述这种特性.土的性状的随机不确定性还导致了地质勘探资料的不确定性.因此,实际工程中往往需要勘探工程师、设计工程师以及施工工程师根据自己的专业知识和实际经验对勘探资料进行处理.
(2)周围环境的复杂性.基坑支护体系周围环境的影响因素非常多,如地下管线、周围构筑物、道路、天气和工期等,制约着基坑支护体系.
(3)随时间的变异性.在基坑支护特有的时域内,随着基坑开挖的深入,土体的平衡被破坏,应力将重新分布,其特性随时都在变化.支护体系的位移、变形和内力也不断变化,突发事件随时可能发生.
(4)施工的随机不确定性.工程实际施工本身是一个动态过程,很难预估下阶段的实际状态,它对支护结构的影响也难了解.另外,施工过程中由于人为因素还存在着施工质量问题.
2 基坑变形灰色模型的数学基础
2.1 基坑变形灰色模型 GM(1,1)的建立
基坑变形包括支护结构水平位移、基坑周围土体下沉和坑底隆起等,对此均可通过实时监测获得其变形随时间的变化值.为模拟监测数据列的变化情况,本研究采用单序列的一阶线性动态微分方程GM(1,1)[6-7],其微分形式为,

式中,x(1)(k)为对变形监测值作1-AGO处理,即一次累加生成数列,

式中,a、b为待定系数,可用最小二乘法求得,

式中,

式中,YN为原始数列矩阵,

由式(3)求出系数向量 a、b后,代入式(1),考虑到模型的边界条件,x(1)(1)= x(0)(1),从而可得灰色预测模型G M(1,1)的离散响应为,

式中,k=0,1,2,…,n.
故,模型的预测值为,

通常,基坑变形与时间有密切关系,考虑取样时段不等对建模预测的影响,对不等时距变形时间序列的建模方法与等时段基本相同,只需对原始监测数据做加权累加生成处理,权重为不同时段Δt.
设{x(0)(k)}为一非等时距沉降观测值数列,与其相应的时刻为{tk},k=1,2,…,N,则,

做一次加权累加处理得,

灰色预测模型G M(1,1)的时间响应为,

式中,t1为初始时刻;x(0)(1)为当t=t1时的原始数据.经还原可得沉降值为,

2.2 灰色模型G M(1,1)的精度检验与修正
2.2.1 模型精度检验.
要检验G M(1,1)模型所得的预测值是否可靠,需采用检验手段.为提高预测精度,必须进行原始数据列的残差辨识,在满足要求时才能预测.对此,本研究采用关联度分析和后验差检验来保证预测的可靠性[8].
(1)灰色关联度分析.根据预测模型计算的数据列与实测数据列进行预测值曲线与实测曲线之间的灰色关联度分析,对于单序列的 x(0)和 X∧(0),在第i点的关联系数为,

式中,β为分辨系数,通常取0.5,这样,曲线 x(0)和X∧(0)的关联度为,

(2)后验差检验.记原始数据的均方差为 S1, x(0)(k)与预测值 X∧(0)(k)的残差的均方差为 S2,则,

式中,ε(0)(k)= x∧(0)(k)-x(0)(k),k=1,2,…,n;


c值越小,表明尽管原始数据很离散,而模型预测值与实际值之差并不太离散.令小误差概率 P为,

P值越大,说明残差与残差平均值之差小于给定值0.6745S1的点越多.
根据c、P这个2个指标权衡,预测值精度如表1所示.
后验差的比值定义为,

表1 预测精度表
若 P、c均在允许范围内,则可计算预测值,否则需进行残差修正,以保证预测值模型的可靠性.
2.2.2 模型修正.
经检验,如果模型不合格或勉强合格,就需进行残差建模修正.与原始数据建模方法一样,对残差序列,

有残差序列模型,

得出残差序列随时间的函数后,与式(6)还原为原始数列并相加,可得残差修正模型的还原值为,
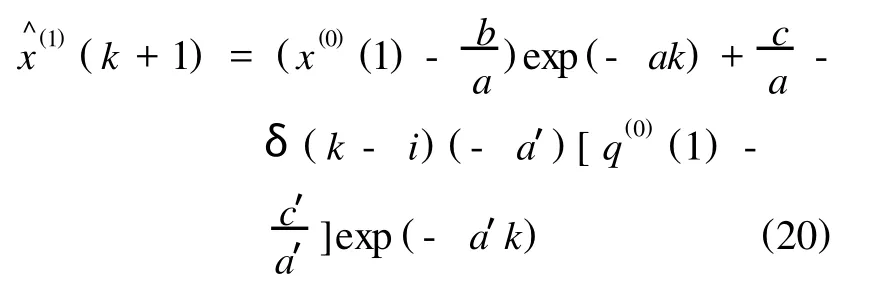
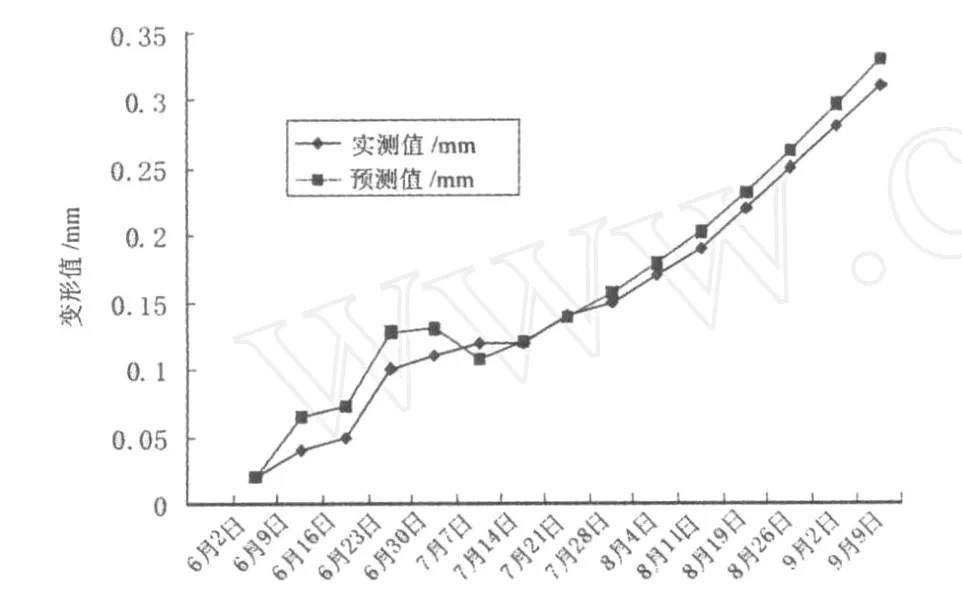
其中:δ(k-i)的值当 k≥i时为1;k 若对式(20)得出的还原值进行检验后仍未达到要求,则可进行二次残差建模,直至满足要求为止,然后进行预测. 基坑工程预测预报系统选用 GM(1,1)模型,对其建模过程、模型预测精度检验及模型修正全过程采用Fortran语言编程实现.整个基坑工程预测预报系统整体结构共由3部分组成,包括子文本、执行程序文件及使用说明.其中,执行程序文件是该预测预报系统的主要部分,该程序严格按照灰色模型 GM (1,1)的建模步骤生成,可以对预测模型进行模型精度检验与修正.其预测的具体步骤为: (1)输入观测数据及计算结果文件名(文件名的约定为***.dat); (2)观测数据文件建议用记事本按时间间距.观测次数(N)、观测数据1、观测数据2…观测数据N编录.在运行程序之前必须先把观测数据文件按要求建好; (3)输入选择数据的起点,终点及需要预报的步数; (4)在所建立的计算结果文件中打开查看预测结果. 工程实例选取成都市中心某基坑工程,该建筑地上30层,地下3层,其基坑开挖深度为16 m,周边环境较为复杂,东北两侧为道路,西侧邻近21层高层建筑,南面为多层建筑,基坑安全等级为一级.场地土层从上至下为杂填土、粉质粘土、砂卵石及强风化泥岩.基坑开挖分层进行,每层4 m,采用桩锚联合支护,每桩设有3根预应力锚索. 为确保基坑支护结构及周边建筑物的安全,基坑施工时对基坑壁土体位移及周边建筑物、道路等沉降采用全站仪进行观测,监测相隔时间为7 d.通过选取其中两个基坑位移点W3、W18及2个周边沉降点bm5、bm24的观测数据对G M(1,1)预测预报系统进行验证,并以W3点为例显示其程序运行过程(见图1、图2).选用监测数据中的前10次数据作为原始数据列进行预测,其运算结果如图3~图6所示. 图1 程序运行过程图(W3测点) 图2 程序运行结果图(W3测点) 图3 实测与预测结果变形值对比图(W3测点) 图4 实测与预测结果变形值对比图(W18测点) 图5 实测与预测结果变形值对比图(bm5测点) 图6 测点实测与预测变形值对比图(bm24) 通过对预测数据进行检验,发现预测数据的预测精度能较好地满足预测要求,因此没有对预测模型进行修正.从预测结果可知,该预测预报系统具有较好的拟合度和预测可靠性,能提前预测位移,并提前做出预警,对指导基坑开挖及支护工作有很好的意义.随着位移监测资料的增加,系统能及时地对多个监测点实现动态模拟预测. 本预测预报系统在该基坑工程中的成功运用及施工管理人员共同的努力下,该基坑开挖施工未对周边环境和地下室结构施工造成不良影响,基坑开挖施工成功完成并已回填. (1)应用灰色系统理论所建立的基坑变形预测预报系统来处理和分析基坑变形观测是完全可行的,且精度较高,大多情况下可以达到90%以上,完全满足工程需要.针对基坑工程原始数据少的特点,仍能对基坑开挖变形进行较好的预测;在数据量较大(一般相应于观测数据10个以上,预测相对误差一般<10%)时,可以利用预测结果进行险情分析判别和进行长期预测.这为处理和统计变形观测数据及精度分析提供了一种新的方法. (2)该模型可通过残差大小、关联度检验、后验差检验等多种检验方法来分析和提高预测结果的准确性. (3)从变形实测值和预测值能看出,该预测预报系统对近、中期是比较准确的,预测精度满足要求,但预测的精度在预测数据的后期较差.因此,在运用本预测预报系统时,应尽量选用最新的数据,且预测步数不宜过长. (4)在基坑变形预测预报中,雨天和周边地区有较大的震动以及有周围环境发生较大变化时,应缩短观测周期,增加观测次数,以便在施工中及时发现异常,确保变形观测真正起到预防和预报作用. [1]王玲玲,刘汉东,谢英.深基坑变形的灰色预测模型[J].华北水利水电学院学报,1999,20(3):41-43. [2]Liu zhibin.The Settlement Prediction of Deep Excavation Based on Gray Markow Chain Model[J].Geology&Exploratioin 2002, 11(6):35-38. [3]朱玉平,黄涛.基坑变形的灰色模拟与预测[J].广东土木与建筑,2000,28(4):19-23. [4]廖野澜,谢谟文.监测位移的灰色预报[J].岩石力学与工程学报,1996,15(3):269-274. [5]Whiffle A J,Hashash Y M A.Soil Modeling and Prection of Deep Excavation Behavior Whittle[M].Califina:Failure Deform charact Geomaterial,1994. [6]邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1990. [7]邓聚龙.灰色预测与决策[M].武汉:华中理工大学出版社,1986. [8]Huang Mint,Liu Jun,Ge Xiurunl.Prediction of Resolution and Homposition of Measured Displacement During Slope Excavation [J].Chinese Journal of Rock Mechanics and Engineer,2003,19 (8):1320-1323.3 基坑工程预测预报系统程序的实现
4 工程应用





5 结 论
