复合算子G·T的Poincaré型加权积分不等式
2012-01-09李华灿邹翠
李华灿,邹翠
(1.江西理工大学理学院,江西赣州341000;2.南昌陆军学院科文教研室,南昌330103)
复合算子G·T的Poincaré型加权积分不等式
李华灿1,邹翠2
(1.江西理工大学理学院,江西赣州341000;2.南昌陆军学院科文教研室,南昌330103)
利用C.Scott,T.Iwaniec与A.Lutoborski等人的有关结论得到了有界域Ω上关于Green算子G和同伦算子T的复合算子G·T的Poincaré-型不等式,进而通过令u=d*v得到作用于共轭A-调和张量的复合算子G·T的Poincaré-型不等式.在此基础上,得到加权Poincaré积分估计式.
积分不等式;复合算子;共轭A-调和张量;有界域;加权
0 引言与预备知识
Poincaré不等式是一个非常有趣且重要的课题,近年来,在此领域的研究已经取得了丰硕的创新性成果:Wing-Sum Cheung于1993年得到了有关Poincaré型积分不等式[1],2001年证明了几类特定形式的Poincaré不等式[2];2006年包革军教授[3]证明了关于微分形式的双权Poincaré不等式;2007年王勇[4]证明了在LS(μ)-平均域上微分形式的双权Poincaré型积分不等式,更多有关Poincaré不等式的成果,详见文献[5-7].了解Poincaré不等式的有关成果对进一步研究解析函数的性质[8]很有帮助,因此对Poincaré不等式的研究很有必要.文中研究了有界域Ω上作用于共轭A-调和张量的复合算子G·T的Poincaré-型不等式.
全文假定Ω为Rn中连通开子集,设e1=(1,0,…,0),e2=(0,1,…,0),…,en=(0,0,…,1)为Rn上标准正交单位向量组,用Λl=Λl(Rn)表示由外积eI=ei1∧ei2∧…∧eil所生成的l维线性向量空间,其下标所对应的有序l-丛I=(i1,i2…,il),1≤i1≤i2≤…≤il≤n,l=1,2,…,n.对于α=∑αIeI∈Λ及β=∑βIeI∈Λ,称<α,β〉=∑αIβI为α与β的内积,其中对所有的有序l-丛I求和.Hodge星算子*:Λ→Λ由规则*1=e1∧e2∧…∧en和α∧*β=β∧*α=<α,β〉(*1)确定,其中α∈Λ及β∈Λ.
Ω上的l-形式ω是一个Ω上取值于Λl(Rn)的Schwartz分布,D'(Ω,Λl)为所有的l-可微形式空间,将Ω上对所有有序l-丛I满足形式:

记为Lp(Ω,Λl),其中ω是权函数.从而Lp(Ω,Λl)成为范数如下的Banach空间:

类似地,W1,p(Ω,Λl)为所有Ω上的系数属于W1,p(Ω,R)的微分l-形式集.外导数d∶D′(Ω,Λl)→D′(Ω,Λl+1)的形式共轭算子d*∶D′(Ω,Λl+1)→D′(Ω,Λl)由定义在D′(Ω,Λl+1)上的d*=(-1)nl+1*d*给出.
称下面的非线性微分方程

为共轭A-调和方程,其中A∶Ω×Rn→Λl(Rn)对几乎所有的x∈Ω以及所有的ξ∈Λl(Rn)满足:这里α〉0,1 定义1如果u和v在有界域Ω上满足共轭A-调和方程A(x,du)=d*v且A-1存在,则称u和v是Ω上的共轭A-调和张量. 并且有如下分解式ω=d(Kyω)+Ky(dω).利用上面给出的线性算子Ky,来定义同伦算子 对每一个坐标系,如果u的坐标函数的逆在相似意义下也有一个广义梯度,其中则说u有一个广义梯度[10],记为: W(Λk,Ω)一个广义梯度} 通常把一个调和k场定义为: K(Λk,Ω)={u∈W(Λk,Ω)∶du=d*u=0,u∈Lp,其中1 下列有关调和l-场的性质出现在文献[11]中. 性质1K(Λl,Ω)C∞(Λl,Ω). 性质2对任意的u∈L1(Λl,Ω)存在唯一一个H(u)∈K,使得: 对任意的h∈K成立. 定义2设u∈L1,用H(u)来记由性质2确定的中的K唯一元素,并称H(u)为调和投影或u的调和部分. 在给出投影算子H的定义后,Green算子的定义为: 并且G(u)是K⊥∩C∞中满足Possion方程的ΔG(u)=u-H(u)唯一元素. 为了得到Lp上Green算子的定义,需要讨论2≤p<∞和1 的唯一元素,其中u∈K⊥∩Lp. 定义3当p≥2时,定义Green算子G为 定义4当1 由定义知G为W2,p中的有界线性算子. 1995年,C.Scott证明了下面的引理,它将在下面的证明中用到. 引理1[12]设u∈C∞(Λk,Ω),l=0,1,…,n.若1<s<∞,则存在与u无关的常数C,满足: 1993年,T.Iwaniec与A.Lutoborski给出了下面关于微分形式的嵌入不等式. 引理2[13]分形式,其中1<s<∞且l=0,1,…,n,则有 结合引理1与引理2,便可得到如下的关于Green算子G和同伦算子T的复合算子G·T的Poincaré不等式. Poincaré-型估计式(1)可以等价地描述为: 证明:由引理1及引理2可得 故而由ω=d(Tω)+T(dω)知 在定理1中令u=d*v,便可得到以下作用于共轭A-调和张量的复合算子G·T的Poincaré-型不等式: 推论1设u和v是有界域Ω上共轭A-调和张量,则存在不依赖于u和v的常数C,满足: 文中将用到下面关于d*v的逆Ho¨lder不等式. 引理3设u和v是Ω上共轭A-调和张量,0 这里σQ_ Ω. 引理4[14]设u和v是Ω上共轭A-调和张量,则存在不依赖于u和v的常数C1,C2,满足: 由引理4很容易得出以下推论: 推论2设u和v是Ω上共轭A-调和方程的解,则存在不依赖于u和v的常数C1,C2,满足: 这里D_Ω,α〉0,ω为任意权函数. 下面给出著名的Muckenhoupt权的定义. 这里球体Q_Ω,r〉1. 在文中的证明中将用到Ar(Ω)-权的下列性质: 引理5[15]如果ω(x)∈Ar(Ω),则存在不依赖于ω的常数C,满足: 其中球体Q_Ω,β〉1. 定理2设u和v是Ω上共轭A-调和张量,则存在不依赖于u和v的常数C,满足: 其中ω(x)∈Ar(Ω),σ〉1且σQ_Ω,r〉1,0<α≤1,1+α(r-1) 证明:首先,假设0<α≤1,令s=q/(1-α),由广义Ho¨lder不等式可得: 选取t=q/(α(r-1)+1),则t 因为t 综合式(6)~式(8),便有: 由于ω(x)∈Ar(Ω),于是有: 把式(10)代入式(9)中可得: 由推论2及式(11)可知: 故当0<α≤1时,定理2结论成立. 下证当α=1时,定理2结论也成立. 由引理5知,存在β〉1和C7〉0使得: 令t=q/r则t<q,综合引理3及式(3),便有: 由广义Ho¨lder不等式可得: 综合式(15)与式(16)可知: 由于ω(x)∈Ar(Ω),于是有: 把式(17)代入式(14),并使用式(18),便有: 结合推论2与式(19),可得: [1]Wing-Sum Cheung.Some new Poincaré-type inequalities[J].Bulletin of The Australian Mathematical Society,2001,63(2):321-327. [2]B G Pachpatte.On Poincaré-type integral inequalities[J].Journal of The Mathematical and Application,1986,114(1):857. [3]Bao G J.Two-weighted Poincaré-Type integral inequalities[J].Proceedings of the Conference on Differential&Difference Equations and Applications,2006:141-148. [4]Wang Yong.Two-weight Poincaré-Type for differential forms in LS(μ)-averaging domains[J].Applied Mathematics Letters,2007(11):1161-1166. [6]Ding S S,Xing Y M,Bao G J.Ar(Ω)-weight inequalities for A-harmonic tensors and related operators[J].Journal of Mathematical Analysis and Applications,2006(1):219-232. [7]G R Nicklason.A general class of centers for the Poincaré problem[J].Journal of Mathematical Analysis and Applications,2009(1):75-80. [8]李晓昭.某类解析函数的一些性质[J].江西理工大学学报,2009,30(1):53-55. [9]Craig A.Nolder.Hardy-littlewood theorems for A-harmonic tensors[J].Illinois Journal of Mathmatics,1999(4):613-631. [10]Shusen Ding.Some examples of conjugate p-harmonic differential forms[J].Journal of Mathematical Analysis and Applications,1998(1):251-270. [11]Morry,Charles B.Mutiple integrals in the calculus of variayions[M].Berlin Heidelberg New York:Spring-Verlag,1966. [12]Chad Scott.Lp-theory of differential forms on manifolds[J].Transactions of American Mathmatical Socieety,1995(6):2075-2096. [13]Tadeusz Iwaniec,Adam Lutoborski.Integal estimates for null lagrangians[J].Arch Rational Mech.Anal.1993(1):25-79. [14]Shusen Ding.Local and global norm comparison theorems for solutions to the nonhomogeneous A-harmonic equation[J].Journal of Mathematical Analysis and Applications,2007(2):1274-1293. [15]J Heinonen,T Kilpelainen,O Martio.Nonlinear potential theory of degenerate elliptic equations[J].Oxford,1993. The weighted Poincaré integral inequalities for the composite operator of G and T LI Hua-can1,ZOU Cui2 (1.Faculty of Science,Jiangxi University of Science and Technology,Ganzhou 341000,China;2.Department of Science and Culture,Nanchang Army College,Nanchang 330103,China) Based on the work of C.Scott,T.Iwaniec and A.Lutoborski etc.,the Poincaré inequalities for the composite operator of G and T on the bounded domain are obtained.Then the Poincaré inequalities for the composition of G and T acted on the conjugate A-harmonic tensors by selecting u=d*v are achieved.The weighted Poincaré integral inequalities are gained. integral inequality;composite operator;conjugate A-harmonic tensors;the bounded domain;weighting O175.2 A 2012-08-28 江西省教育厅基金项目(GJJ12356) 李华灿(1985-),男,助教,主要从事调和分析等方面的研究,E-mail:hua03010217@126.com. 2095-3046(2012)05-0097-04


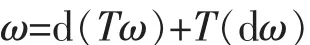
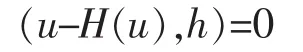


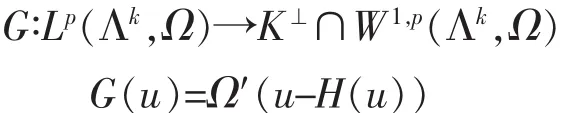

1 关于复合算子G·T的Poincaré-型估计


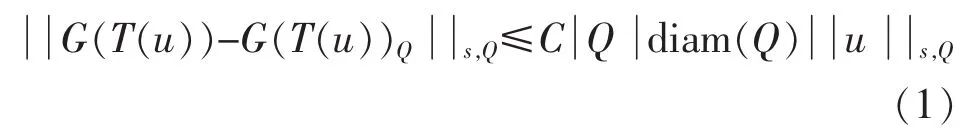




2 Ar(Ω)-权Poincaré-型估计






















