双元计算法求体积本征值
2012-01-05吉紫娟包佳祺靳海芹肖明
吉紫娟,包佳祺,靳海芹,肖明
(1.湖北第二师范学院理论物理研究所,湖北 武汉 430205;2.华中科技大学文华学院光信息科学与技术系,湖北 武汉 430074)
目前,圈量子引力取得的主要成果之一是空间的量子化.利用使空间量子化的自旋网编织空间,以及由自旋网产生的黑洞表面量子化面积与黑洞辐射等的研究,在Hamilton动力学的研究中得到的时空泡沫理论,也为时间的量子化提出了模式.对于空间的量子理论,其成果主要集中在面积与体积的量子化研究上,目前这方面已经取得了完整的结果,并在理论本身以及黑洞量子行为等研究上,做出了理论预言.在空间量子化的具体计算上,存在着不同的方法,它们都能说明量子化的基本原理的正确,而所带来的不同,则体现了不同方法的特色[1].本文中用抓算符直接抓在圈线上的方式,并采用Penrose的双元恒等式进行计算,给出一种体积量子化方法.该方法可以求出任意价顶角的体积,并且可以应用到求面积的本征值中,使圈量子引力中求面积、体积本征值的方法达到统一[2].
1 体积算符及其对自旋网的作用原理
1.1圈变量表示的体积算符在介绍双元计算方法之前,首先给出体积算符的定义及其作用的一般原则[3].体积算符与面积算符一样,也应当与背景无关,而且它们的作用结果应当是得到有限的期望值和微分同胚不变的.本文利用体积表式:

(1)
来计算体积.由该体积表式出发,可用与背景无关的体积算符的正规化手段,得到空间体积量子化的期望值.为此,定义带有3个抓的圈变量:

(2)
式中,α为连接s和t的直线段.从而,当圈α缩成一点x时,可得:
(3)
由于(3)式的存在,使得用圈变量Tabc[α]代替微体积平方算符对自旋网顶角的作用成为可能,现在考虑“密度”:

(4)
式中,αστρ为一个三角圈,它的3个点σ,τ,ρ连接在微立体RIε的3个积分表面上,DIε相当于微立体体积密度的平方.
对于量子化的体积算符,有如下表式:

(5~6)
上式中的微体积密度,将通过如下带有圈变量的形式给出:
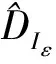
(7)

(8)
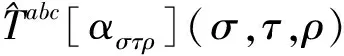
圈αστρ上的抓三重组(σ,τ,ρ)抓在 (9) (9)式为空间∑中的体积算符对自旋网态作用的本征方程,它规定了算符作用的一般原则.该式对自旋网S的任何顶点的任意3-顶角展开的任何着色均适用. (10) (11) (12) 2.13价顶角的体积谱通过3-顶角的圈线,抓三重组对3-顶角作用时,只有3种不同线型.将3种线型贡献的抓法数加在一起,经计算,其和为p1p2p3.令p1p2p3=G3,G3为顶角抓法数,将其代入(12),得到3-顶角的体积谱为: (13) 式中,p1,p2,p3为毗邻3-顶角的三条腿的颜色. 2.24价顶角的体积谱对一个4-顶角求体积,首先将其进行3-顶角展开,得到一个确定的3-顶角展开图,如图1: 图1 4价顶角的3-顶角展开 图2 4价顶角含对穿圈线的网结 对于4-顶角,抓作用的腿型只有(■-■-■)一种,抓三重组抓住通过邻腿的圈线时对着色抓法数的贡献为: (14) 而抓住含有对穿圈线时对着色抓法数的贡献为: B4=2(i24p1p3+i13p2p4)+i13[(i23+i34)p1+(i12+i14)p3]+i24[(i34+i14)p2+(i12+i23)p4]+ (15) (16) (17) 图3 5价顶角的3-顶角展开 图4 5价顶角圈线走向图 抓三重组在5-顶角的3条腿上,共有(■-■-■)和(■-■,■)两种腿型作用.经过计算,分别得到5-顶角腿型(■-■-■),不含与含诸对穿线的情况下对着色抓法数的贡献A5,B5如下: (18) (19) 而5-顶角腿型(■-■,■),通过5种抓法实现,这5种抓法抓在圈线上时对着色抓法数的贡献为:C5=p1p2p4+p2p3p5+p3p4p1+p4p5p2+p5p1p3 (20) (21) (22) 本文中利用将几何算符中的抓,直接抓在自旋网的圈线上的方法,得到了3,4,5价顶角的体积算符的期望值.在演算过程中,除利用了抓作用使圈线反对称外,只采用了Penrose双元恒等式.其结果是,所有类型抓作用均为具有同一本征值的本征作用.存在于空间中的自旋网,在经历所在空间的区域在顶角上施加的算符作用后,仍保持不变.从而,所有抓三重组作用的全部本征值的求得,将最后归结为对顶角抓法数的求得,这是一个重要结论.利用双元计算法得到的本征方程是个代数方程,与国外利用图式算法求解比较,将更方便,更接近体积算符实际情况.利用该方法还可求得6-顶角或更高价顶角的体积.此外,这种方法不仅可以求得体积的本征值,还可应用到求面积本征值,使圈量子引力中,求面积、体积本征值的方法达到统一,并且还可用于微分同胚约束和Hamilton约束的计算[5]. [1] C Rovelli and L.Smolin,Discreteness of area and volume in quantum gravity[J].Nucl Phys B,1995,442:593-622. [2] 邵丹,邵亮,邵常贵,等.自旋结网圈表象中体积与面积本征值[J].物理学报,2005,54(10):4549-4555. [3] Loll R,The volume operator in discretized quantum gravity[J]. Phys Rev Lett,1995,75(17):3048-3051. [4] Loll R,Spectrum of the volume operator in quantum gravity[J].Nucl Phys B,1996,460:143. [5] 包佳祺,吉紫娟,肖飞.圈量子引力中面积算符的本征值[J].武汉理工大学学报:自然科学版,2010,32(8):133-135.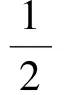
2 3价顶角、4价顶角及5价顶角的体积
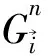



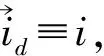

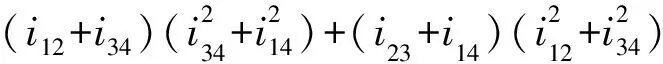

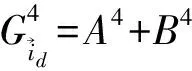
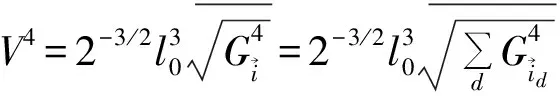




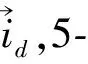

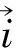
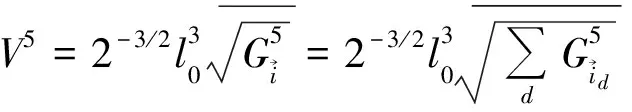
3 结语
