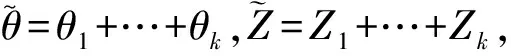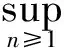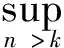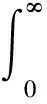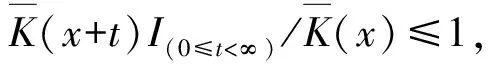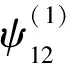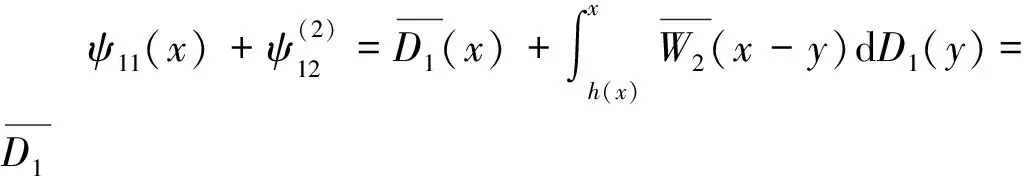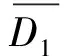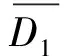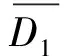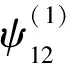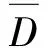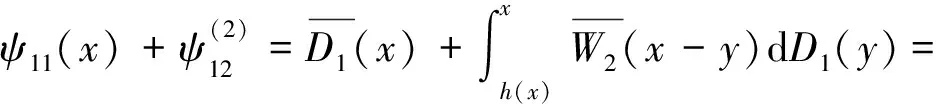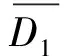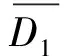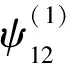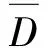多重延迟复合更新风险模型中的局部破产概率
2012-01-05万成高
万成高
(湖北大学数学与计算机科学学院,湖北 武汉 430062)
0 引言
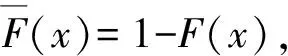
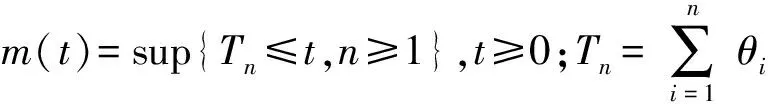
(1)
其中常数c(0 (2) 这里x≥0代表保险公司初始资本. (1)S*={F: 对任意的γ≥0,有Sd(γ)⊂S(γ)⊂L(γ).但当γ>0时,由文献[3]知F∈Sd(γ) ⟺F∈S(γ). 在保险公司的日常运营中,由于种种原因,总会有几次发生索赔的时间间隔特殊,不妨假设是前有限次,因此有一些问题就不能按通常的方法来处理.为此建立下述模型,来研究这些情况对我们关心的破产问题所产生的影响. 到时刻t为止的风险过程{S(t):t≥0)}定义为 (3) (4) 若k≥2,则称上述模型为随机多延迟复合更新模型;若k=1,则称上述模型为一重延迟更新风险模型,即平常所说的延迟复合更新风险模型;若k=0,则上述模型即为普通复合更新风险模型. (5) 用D+来表示R(N1)-R(k)的分布,令f+,g+分别为R(N1)-R(k)的F-S变换和L-S变换,即 定理1在ρ1>0的多重延迟复合更新风险模型中,若索赔额分布F∈S*,则对任意z>0有 (6) 定理2在ρ1>0的k重延迟复合更新风险模型中,若B<∞,-γ是fD(iλ)的收敛域的左横坐标,若γ>0及fD(-iγ)<1,则下列关系成立D∈S(γ)⟺D+∈S(γ)⟺W∈S(γ) (7) (8) 其中C2s=C2,s-1fD1(-iγ)+(W2(0)+gW2(-γ))gG1(cγ)(gG(cγ))-1,s=1,2,…,k,及C20=C2. 定理3在ρ1>0的k的重延迟复合更新风险模型中,若B<∞,-γ是fD(iλ)的收敛域的左横坐标,若γ>0及fD(-iγ)<1,则F∈Sd(γ)⟺K∈S(γ)⟺D∈S(γ)⟺D+∈S(γ)⟺W∈S(γ) (9) (10) 引理1[4]对某个γ≥0,F∈L(γ)当且仅当H(F,γ)≠Φ. 引理5对任意γ≥0,已知μ1(γ)<∞,如果F∈Sd(γ),那么也有K∈Sd(γ). 引理5的证明因为有 (11) 根据重尾族Sd(γ)的定义,便可知K∈Sd(γ).而对v≤x/2,有 (12) 从而由控制收敛定理得 (13) 另一方面,再由F∈S(γ)和控制收敛定理知 (14) 综合(12)式及(13)式就有 (15) 再来证明I2→0.由(14)式可知存在一个ε>0,使得 从而就有 所以 (16) 联合(12)式,(15)式以及(16)式就有(11)式成立,即K∈Sd(γ). (17) 并且 K∈S(γ)⟺D∈S(γ) (18) 故(17)式成立,由引理3知H(K,γ)=H(D,γ),从而据引理1有D∈L(γ),那么,再由引理2易见(18)式成立. 补救措施:如果在实际施工中遭遇锤头掉落的现象,则需要现场有经验的技术工人用自制的打捞钩打捞,在打捞钩使用前必须仔细检查是否有尖锐突起或者尖利面,以免在打捞时对安全绳造成破坏,造成不可挽回的损失。 所以 W1(x,x+z]=W1(x+z)-W1(x)= (19) 显然 上述最后一项是因为当F∈S*=Sd(0)时,由引理5可知K∈Sd(0)=S*⊂S,故据控制收敛定理可得 (20) (21) (22) (23) 先看I12,由(22)可知 再看I11,由(21)式有 (24) 定理2的证明我们用数学归纳法来证明,仍沿用前面的记号,则 由引理6,只须证明(8)式中的第一个渐近关系成立. 先证k=1时(8)式成立.已知K∈S(γ),由引理6及文献[7]易知Dj∈S(γ),j=1,…,m.D∈S(γ),D+∈S(γ)及W∈S(γ).注意到此时M2中没有延迟.因此,由D∈S(γ)及文献[7]就有 (25) 任取h∈H(D,γ)=H(W∈,γ),我们用此h将ψ12(x)分解成如下形式: (26) 则由(25)式,有 (27) 仍由(25)式及fD(-iγ)<∞知,gW2(-γ)<∞.由分部积分,W2∈S(γ),D1∈S(γ),我们有 (28) 联合(27)式和(28)式得 即当k=1时,(8)式成立. 现假设k=s时,(8)式成立,即M中正好有s个延迟,则 (29) 仍由分部积分,W2∈S(γ)及D1∈S(γ),我们有 (30) 再结合(29)式及(30)式,可得 即k=s+1时,(8)式也成立,这就完成了定理2的证明. 定理3的证明在引理5中,已证当F∈Sd(γ)时, 也有K∈S(γ),从而K∈S(γ),再由引理6就得到K∈S(γ)⟺D∈S(γ),根据文献[7],从而有(9)式成立. 引理6的(17)式进一步说明了(10)式是成立的,因此完成了定理3的证明. [1] Tang Q H,Su C,Jiang T.Large deviations for heavy-tailed random sums in compound renewal risk model[J].Prob Stat Letters,2001,52(1):91-100. [2] Embrechts P,Klupeberg C,Mikosch T.Moedlling extremal events for insurance and finance[M].Berlin:Springer,1997. [3] Klüppelberg C.Subexponential distributions and characterizations of related classes[J].Prob Th Rel Fields,1989,82:265-269. [4] Klüppelberg C.Subexponential sisributions and integrated tails[J].Appl Prob,1988(1):132-141. [5] Kong F C,Cao L,Wang J L.Ruin probabilities for large claims in compound renewal risk model[J].Coll Math,2005,21(3):6-12. [6] Asmussen S,Kalashnikov V.A local limit theorem for random walk maxima with heavy tails[J].Stat Prob Lett,2002,56:339-404. [7] Wang Y B,Cheng D Y.Local ruin probability in the delayed renewal risk model with large chaims[J].Chinese Journal of Appl Prob and Stat,2006,22:4-10.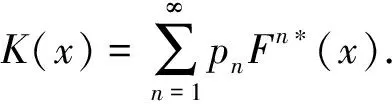
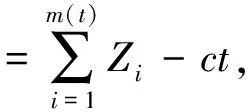
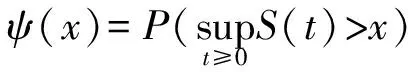
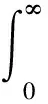

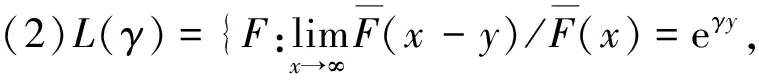
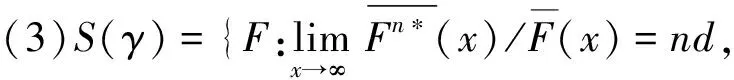

1 模型与主要结论
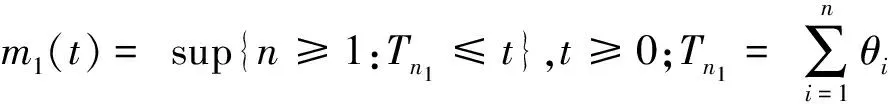
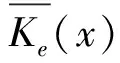
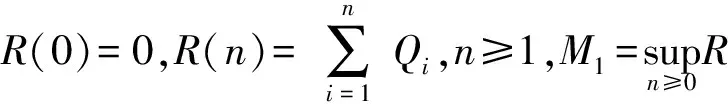
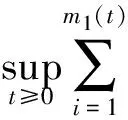
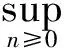
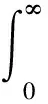
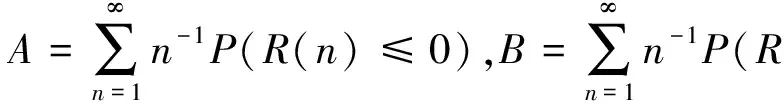
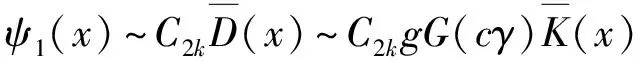
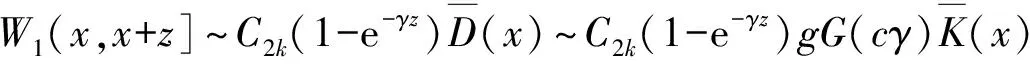
2 几个定理
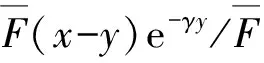
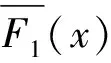
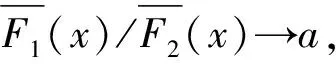

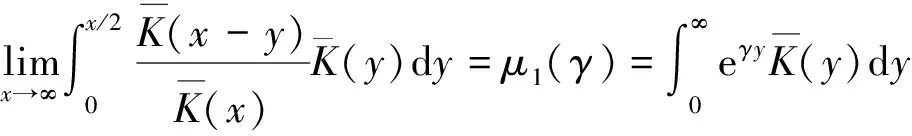
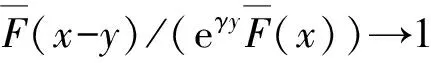
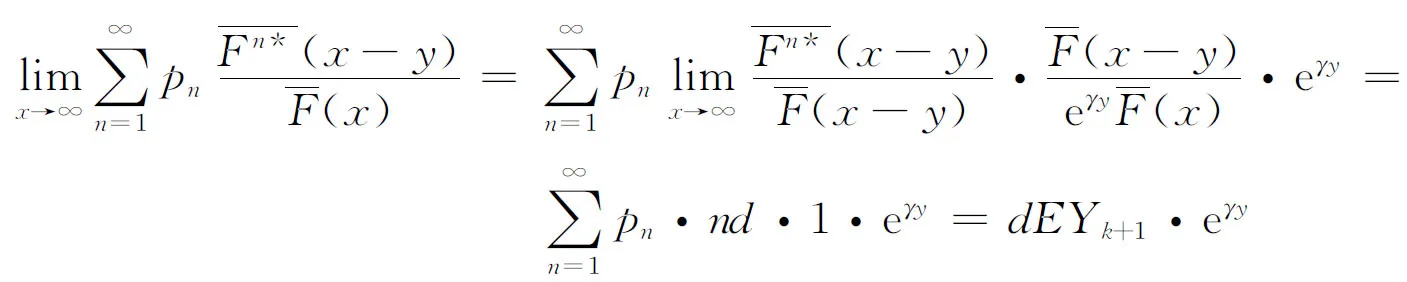
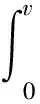
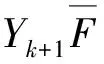
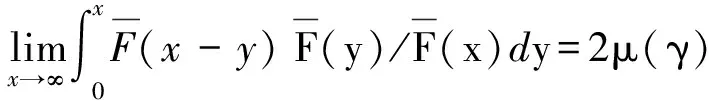
3 定理的证明