罩式退火过程中的多吊机调度问题
2012-01-04李彦平
谢 谢,李彦平
(沈阳大学 辽宁省装备制造综合自动化重点实验室,辽宁 沈阳 110044)
罩式退火过程中的多吊机调度问题
谢 谢,李彦平
(沈阳大学 辽宁省装备制造综合自动化重点实验室,辽宁 沈阳 110044)
研究了钢铁企业罩式退火中的多吊机调度问题,目标函数是最小化最后一个板卷的退火完工时间.通过考虑机器和吊机位置,建立了混合整数规划模型,并提出了一种整合的方法以降低问题的难度同时保持问题的本质.然而,即使是整合后的问题也是强NP难的.进一步提出了包括分配和调度的两阶段启发式算法.在分配阶段,利用动态规划先将每个吊机分配给唯一的子区块,再进行机器的分配.调度阶段采用最早需要操作阶段优先的策略.最后,算法的有效性通过绝对性能分析的角度给出了估测.
吊机调度;罩式退火过程;强NP难;启发式;绝对性能分析
罩式退火过程是钢铁企业冷轧板卷后道工序生产常见的模式.通常三四个板卷预先组成一垛,每垛板卷需要经过先加热后冷却的生产阶段.加热阶段需要使用的工具为加热罩,冷却阶段需要使用的工具为冷却罩.两种工具的数量都是有限的.本文将每垛板卷定义为一个工件.罩式退火车间通常由若干矩形的区组成,在每一区内,炉台按照它们的坐标排列.在区的上方,有两个或多个吊机同时操作,如图1所示(图中的符号将在后面解释).本文提出并分析了一个多吊机调度的模型,同时考虑分配和调度有限的加热罩、冷却罩,以使一个区内工件的最大完工时间最小化.
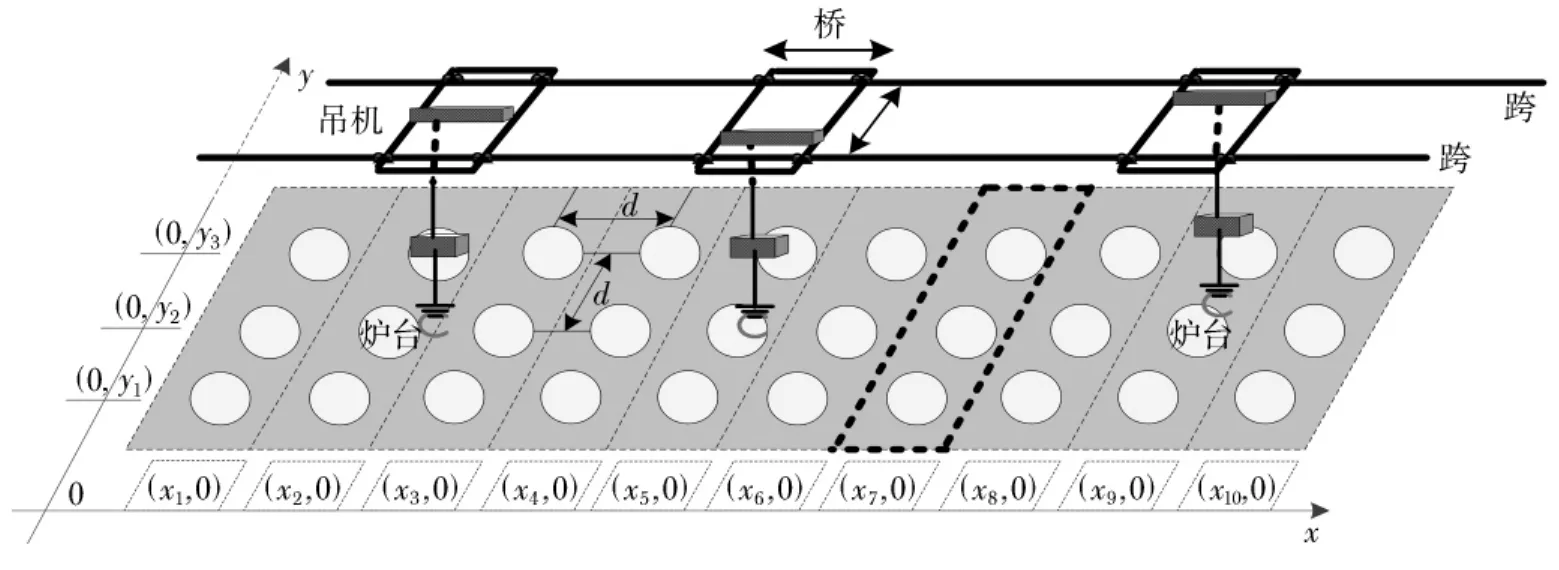
图1 罩式退火车间内一个R=10和L=3区域的图例Fig.1 Case diagram of an area with R=0 and L=3 in batch annealing workshop
每个板卷的退火过程需要在固定炉台上进行,从装炉到卸载必须经过12个阶段,这12个阶段为一个退火周期.退火周期各阶段如下:■装板卷和对流板;①装内罩;②自然充气;③装加热罩;④加热;⑤卸加热罩;⑥自然冷却;⑦装冷却罩;⑧强制冷却;⑨卸冷却罩;⑩卸内罩;○11卸板卷和对流板.
在所有阶段中,除第2阶段(自然充气)、第4阶段(加热)、第6阶段(自然冷却)和第8阶段(强制冷却)外,其余都需要上方的吊机的装载或卸载.装载一台工具可以看做由吊机进行的连续操作:吊机从当前位置提起工具,带着它一起移动直到将它放置在另一炉台上.如果没有其他炉台需要这个工具,吊机将它提起后直接放在当前炉台旁边即完成卸载.
基于上面的问题描述,根据生产实际,所提出的主要假设如下:
(1)每垛板卷必须分配给每个炉台.对流板数量充足,放在每个炉台旁边.每个炉台与内罩一一对应.
(2)每垛板卷加工的12个阶段必须在一个炉台上进行.
(3)自然充气和自然冷却的时间不是严格的确定时间,除此之外,其余各阶段的时间均为确定值,并预先已知.
(4)吊机在两个炉台之间的运输时间可以确定.
(5)各设备在加工过程中没有故障.
(6)板卷、各种罩以及吊机在零时刻之前不可获得.
(7)直到加热或冷却阶段停止时,吊机才允许卸罩或装罩.
(8)所有的加热罩(冷却罩)都是相同的.
现有的关于吊机调度的研究主要处理两方面的问题:电镀生产线的吊机调度问题和集装箱终端的岸吊或场吊调度问题.在电镀生产线中,无论是单吊机调度问题还是多吊机调度问题,大部分的研究主要集中在决策最优周期的问题[1-3].Lee等[4]、Hall等[5]、Mak等[6]和 Crama等[7]分别给出了相关的综述,几乎所有的调度过程都是周期性的.另一方面,在集装箱终端,大部分的研究主要侧重于从计算智能的角度对吊机调度问题进行研究[8-12],几乎没有从理论分析的角度对算法的性能进行证明.以上文献中的吊机调度没有可直接应用于钢铁企业中的吊机调度.此外,已有文献对问题的一些额外特点,如工件固定不动、每个工件需要吊机多次操作以及无周期的目标函数均没有进行研究.本文的研究可以看做结合了吊机调度和工具分配,而在以前的研究中,这两者是相互独立的.这种包含调度和分配本质上增加了问题的复杂性.在过去的十多年中,尽管罩式退火过程受到了Moon和Hrymak[13]的关注,然而他们的研究侧重于工件的加工而忽略了吊机的移动、上提下放时间,即使在最简单的假设下,也很少对这个调度问题提出理论模型并进行分析.因此,本文一方面通过理论分析对这个实际问题进行了更清楚的研究,另一方面提出了有效的启发式算法,为实际问题提供更快、更近似的解.
1 问题模型和分析
1.1 问题参数
给定n个工件的集合Ω={1,2,…,n},每个工件已经预先放在装载区域上.每个炉台位置固定并按照坐标排放.鉴于加工过程中工件与炉台之间的一一对应,工件i的位置可以表示为w i=(x i,y i)(∀i∈Ω)(如图1所示).同一行或列中相邻两炉台之间的距离为d.
给定两类工具的集合F和C,分别表示加热罩和冷却罩的集合.每个集合的基数为|·|.工具的位置等于与它距离最近的炉台的位置.
给定吊机的集合M,这些吊机共享同一跨,从左至右分别表示为1,2,…,|M|.为了避免碰撞,相邻的吊机之间必须至少保持一个安全距离d.吊机的位置等于吊钩向地面的投影与之距离最近的工件位置.
吊机从炉台上提或者下放一台工具到炉台的时间为μ(本文可以很容易扩展为上提和下放时间不同的情况).吊机带着工具运行的速度为v,空运行的速度为λ(λ≥v).
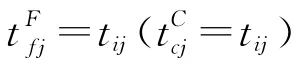
定义吊机操作阶段的集合S={0,1,3,5,7,9,10,11}和两个加工阶段的集合S′={4,8},其中,4和8分别代表加热和强制冷却阶段.此外,自然充气和自然冷却的集合可以表示为S″={2,6}.对于一个工件的任意阶段b,q∈S∪S′∪S″,b<q意味着b必须在q之前进行.
令Cmax(σH)为由算法H得到的调度σH的最大完工时间,Cmax(σ*)为最优调度σ*的完工时间.如果对于问题的任意一个例子,都有Cmax(σH)-Cmax(σ*)≤α成立,那么算法H的绝对性能比为α.
(1)输入数据如下.
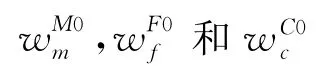
p is,∀i∈Ω,工件i在第s阶段的处理时间.除第3,5,7,9需要在调度阶段进行决策外,其他的都是预先给定的.
A,一个非常大的正数.
(2)决策变量如下.

zipjq∈{0,1},∀i,j∈Ω,∀p,q∈S∪S′∪S″,如果工件j的第q个状态在工件i的第p个状态完成后开始,那么zipjq=1,否则zipjq=0.
p i3,p i5,p i7和p i9等于工件间总的转移时间,这个时间依赖于它们的位置和上提与下放时间的总和.
Dip,∀i∈Ω,p∈S∪S′∪S″,工件i的p个状态的完工时间.


1.2 问题模型
根据上面定义的各变量,问题可以表述成一个混合整数规划模型.当相邻两个吊机同时操作时,需要考虑吊机间的不碰撞约束.
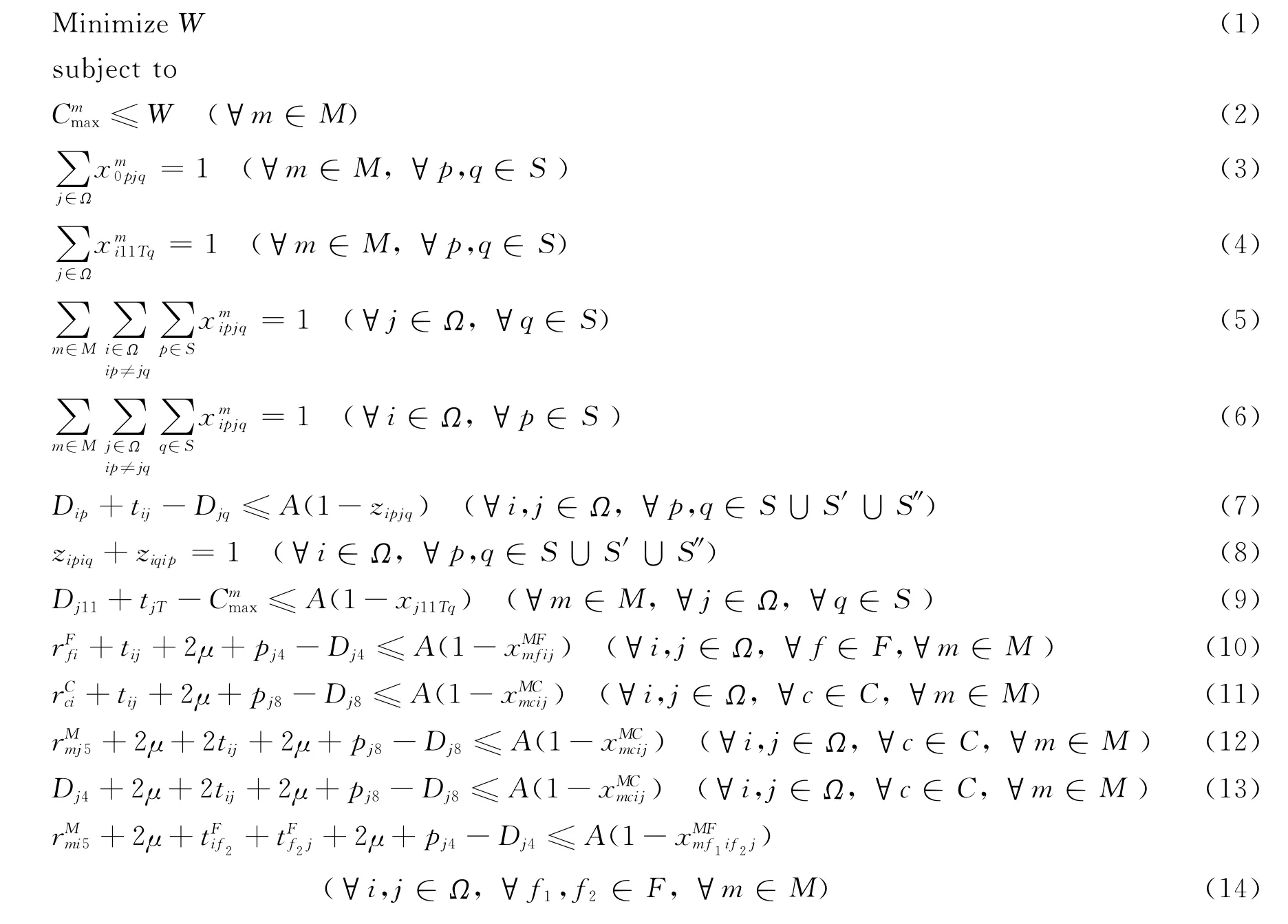
1.3 模型的分析


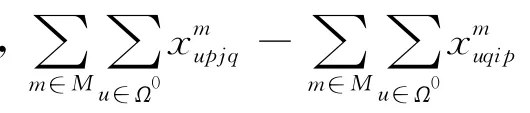
上述模型包括大量的整数变量,即使一台吊机,使用CPLEX软件尝试解决8个工件的例子,预处理时间已经超过40 min.鉴于很难在合理的时间内对这个实际问题求得最优调度,因此需要进一步探究问题的性质并提出近似算法.
2 一种整合的方法
这种整合的方法可以将罩式退火过程划分为8个阶段,再将这8个阶段过程整合为3层.
第一层 由于前三个阶段不需要作任何决策,因此这一层包括3个阶段.在这一层,装载一个板卷垛、内罩和自然充气的过程(阶段0,1和2)可以看做一道工序.
第二层 这一层从装载加热罩到卸载冷却罩(阶段3,4,5,6,7,8和9).一方面,需要将数量有限的工具(加热罩和冷却罩)分配给工件;另一方面,在避免吊机碰撞的基础上调度这些工具.
第三层 把最后两阶段连续地进行看做一道工序(阶段10和11).吊机将内罩卸载到炉台旁边后再将工件卸载到卸载站.
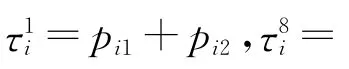
3 两阶段启发式算法及绝对性能分析
3.1 两阶段启发式算法
这部分提出一个两阶段启发式算法H,包括分配工具和调度吊机两方面.第一阶段包括吊机的分配和工具的分配.一方面,将工作区域分成|M|个互不重叠的子区域,使每个吊机分配到各自的操作区域;另一方面,将每台工具分配到已划分好的子区域.也就是说,问题可以看做|M|个互不相关的单吊机调度问题.
3.1.1 吊机分配策略
从左至右,将子区域编号{1,2,…,R}.令L表示在每个子区域内工件的个数,如图1所示,R=10,L=3.令ak表示分配给吊机k的最小基本子区域的编号k=1,2,…,|M|.因此,{ak,ak+1,…,ak+1-1}即为分配给吊机k的子区域集合.根据子区域的编号方式,所有的子区域相互独立,独一无二地分配吊机.显然,有
{a1,a1+1,…,a2-1,a2,a2+1,…,
a3-1,…,am,am+1,…,R}= {1,2,…,R}.
令t(i,j)表示位于从基本区域i到j的子区域中工件总装载时间和卸载时间和,i≤j.f(k,sk)表示由吊机k操作工件的最小总完工时间,k=1,2,…,|M|,其中,ak=sk.也就是分配给每个吊机k,k+1,…,|M|的子区域集合分别为{sk,sk+1,…,ak+1-1},{ak+1,ak+1+1,…,ak+2-1},…,{am,am+1,…,R}.事实上,每台吊机每次只能对{1,2,…,R}集合中的一个基本子区域内的工件进行操作,同时覆盖这个基本子区域的位置.根据t(i,j)和f(k,sk)的定义,
如果k=1,那么f(1,s1)=t(s1,a2-1),其中,s1=1,2,…,R-m+1.
如果k=m,那么f(m,sm)=t(sm,R),其中,sm=m,m+1,…,R.
如果1<k<m,那么f(k,sk)=t(sk,ak+1-1),其中,sk=k,k+1,…,R-m+k.
随着操作区域被划分成|M|个互不重叠的子区域,吊机分配的策略可以由下式确定:
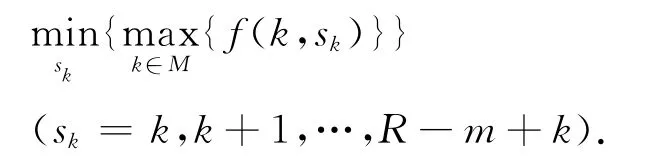
由于所有的工件事先放在装载站中,因此计算t(sk,ak+1-1)等价于为|M|个吊机分别选择每个子区域的工件.
3.1.2 工具分配策略
将在已划分好的每个子区域内给出工具的分配策略.以加热罩分配为例,冷却罩的分配与加热罩相同.本文中用[x]表示不小于x的最小整数.令Sk表示由吊机操作的子区域,其中,k=1,2,…,|M|.ΩSk表示在S k中的工件集合.不失一般性,假设Sk中分配到的加热罩数|FSk|满足1≤|FSk|≤|F|.
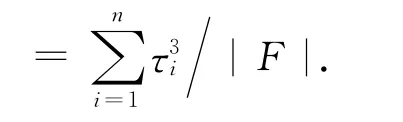
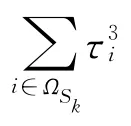
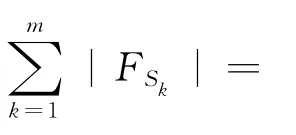
3.1.3 调度阶段
基于工具的分配,调度阶段尽可能减少吊机和工具的空闲或者等待时间.每个子区域内的单吊机调度描述如下:
第1步 优先于其他操作阶段装载所有的工件.
第2步 决定任意两个分享同一加热罩的工件加热顺序.
第3步 为了尽可能减少吊机空闲时间,计算工件某阶段最早需要吊机操作的时间(工件某阶段最早的完工时间减去吊机从当前位置到工件之间的移动时间).
3.2 启发式的绝对性能分析
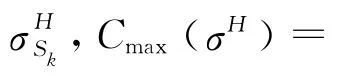
由于每台工具一次最多加工一个工件,可行的吊机调度不能小于在每个子区域内一个工件各阶段加工时间的总和.这提供了确定最优调度值的下界.另一方面,如果问题的可行解存在,那么依次加工完各工件的总时间提供了最优调度值的上界.因此,可以得到下面的结论:
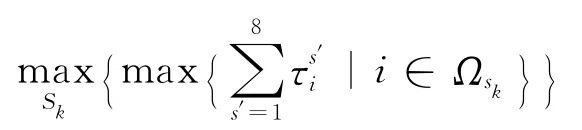
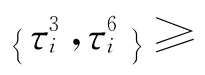
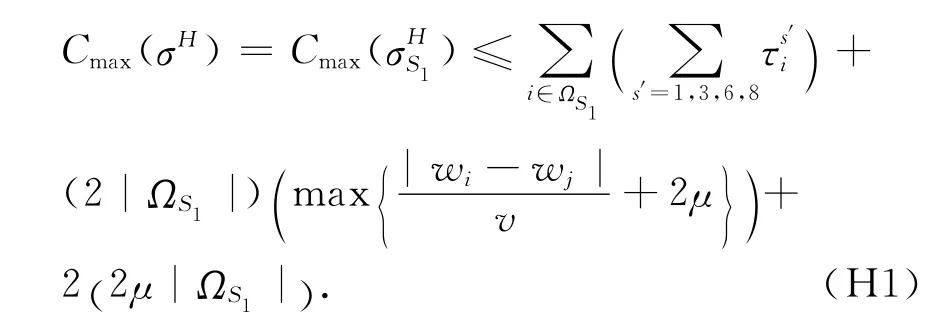
最后一项表示所有加热罩和冷却罩卸载到最后位置的时间.
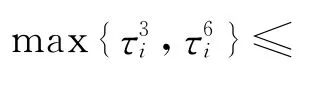
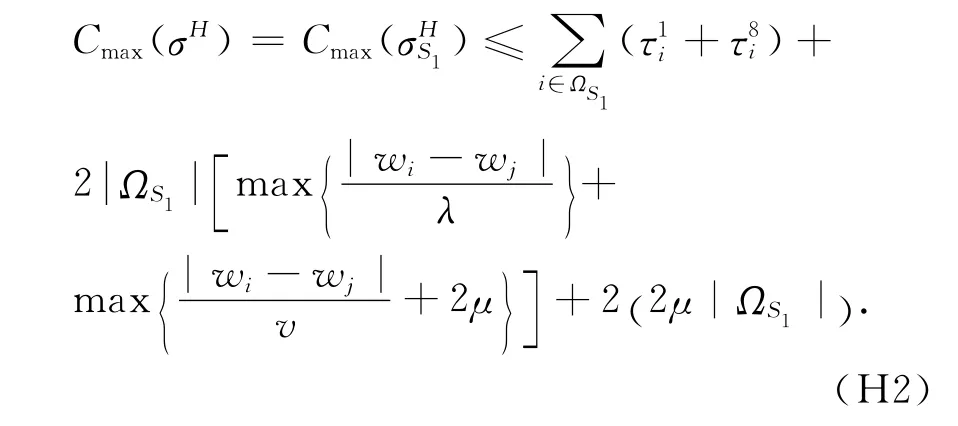
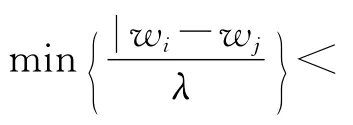
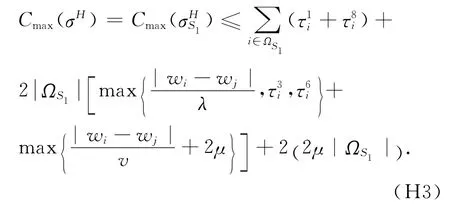
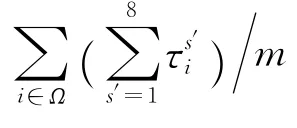

结合n=RL,可以得到下面的定理:
定理1 对任意一个由算法H产生的调度σH,它的绝对性能保证为
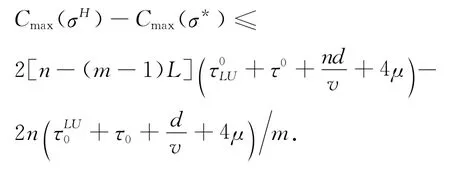
4 结 语
本文研究了罩式退火过程中的多吊机调度问题以最小化最大完工时间.这个被证明为强NP难的实际问题,本文给出了混合整数规划模型,并提出一种整合的方法以简化问题并保持问题的本质.在此基础上提出一个启发式算法并从绝对性能的角度分析了这个算法.
本文可以扩展为多方向的.如,对于加热罩(冷却罩)不同这样更一般的情况提出和分析算法.此外,基于理论分析的其他目标函数的该问题也是吸引我们进一步研究的方向.
[1] Liu J Y,Jiang Y,Zhou Z L.Cyclic scheduling of a single hoist in extended electroplating lines:a comprehensive integer programming solution[J].IIE Transactions,2002,34(10):905-914.
[2] Liu J Y,Jiang Y.An efficient optimal solution to the two-hoist no-wait cyclic scheduling problem[J].Operations Research,2005,53(2):313-327.
[3] Jiang Y,Liu J Y.Multihoist cyclic scheduling with fixed processing and transfer times[J].IEEE Transactions on Automation Science and Engineering,2007,4(3):435-450.
[4] Lee C Y,Lei L,Pinedo M.Current trends in deterministic scheduling[J]. Annals of Operations Research,1997,70(1):1-41.
[5] Hall N G,Kamoun H,Sriskandarjah C.Scheduling in robotic cells:complexity and steady state analysis[J].European Journal of Operational Research,1998(109):43-65.
[6] Mak R,Wong Y,Leung J M Y,et al.The hoist scheduling problem for no-wait production lines:a survey of research[R]∥Technical Report SEEM 2000—2005.2000.
[7] Crama Y,Kats V,Van de Klundert J,et al.Cyclic scheduling in robotic flowshops[J].Annals of Operations Research,2000,96:97-124.
[8] Liu J Y,Wan Y W,Wang L.Quay crane scheduling at container terminals to minimize the maximum relative tardiness of vessel departures[J]. Naval Research Logistics,2006(53):60-74.
[9] Zhu Y,Lim A.Crane scheduling with non-crossing constraints[J].Journal of the Operational Society,2006(57):1464-1471.
[10] Bish E K. A multiple-crane-constrained scheduling problem in a container terminal[J].European Journal of Operational Research,2003(14):83-107.
[11] Moccia L,Cordeau J F,Gaudioso M,et al.A branch-and cut algorithm for the quay crane scheduling problem in a container terminal[J].Naval Research Logistics,2006(53):45-59.
[12] Ngw C.Crane scheduling in container yards with intercrane interference[J].European Journal of Operational Research,2005,164(1):64-78.
[13] Moon S,Hrymak A N.Scheduling of the batch annealing process:deterministic case[J].Computers and Chemical Engineering,1999,23(9):1193-1208.
[14] Xie X,Tang L X.Crane Scheduling in Batch Annealing Process[C].Proceedings of the IEEE International Conference on Automation and Logistics,Qingdao,2008.
Multi-Crane Scheduling in Batch Annealing Process
XIEXie,LIYanping
(Key Laboratory of Manufacturing Industrial and Integrated Automation,Shenyang University,Shenyang 110044,China)
A multi-crane scheduling problem was addressed,which is motivated by batch annealing process(BAP)in the iron and steel factory.The objective is to minimize the last coil annealing completion time(makespan).A mixed-integer linear programming(MILP)model is formulated by considering both positions of bases and cranes.Afterwards,an aggregate approach is proposed to reduce problem difficulty but keep the essential features of practical problem.However,the aggregated problem is still proofed strongly NP-hard.A two-phase heuristic algorithm is proposed,which consists of assignment and scheduling.The assignment phase based on a dynamic programming is to assign each crane to its exclusive sub-region,followed by a resource assignment to each subregion.Scheduling phase adopts an earliest requirement performed stage first strategy.Finally,from an absolute performance point of view,the quality of the proposed heuristic is measured.
crane scheduling;batch annealing process;strongly NP-hard;heuristics;absolute performance analysis
TG 156.2
A
1008-9225(2012)01-0012-08
2011-11-10
国家自然科学基金资助项目(61104029);辽宁省教育厅基金资助项目(L2011207).
谢 谢(1981-),女,辽宁沈阳人,沈阳大学讲师,博士;李彦平(1958-),男,辽宁沈阳人,沈阳大学教授,博士.
刘乃义】
