运输与倒垛集成的多吊机调度问题
2014-03-25李彦平
谢 谢, 李彦平
(沈阳大学 装备制造综合自动化重点实验室, 辽宁 沈阳 110044)
本文研究了在钢铁企业钢卷仓库中出现的一个问题,如图1所示.一些成品或半成品板卷已经被存放在仓库中等待被客户或下道工序选择.根据实际存储的需求,每个板卷已经被放在了预先指定的按两层摆放的位置上.如果一个需求板卷在上层或无板卷阻碍的下层,它可以被直接运输到指定位置;如果一个需求板卷在下层并且由上层的一个或两个板卷阻碍,直到阻碍板卷需要被运到另外的位置后,它才能被运输到指定位置.为了便于描述问题,前一种情况称为运输操作,后一种情况称为倒垛操作.这两种操作都由贵重的设备即上方移动的许多吊机实施.目的就是确定一个联合运输和倒垛操作的多吊机调度,使得所有的需求板卷尽快被运输到指定位置,同时确定每个阻碍板卷需要倒垛的位置.这个问题经常出现于存储成品或半成品板卷的钢铁企业仓库中,如热轧后库、热镀锌原料库、酸洗原料库和酸轧后库.另外,在集装箱终端的垛场和造船厂原料库也存在该问题.然而,现有的文献几乎没有研究该问题的.

图1 钢铁企业生产物流图Fig.1 Production and logistics flow chart in iron and steel enterprises
该问题通常如下描述. 给定一些位于仓库某区中的候选板卷.一旦收到来自客户和生产线的需求板卷列表,这些板卷由处于上方的覆盖该区的双向跨上的一些吊机实施操作,如图2所示.为了方便描述,定义一个板卷为一个工件.每个吊机从一个地方移动到另一个地方意味着它的提起设备(吊钩)随着吊机不仅沿着平行的跨移动,而且在跨之间移动,两方向的移动是同时进行的.本文中,将吊钩看作吊机.本文研究在避免吊机碰撞的约束下,决策联合运输操作和倒垛操作以最小化最后一个需求板卷被运输到指定位置的完成时间(makespan).

图2 钢卷仓库一个区域的板卷存储Fig. 2 Coil storage in a block of steel coil warehouse
有关吊机调度的文献通常仅考虑吊机的一种操作[如集装箱码头的岸吊(QC)或场吊(YC)调度和电镀生产线中的吊机(HS)调度],并没有考虑多吊机的运输与倒垛的集成操作.一些研究致力于和其他设备的集成研究以调度吊机[1-5]. 一些研究仅致力于研究两台或多吊机调度问题.Lei和Wang[6]提出了两台吊机周期调度的一个算法.他们通过划分两个区域将每台吊机分配给专门的区域进行研究,然而连续的相邻两区不能保证吊机之间不碰撞.Armstrong等[7]提出了一个贪婪搜索算法以确定吊机的最小数目.Liu和Jiang[8]研究了工件具有固定加工时间和移动时间的两台吊机调度问题,提出了一个多项式时间最优算法.Zhou和Liu[9]提出了解决具有重叠区域的两台吊机周期调度问题的一个启发式算法.对于多吊机调度问题,Varnier 等[10]使用约束逻辑规划的方法确定当给定吊机分配时的最优调度.Jiang和Liu[11]提出了具有固定加工时间和移动时间的多吊机问题的多项式时间最优算法.
然而,之前提及的这些问题或者是本文考虑问题的特殊情况,或者与本文研究的问题不同.研究目的就是减少存储时间,但并没有同时考虑到吊机的运输倒垛集成调度.尽管有一些研究主要考虑倒垛,但在这些问题中,工件按照每个工件上仅有一个工件阻碍的方式堆放,比起上述研究的问题简单得多.此外,大部分的研究主要考虑单吊机调度,多吊机调度问题研究得相对较少.大多数研究主要考虑智能计算以获得近优解,很少有研究对吊机调度问题进行理论分析.因此,大部分文献不能直接应用于解决上述问题.该问题有如下两个特点:吊机操作集成了运输和倒垛两道工序;协调调度吊机,避免相邻吊机之间碰撞.这需要在考虑问题特点和约束的基础上提出新的算法.
1 问题的符号和分析



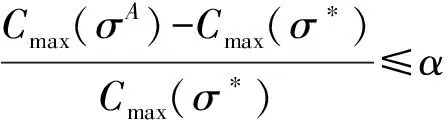
2 问题模型
为了更清晰地描述上面描述的问题,在这部分中,提出了一个混合整线性规划模型(MILP).
2.1 问题参数
输入数据如下.

μ对应于吊机上提和下放一个工件的时间.
v1,v2和λ1,λ2对应于吊机带着工件和不带工件沿着两个方向移动的速度 ,为了表达方便,本文中,令λ=min{λ1,λ2},v=min{v1,v2}.不失一般性,假设λ≥v≥1.
A是一个很大的正整数.
决策变量如下:
xmij=1,如果工件Ji被吊机m倒到工件Jj的位置(Ji,Jj∈Ω0,m∈M);否则,xmij=0.


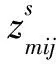
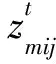
zij=1,如果工件Jj的一道工序(倒垛或运输)在工件Ji的一道工序(倒垛或运输)结束后开始(Ji,Jj∈Ω0);否则,zij=0.
smi,吊机m(m∈M)从工件Ji的位置移动的开始时间(Ji∈Ω或Ji∈Ω0).根据吊机的移动可知,如果吊机带着工件开始移动,这是装载移动的开始时间;否则,是空移动的开始时间.
emi,吊机m(m∈M)将工件Ji(Ji∈Ω0)倒垛后的结束时间.
Cmax,最后一个工件被运到指定位置的完成时间.
2.2 数学模型
问题的数学模型表示如下:
minCmax=max{Ci|Ji∈Ω}.
(1)
s.t.
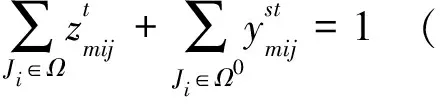
(2)

(3)
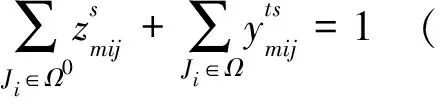
(4)

(5)

(6)
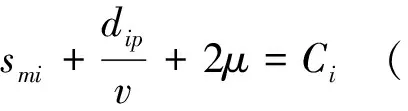
(7)
(∀Ji,Jj∈Ω0,∀m∈M);
(8)
(∀Ji∈Ω0,Jj∈Ω,∀m∈M);
(9)
(∀Ji∈Ω,Jj∈Ω0,∀m∈M);
(10)
(∀Ji,Jj∈Ω0,∀m∈M);
(11)
(∀Ji,Jj∈Ω,∀m∈M);
(12)
(∀Ji,Jj∈Ω0,∀m1,m2∈M);
(13)
(∀Ji,Jj∈Ω0,∀m1,m2∈M);
(14)
(∀Ji,Jj∈Ω0,∀m1,m2∈M);
(15)
(∀Ji,Jj∈Ω0,∀m1,m2∈M);
(16)
(∀Ji,Jj∈Ω0,∀m1,m2∈M);
(17)
(∀Ji,Jj∈Ω0,∀m1,m2∈M);
(18)
(∀Ji,Jj∈Ω0,∀m1,m2∈M);
(19)
(∀Ji,Jj∈Ω0,∀m1,m2∈M);
(20)
(∀Ji,Jj∈Ω0,∀m1,m2∈M);
(21)
(∀Ji,Jj∈Ω0,∀m1,m2∈M);
(22)
(∀Ji,Jj∈Ω0,∀m1,m2∈M);
(23)
(∀Ji,Jj∈Ω0,∀m1,m2∈M);
(24)
xmij∈{0, 1} (∀Ji,Jj∈Ω0,∀m∈M);
(25)

(26)

(27)

(28)
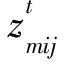
(29)
zij∈{0, 1} (∀Ji,Jj∈Ω0,∀m∈M).
(30)

由于文献[12]中研究的单吊机调度问题已经证明为强NP难的,因此,本文考虑的多吊机调度问题也是强NP难问题.这使得最优算法不能解决实际中的大规模问题,启发式算法能够有效地解决上述问题.在下面的部分中,提出了问题的一些最优性质,这些性质将应用在后面的启发式算法及其性能分析中.
3 启发式算法及其最坏性能分析
3.1 启发式算法



第3步 吊机的操作原则:一旦吊机空闲,如果存在没有被阻碍的需求工件,则吊机对该工件进行运输操作;否则,吊机进行倒垛操作.
第3.1步 对于运输操作,如果存在多需求工件,吊机选择权最大的工件进行操作.
第3.2步 对于倒垛操作,吊机选择距离当前位置最近的阻碍工件,将其倒到最近的下层空位置,如果不存在这样的空位,则选择上层中不阻碍需求板卷的位置;否则,吊机选择距离当前位置次最近的阻碍工件进行操作.如果一个需求工件被运输到指定位置,则从列表中删除.
第4步 当两台或多台吊机同时可利用时,根据第5步分配吊机.根据第3步执行每台吊机的操作.一旦发生吊机冲突,转第6步.
第5步 检验吊机操作的可行性.
第5.1步 检验分配的吊机号是否在可行范围内,如果可行,则构建一个吊机启发式;否则,转第6步.
第5.2步 为避免吊机碰撞,分别检验在相邻两行或同一行中的各种可能的情况.如果可行,则构建一个吊机启发式;否则,转第6步.
第6步 避免吊机碰撞的原则:
第6.1步 交换彼此的操作;
第6.2步 一台吊机等待直到另一台吊机完成当前的操作.
性质1 启发式的计算复杂度为o(n2N2×|M|2).
证明 在第2步中,需要时间o(|M|×NlogN).第3步和第4步中,吊机运行时间分别为o(nN)和o(nN|M|).第5步中,检验吊机操作的可行性时间为o(nN|M|).因此,算法的复杂度为o(n2N2|M|2).
3.2 最坏性能分析
为了分析算法的最坏性能比,根据三种不同的情况得到了三个下界.由于几个下界之间互相补充,没有一个能代替另一个,因此,进一步采用复合下界的策略,使得得到的问题的下界可以更接近最优值.基于这个界,分析了问题启发式的最坏性能.
自然的,可以把多吊机对工件的操作看作平行机.一个下界为
当所有的需求工件位于上层或无阻碍板卷压迫的下层时,这个界的值更紧.等式右边第一项的值需要决策,第二项的值为常数.注意,这个下界忽略了吊机的空移动时间.因此,不采用它作为问题的下界.
从吊机运输操作的角度看,一个可行调度的最大完工时间不能小于运输一个工件的时间.因此,得到的下界为
从吊机倒垛操作的角度看,一个可行调度的最大完工时间不能小于一个工件在|R|-|M|+1相邻行内由一台吊机进行倒垛操作的时间.显然,得到的另一个下界为
由上面的讨论可以直接得到以下结论.
令启发式算法得到的调度为σH.
性质2 问题的下界LB可由下面两个下界获得:LB=max{LB2,LB3}.
定理由启发式得到调度σH的最坏性能比为

证明 不失一般性,考虑一种最差的情况,即一台吊机m∈M对所有需求工件在|R|-|M|+1相邻行中进行操作.显然,在这种情况下,不需要考虑吊机间的彼此碰撞.如果没有阻碍工件,问题可以在多项式时间内求得最优解.因此,一个可行调度的最大完工时间或许依赖于阻碍工件:阻碍工件的个数越少,可以更容易地得到一个调度.根据阻碍工件的个数,算法的最坏性能可以根据阻碍工件的个数从下面3种情况中得到.
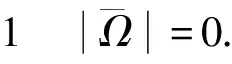
在这种情况下,算法可以得到最优调度,有Cmax(σH)=Cmax(σ*).

在这种情况下,可以为阻碍工件提供足够的倒垛位置而不会使需求工件再次被阻碍.根据第3步,在运输所有需求板卷之前,首先将所有阻碍板卷倒垛.调度σH的目标函数值不能超过需要倒垛的所有阻碍板卷的最长时间(两项的和)与需要运输的所有需求板卷的最短时间(后三项的和).
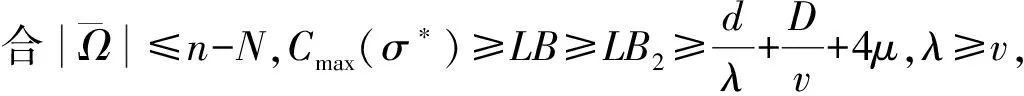
(a)

(b)

在这种情况下,由于阻碍工件没有足够的倒垛位置,因此,阻碍工件或许被倒到已经运走的需求工件的位置.也就是,一些需求工件被运输得更早.为了尽可能地减少倒垛时间,吊机或许将对工件进行倒垛和运输操作.因此,最大完工时间Cmax(σH)总是满足下式:
式中,右边第一项为吊机从初始位置到一个工件的最大空移动时间,后3项的和为最大的倒垛与运输时间的和.


因此,最坏性能为max{(a),(b),(c),(d)}.
4 结 语
本文不同于之前的相关文献,对这个实际问题通过理论分析的方式进行了研究.问题被描述为一个混合整规划模型,由于问题是强NP难的,提出了一个有效的启发式算法,这个算法的性能与问题的参数有关,这个算法为改进吊机的运行效率、及时地为下道工序运输工件、提高钢铁企业的产能提供了一个依据.
上述问题适用于在钢铁企业仓库中解决避免吊机碰撞的约束下,运输需求板卷多吊机协调调度问题.除了钢卷仓库中的问题可以应用,这个研究在考虑具体的实施细节时也可以扩展到类似的板坯仓库和集装箱码头的倒垛、重倒垛问题.
协调调度吊机与其他物流和运输设备,如钢铁企业的台车和卡车、集装箱码头的船只和场吊,都是将来进一步研究的问题.
参考文献:
[ 1 ]Guan Y, Cheung R K. The Berth Allocation Problem: Models and Solution Methods[J]. OR Spectrum, 2004,26(1):75-92.
[ 2 ]Imai A, Sun X, Nishimura E, et al. Berth Allocation in a Container Port: Using a Continuous Location Space Approach[J]. Transportation Research Part B: Methodological, 2005,39(3):199-221.
[ 3 ]Park Y M, Kim K H. A Scheduling Method for Berth and Quay Cranes[J]. OR Spectrum, 2003,25(1):1-23.
[ 4 ]Kim K H, Moon K C. Berth Scheduling by Simulated Annealing[J]. Transportation Research Part B: Methodological, 2003,37(6):541-560.
[ 5 ]Neumann K, Zimmermann J. Procedures for Resource Leveling and Net Present Value Problems in Project Scheduling with General Temporal and Resource Constraints[J]. European Journal of Operational Research, 2000,127(2):425-443.
[ 6 ]Lei L, Wang T J. The Minimum Common-Cycle Algorithm for Cyclic Scheduling of Two Material Handling Hoists with Time Window Constraints[J]. Management Science, 1991,37(12):1629-1639.
[ 7 ]Armstrong R, Gu S, Lei L. A Greedy Algorithm to Determine the Number of Transporters in a Cyclic Electroplating Process[J]. IIE Transactions, 1996,28(5):347-355.
[ 8 ]Liu J Y, Jiang Y. An Efficient Optimal Solution to the Two-hoist No-wait Cyclic Scheduling Problem[J]. Operations Research, 2005,53(2):313-327.
[ 9 ]Zhou Z L, Liu J Y. A Heuristic Algorithm for the Two-hoist Cyclic Scheduling Problem with Overlapping Hoist Coverage Ranges[J]. IIE Transactions, 2008,40(8):782-794.
[10]Varnier C, Bachelu A, Baptiste P. Resolution of the Cyclic Multi-hoists Scheduling Problem with Overlapping Partitions[J]. INFOR, 1997,35(4):309-324.
[11]Jiang Y, Liu J Y. Multihoist Cyclic Scheduling with Fixed Processing and Transfer Times[J]. IEEE Transactions on Automation Science and Engineering, 2007,4(3):435-450.
[12]谢谢,李彦平. 钢卷仓库中的吊机调度问题[J]. 沈阳大学学报:自然科学版, 2014,26(2):159-165.
(Xie Xie, Li Yanping. Crane Scheduling in Warehouse of Coil[J]. Journal of Shenyang University: Natural Science, 2014,26(2):159-165.)
