基于激励策略自报电量的电价算法研究

王 丹，李彦平

（沈阳大学 装备制造综合自动化重点实验室，辽宁 沈阳 110044）

基于激励策略自报电量的电价算法研究

王 丹，李彦平

（沈阳大学 装备制造综合自动化重点实验室，辽宁 沈阳 110044）

研究了用户自报用电量的激励电价的建模问题，并设计了相应的电价算法.该模型的主要思想是，让用户自己申报每月的计划用电数额，实际用电超额或是没达到自报额，将给予惩罚性质的电价.运用对策论中的激励Stackelberg策略对模型中的单位电价进行线性激励.此电价模型鼓励用户根据自己的实际需要自报合适的用电量，从长远效益来看，起到了节约资源、满足需求的作用.最后，利用MATLAB对所制订的激励策略进行了数值仿真，仿真结果说明所得方法的有效性和结果的实用性.

电力市场；电价策略；Stackelberg策略；效用函数

电力市场是电力的买方和卖方相互作用以决定其电价和电量的过程.更具体地讲，电力市场是采用经济手段，本着公平竞争、自愿互利的原则，对电力系统中发电、输电、配电、用户等各成员组织协调运行的管理机制和执行系统的总和［1］.价格是商品价值的货币表现，电能也是一种商品，电价是电能价值的货币表现.另外，商品价格由供求关系决定.在竞争电力市场下，电价由电力市场中的供电量和用电量决定.在供电量和用电量平衡时达到均衡价格［2］.

电力企业根据电力需求双方的具体情况，合理确定电价策略，对电力企业的发展具有举足轻重的作用，同时也影响电力企业与客户之间的合作以及能否有效地使用电力和节约电力［3－4］.如何制定合理的电价，国内外学者已经进行了很多的研究工作.目前在我国已经实施和可能实施的电价机制主要有固定电价、阶梯电价、分时电价和实时电价4种［5］.固定电价是价格不随时间波动的电费收取方式，这种电价难以反映电力的供需关系及节能减排的需要.阶梯电价［6－7］是把每户平均用电量设置为若干个阶梯，按照阶梯式累进电价计收电费，这种电价可以通过价格杠杆来抑制用户的需求，从而达到节能减排的目的.然而，从刺激消费、拉动内需的角度看，这种电价抑制了居民的消费意愿，难以起到拉动内需的作用.分时电价［8］是将每个交易日分成不同的时段，根据每个时段的用电状况确定该时段的电价，峰谷电价［9－10］作为分时电价的初级形式，在我国的电力工业中已被采用.不过，目前由于我国的峰谷电价在实施中还存在实用行业窄、峰谷电价差距不合理等诸多因素，影响了峰谷电价的实施效果.实时电价［11］是随时间变化的电价，这是电力市场最理想的电价，但这种电价却从技术角度上缺乏可操作性.

鉴于目前电价机制的局限性，本文以一定数额的电量为基础，建立一种鼓励用户自报电量的电价模型.该模型允许用户自己申报每月的用电数额，超额或是没达到自报额的部分，将赋予惩罚性质的电价.建立模型有两个目的，一是要求完成电厂的生产计划，并希望尽量不要过多地消耗用电；二是希望能及时了解消费者真实的消费水平并预见可能的超额用电情况，并以此来调整电厂的生产计划.

在对策论模型［12］中，至少存在两个局中人分别控制其输入以使系统状态达到各自所要求的输出.因此，对策论［13］提供了一个分析非合作网络［14］动态特性的体系结构.激励Stackelberg策略是由Ho Y C等人引入到对策论中的［15］.这里的激励策略由两部分组成，其一是正常价格，其二是惩罚价格，后者依赖于供电量的变化.

1 自报电量算法模型的建立

考虑一个电力网络系统J，令Cj为系统j的有限容量，j∈J.系统S中的用户以p＝（p1，p2，...，ps）来使用电量.对于每个用户s，其最大效用模型如下：

式中，U s（p s）为用户s的效用函数，在ps≥0的范围内，它是连续可导的严格凹增函数；λs是用户s支付的单位电价.

如果电力公司在用户s的单位用电量下的收益为λs，则该电力网络系统的最大收益模型可表示为

模型（2）满足Hy＝p，Ay≤C（p，y）≥0，其中，H和A为0－1矩阵，y为流量模式.

由Kelly F的研究成果［16］可知，存在一个价控向量λ＝（λ1，λ2，…，λs），使得模型（2）的解向量为由模型（1）对于任意s∈S的唯一解p s构成的向量p＝（p1，p2，…，p S）.

由式（1）和式（2）可以看出，它们中有符号正好相反的部分λsp s，因此可以把模型（2）看做模型（1）的逆问题.

下面建立一种带有激励性质的电价模型：

式中，Fs为电费，为用户自报的用电量，ps为用户实际的用电量，β＞α＞γ为电费单价.上面的激励电价策略可作如下解释：如果用户自报用电量偏低，则超额用电量部分（ps－）将以较高的用电单价β来计费；而当用户的自报用电量较高时，其未达到部分（ps－）只能以较低的用电单价γ来扣除.其结果均不如自报准确额ps＝时的花费小.当然，不论自报电量为何，用电费用永远是实际用电量的递增函数，因此，这一激励策略总是鼓励用户少用电.从长远效益来看，起到了节约资源的作用.因为有这样的激励策略，用户会努力调整自己的用电量，尽量准确地申报用电量，这样电力公司就可以了解真实的用电潜力并预见可能的超额情况，以便及时调整定额，取得全局最优，从而起到有效的宏观调控作用.

在此，将对策论中的Stackelberg策略引入该模型中，对β和γ进行激励.在这个策略中，电力公司是主方，而各用户是满足Nash平衡点的从方，且允许用户和电力公司的控制者随意改变电量ps，其中，s＝1，2，…，S.如果主方要求用户达到系统所规定的电量，则它在对策中必处于主导地位，这正可由下述Stackelberg策略中体现出来：

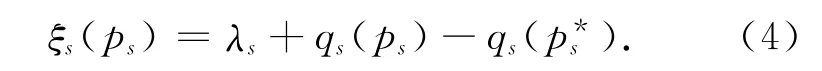
式中，ξs（ps）为激励策略函数，qs（ps）为p s的待确定的任意函数，p＊s为电力网络中电量要求的期望点.

2 线性激励Stackelberg策略的设计

在这里分别对β和γ采用线性激励Stackelberg策略，改造如下策略：

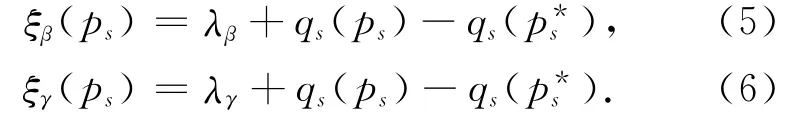
将qs（p s）选为线性函数，即

式中，k为惩罚价格，由主方来确定.

以线性函数（7）作为迫使用户达到点p＊s的激励Stackelberg策略.满足Stackelberg激励策略的条件为［17］

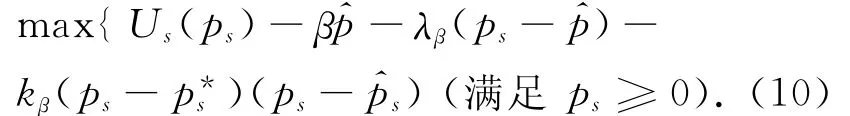
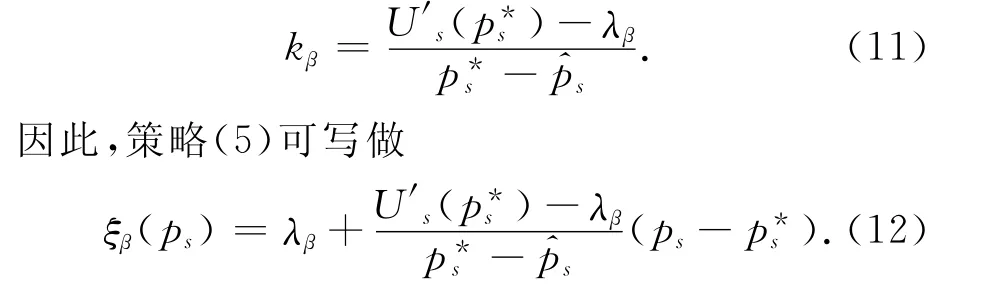
显然，式（8）可由式（12）的表达式推出.由方程（9）应得到下列不等式：

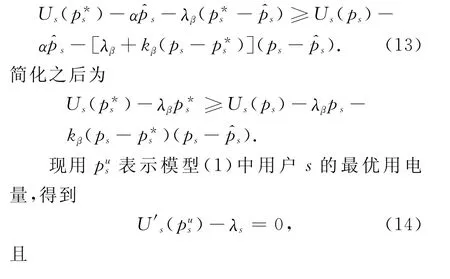
3 数值例子及仿真结果

在这里引入Kelly F的效用函数形式［16］，令用户s的效用函数为U s（p s）＝μlgps，当μ＝200且α＝0.7时，根据约束条件式（23）和式（24），分别令λβ＝0.8，λγ＝0.3，可以得到

由式（11）和式（21）可以分别得到在点＝320时，kβ＝0.025 8，kγ＝0.050 8.图1给出了在自报电量＾p＝300时用户的效用函数曲线.从图1可见，当用户消费的电量等于自报电量时，用户的效用函数最大.

图1 用户的效用函数曲线Fig.1 Curves of the functions

图2为斜率分别是kβ＝0.025 8，kγ＝0.050 8的分段线性激励策略曲线.当用户的用电量超过自报额时，用户的单位电价以斜率kβ＝0.025 8线性增长.当用户的用电量没达到自报额时，其未达到部分（ps－）只能以较低的用电单价ξγ（p s）来扣除，其中，ξγ（ps）以斜率kγ＝0.050 8递减.

图2 分段线性激励策略曲线Fig.2 Curves of subsection linear incentive strategy

将仿真数据代入式（3）中，得到

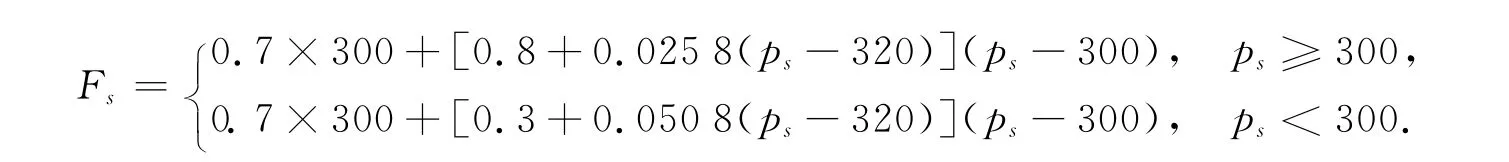
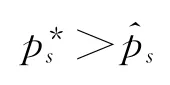
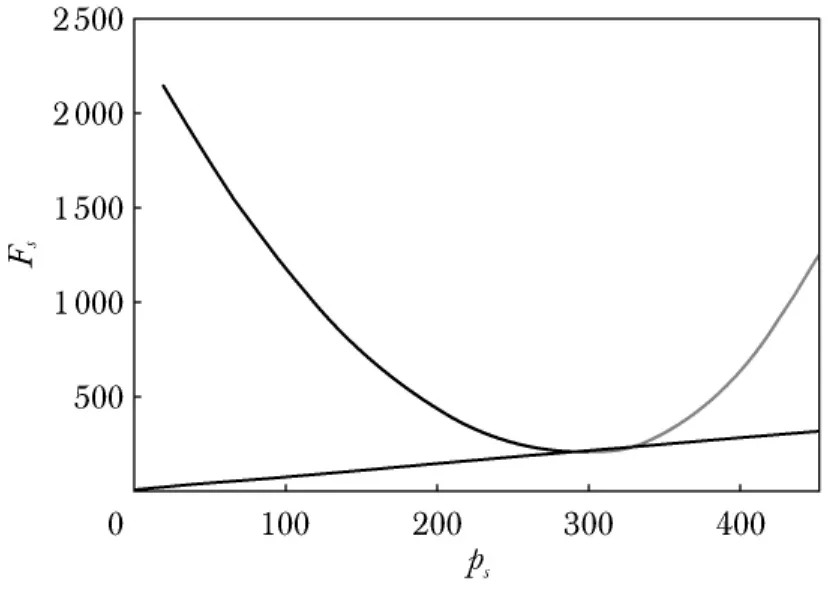
图3 激励策略下的价格仿真图示Fig.3 Price illustration of simulation with incentive strategy

4 结 语

首先建立了一种用户自报电量算法数学模型，在该模型中由用户自己申报每月的用电数额，超额或未达到自报额的部分，将赋予惩罚性质的电价.其次应用对策论中的激励Stackelberg策略对此算法数学模型中的电费单价进行激励性质的惩罚.这一激励策略总是鼓励用户根据自己的实际需要自报合适的用电量.从长远效益来看，起到了节约资源、满足需求、促进用户合理用电的作用.因为有这样的激励策略，用户会努力调整自己的用电量，尽量准确地申报用电量.如果此策略能够实施，那么电力公司可以了解消费者真实的用电潜力并预见可能的超额情况，并及时调整电厂的生产计划，达到供需平衡，从而起到有效的宏观调控作用.

［1］ 汤振飞，唐国庆，于尔铿，等.电力市场输电定价［J］.中国电机工程学报，2001，21（10）：91－95.

［2］ 高海波.电力市场中的电价及其本质探析［J］.电网技术，1998，22（6）：73－75.

［3］ 刘敏，张岚，李俊松.运用电价策略促进电力营销［J］.云南电业，2004（4）：30－31.

［4］ Gross A.The Global Market for Power Tools［J］.Business Economics，2006，41（3）：66－73.

［5］ 殷树刚，苗文静，拜克明.准实时电价策略探析［J］.电力需求侧管理，2011，13（1）：20－23.

［6］ 朱成章.阶梯电价是我国电价改革的阶梯［J］.中外能源，2011，16（3）：7－12.

［7］ 宋艺航.我国居民生活用电阶梯电价设计优化模型［D］.北京：华北电力大学（北京），2011.

［8］ 王庆利，王丹，井元伟，等.激励Stackelberg策略下的电价算法［J］.东北大学学报：自然科学版，2006，27（1）：1－4.

［9］ 唐捷，胡秀珍，任震，等.峰谷分时电价定价模型研究［J］.电力需求侧管理，2007，9（3）：12－15.

［10］ 胡福年，汤玉东，邹云.需求侧实行峰谷分时电价策略的影响分析［J］.电工技术学报，2007，22（4）：168－174.

［11］ 田建伟，胡兆光，周景宏，等.电网—用户互操作性对负荷曲线影响的定量模拟［J］.电力系统自动化，2011，35（13）：44－48.

［12］ Fudenberg D，Tirole J.Game Theory［M］.Cambridge：MIT Press，1992：17－25.

［13］ Myerson R B.Game theory：analysis of conflict［M ］.Cambridge：Harvard University Press，1991：97－101.

［14］ Bertsekas D，Gallager R.Data networks［M］.2nd ed.Englewood Cliffs：Prentice－Hall，1992：86－88.

［15］ Ho Y C，Luh P B，Olsder G J.A control－theoretic view on incentive［J］.Automatica，1982，18（2）：167－179.

［16］ Kelly F.Charging and rate control for elastic traffic［J］.European Transactions on Telecommunications，1997，8（1）：33－37.

［17］ Basar T，Olsder G J.Dynamic noncooperative game theory［M］.2nd ed.Philadelphia：SIAM，1998：7－201.

Power Pricing Algorithm of Consumption Report Model based on Incentive Strategy

WANGDan，LIYanping
（Key Laboratory of Manufacturing Industrial Integrated Automation，Shenyang University，Shenyang 110004，China）

The modeling of incentive electricity price in the model of the user self－reported consumption was studied and the algorithm of electricity price was designed.The main idea of the model is that users apply the amount of electricity，the part of excess or leavings will be appropriate punished.By using the incentive Stackelberg strategy in the game theory，a linear strategy to unit power price was established.Depending on the model，users are always encouraged to declare the amount of electricity demand according to practical demand.In the long term，resource can be saved and demand can be satisfied.Some numerical simulations were carried out for the linear strategy via MATLAB，thus illustrating the effectiveness and practicability of the proposed algorithm.

electric power market；electricity price method；Stackelberg strategy；surplus value

F 202

A

1008－9225（2012）01－0020－05

2011－11－03

国家自然科学基金资助项目（61104029）.

王 丹（1979－），女，辽宁沈阳人，沈阳大学讲师，博士.

刘乃义】