基于变位储油罐罐容表标定方法研究
2012-01-04岳晓宁安哲成于广灜张玲玲
岳晓宁,安哲成,于广灜,张玲玲
(1.沈阳大学 理学院,辽宁 沈阳 110044;
2.大连理工大学 信息与通信工程学院,辽宁 大连 116024;
3.大连理工大学 能源与动力学院,辽宁 大连 116024)
基于变位储油罐罐容表标定方法研究
岳晓宁1,安哲成2,于广灜3,张玲玲1
(1.沈阳大学 理学院,辽宁 沈阳 110044;
2.大连理工大学 信息与通信工程学院,辽宁 大连 116024;
3.大连理工大学 能源与动力学院,辽宁 大连 116024)
针对卧式储油罐发生纵向倾斜时罐容表标定的问题,从“理想容器”出发,给出了无变位与变位情况下,液面平面和规则几何体围成的油品体积与显示液面高度的关系的数值积分公式,并以此作为标定系统估计实际情况下的油品容积.分析了这种理想容器标定法的误差来源,并在此基础上引入了等效液面高度标定法,即将变位后的液面测量的高度折算成无变位时液面的等效高度,然后通过由实测数据得出的无变位油罐罐容表来制定标定系.同时对以上两种基本变位罐容标定体系的误差来源进行了分析.
标定;罐容;容量计量;数值计算;误差分析
许多储油罐在使用一段时间后,由于地基变形等原因,罐体位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表不够准确,所以需要定期对罐容表进行重新标定.很多学者对罐容表标定问题进行了研究.文献[1-2]介绍了体积与油品液面高度的函数关系,并通过测量油罐实际参数,使该函数具体化.文献[3]讨论了影响油罐标定与计量的因素等.
罐容表的重新标定问题即是找出变位后测量高度与实际油量的关系.本文使用数学建模方法分析了油罐变位角与储油量和油位高度之间的关系,通过建立对应的数学模型解决储油罐的变位识别与罐容表标定的问题.
1 理想容器标定法
1.1 理想容器标定法的模型描述
为分析油罐内油品的体积问题,首先提出“理想容器”这一概念.“理想容器”是指罐体表面为曲面或平面、无凹凸,形状规则,罐体内部体积可以全部用来盛装油品,油品液面为平面,罐内液面以下体积全部被油品充满,液面以上无油品的一种理想状态下的油罐模型.理想容器内油品的体积即为油品液面和液面以下罐体内表面所为空间几何体的体积.由此,易得

式中,VActual为油罐内油品的实际体积,VIdeal为用理想容器模型求得的油品体积,δ为两者的误差.
1.2 理想容器容积计算公式
椭圆形卧式平头储油罐如图1所示.

图1 椭圆形卧式平头油罐示意图Fig.1 Diagram of Horizontal flat oval tank
以油浮子杆与油罐下表面的连接点处为原点O,将过原点的和椭圆柱轴线平行的直线作为x轴.垂直于x轴的平面截得椭圆柱体的横截面如图2所示.
设其长半轴长度为a,短半轴长度为b.以过原点且垂直于x轴的平面所截得的椭圆的短轴所在直线为z轴,椭圆的长轴所在直线为y轴构建y Oz平面.
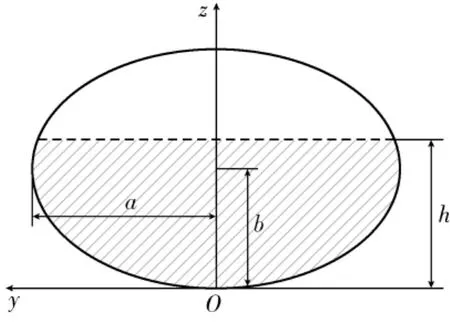
图2 油罐横截面示意图Fig.2 Diagram of tank cross-section
椭圆柱体的轴截面为图1所示的矩形,其宽为横截面椭圆的短轴长度2b.圆柱体最左端横坐标为x1,最右端横坐标为x2.
在此坐标系下,理想容器内油品的体积计算公式为

式中,S(h0,x)为位置为x处的液体的椭圆缺形横截面面积,h0为油浮子测得的液面高度.对于一个确定的位置,通过几何关系可以推导出椭圆缺面积S与椭圆截面液面高度h的关系
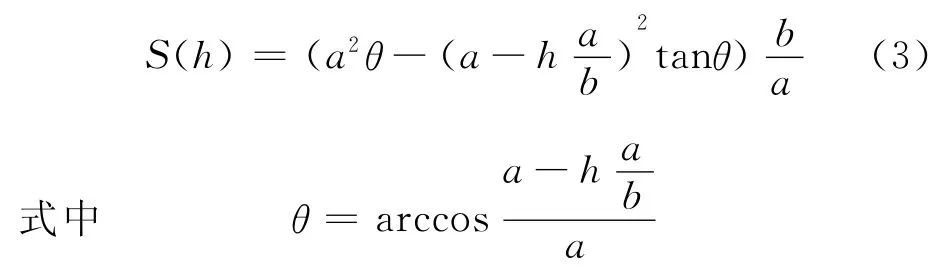
由此VIdeal即为位置x与对应液面高度h的函数,找到h与x的对应关系即可得到VIdeal的计算公式.
由于实验油罐不发生铅直方向的旋转,所以油浮子杆始终处于xOz平面内.当实验油罐轴线在x Oz平面内旋转一个α角的时候,相当于罐体在坐标系中保持不变[4],而油品液面绕某平行于y轴的直线旋转-α角.设此时油浮子测得的液面高度为h0,可以得到椭圆截面液面高度h的计算公式:

由于罐体倾斜,会出现油的液面低于油浮子最低位置或液面高于油浮子最高位置的情况,这是由于罐体倾斜造成的系统缺陷,此时的油品体积无法被测量.
将式(4)带入式(3),可以发现椭圆截面的液体面积仅仅是h0、α和x的函数,由于油罐纵向倾角α确定,h0与各处截面面积之间的关系即可确定.将该关系带入式(2),即可求得油罐内油的体积VIdeal的数值.
求解VIdeal时,对于式(2)中的积分式,虽然已经得知整体的解析表达式,但是如果直接对其进行符号积分,不仅涉及分段边界条件的讨论,而且运算极为烦琐.为了简化问题,使用数值积分方法对式(2)求解.数值积分式为


1.3 理想容器标定法的误差分析
标定体系中实际油品体积与理想体积有一定的差值,即标定体系中的误差量δ.它包含有理想容器系统本身的误差δsystem和偶然误差δAccidental,即

系统误差包含许多元素,如实际油罐内部不可能是完全标准的椭圆柱体,油罐内部存在输油管等因素使油罐内无法完全充满油品.同时在加油过程中,罐内温度的变化和罐内油压的变化都会影响到油量的标定[5].进行测量的油浮子在经过一段时间的使用后,也可能产生零点误差等测量仪器的误差.由于这些因素对于标定指标的影响很复杂,很难准确地给出定量关系式.将系统误差整体看作一个假想的零点漂移z0,表征标定值和实际值之间存在一个恒定的偏差,其余误差的均值为0.则有z0=E(δSystem),又由于假设偶然误差均值也为0,故有z0=E(δ).用z0对标定体系进行修正,得到修正后的标定体系.
使用假想零点漂移修正理想容器法带来的系统误差,虽然可以在一定程度上减小误差的均方根值,但是只相当于对系统误差曲线进行了平移,系统误差的趋势并未得到很好的描述与消除.
2 等效液面高度标定法
2.1 等效液面高度标定法的模型描述
如前所述,诸多复杂因素造成实际储油容器和理想容器之间标定容积的误差,理想容器法将这些误差归为方法和仪器的系统误差与偶然误差的叠加.引起理想容器法中系统误差不容易定量描述,即使使用假设零点漂移的方法进行修正,仍不能很好地消除.但是,油罐注油和排油的实测数据中包含着实际储油系统的相关信息,如果能够利用油罐中液面高度和储油量的实测对应关系来构建油罐变位后的容量的标定体系,就相当于一定程度上将系统误差考虑在标定过程之中,以达到减少标定误差的目的.
在储油容器的变位过程中,当油罐中油品体积相同时,油浮子所测得的液面高度有可能发生变化.事实上,对于理想容器,可以得出液面高度变化随油罐纵向变位角α之间的对应关系.设有变位的时候,理想容器中油品的体积为VDeflection,它是发生变位后纵向变位角α和实测液面高度h0的函数,函数关系由式(2)确定.设其等效无变位油罐中的油品液面高度为he,罐中油品体积为VEquivalent,显然有

无变位时椭圆柱形储油罐内各处横截面为全等的椭圆缺形,横截面积相等.设横截面的椭圆缺形面积为S,液面高度he为椭圆缺的弓高,则S是弓高h e的函数.设d=x2-x1,则对于此时的无变位储油罐,有

将式(8)代入式(7)中,得到
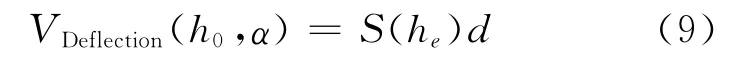
式(9)即为理想容器情况下变位实测液面高度h0对无变位等效液面高度he的换算关系式.
通过油罐注油和排油的实际数据制作出无变位时液面高度与罐内油品体积的换算查找表,并将其记作V=v(h).为了能够得到V=v(h),可以对实测的离散数据进行插值处理.研究表明,在各类插值方法中,三次样条曲线插值方法在处理油罐储油量标定问题时效果最好[6].对于变位后的储油罐的油品液面高度h0,首先通过解式(9)的方程计算出对应的无变位罐的液面高度he,再将he代入函数V=v(h)计算储油罐中油品的体积.由于v(he)是通过实测数据得到的标定体系,修正了理论计算结果,将其值记为VCorrect.
综上所述,得出纵向变位角α下的变位罐容积标定系统如下:
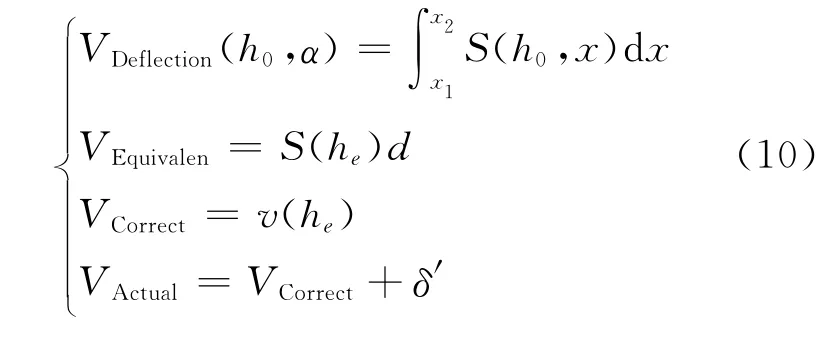
2.2 等效液高标定法的求解与误差分析
在进行等效液高转化时,所求得的等效液高是理想容器情况下的转化高度,即理想容器水平放置于变位后相同体积油品的液面高度关系.实际容器的形状、内部构造等与理想容器之间必然存在着偏差.这些因素在进行等效液高转化的计算时都没有被计算在内,所以在进行等效液高换算时,对理想容器系统的系统误差进行修正的同时又引入了因修正而产生的修正误差δCorrect.修正误差δCorrect和随机误差δAccidental合成了定标体系的总误差δ′.即

相比理想容器标定法,等效液高标定法因为计算时本身考虑到了一部分系统误差,所以得到的误差值δ′相比δ有所减少.
3 仿 真
以2010年全国大学生数学建模竞赛数据代入本文建立的模型,分别使用理想容器标定法和等效液面高度法对变位储油罐罐容表进行标定.将标定的罐容表和实测数据进行比较.
理想容器标定法求得标定值与实际值之间的误差如图3所示,经计算,均方根误差RMSE1=77.62 L.
图4为等效液高标定法标定的罐容表误差示意图.通过计算可得,利用等效液面高度标定法得到的均方根误差RMSE2=27.69 L,相比理想容器标定法的误差有所减小.

图3 理想容器标定法误差与液面高度关系图Fig.3 Relationship between error of ideal container method and liquid level
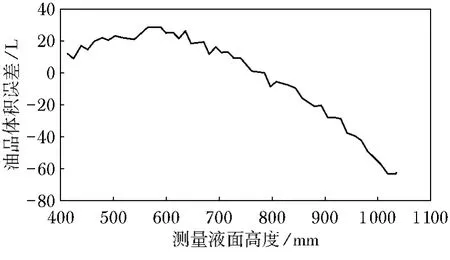
图4 等效液面高度标定法误差与液面高度关系图Fig.4 Relationship between error of equivalent liquid depth method and liquid level
4 结 论
本文提出了理想容器法和等效液面高度法.针对规则几何体,采用数值积分的方式计算其体积,避免了符号多重积分运算,在保证一定计算精度的前提下,使问题得到了简化.本文建立的变位储油罐罐容表的标定模型除了可以用来对已知变位参数的油罐进行罐容标定,还可以运用罐容实测数据,对未知变位参数的变位储油罐进行变位参数估计,有其实用价值.
[1] 管冀年,赵海.卧式储油罐罐内油品体积标定的实用方法[J].计量与测试技术,2004,31(3):21,36.
[2] 孔庆宽,季永聚,王景成.圆柱形斜卧贮液罐体的液体容重及其重心的计算[J].大连轻工业学院学报,1987(1):51-57.
[3] 徐顺福.内浮顶油罐储油计量不准的原因分析[J].油气储运,1992,1(5):48-52.
[4] 田铁军.倾斜卧式罐椭直圆筒部分容积的近似计算[J].现代测量与实验室管理,2004(1):26-27
[5] 程继元.浅谈影响油罐标定与计量的因素及其修正方法[J].石油商技,2004,22(2):33-35.
[6] 李云,任建平,宁彩林.插值算法在油罐储油量测量中的应用[J].科技情报开发与经济,2006,16(12):165-166.
Research on Volume Calibration Schemes of Tilted Oil Tanks
YUE Xiaoning 1,ANZhecheng 2,YUGuangying 3,ZHANGLingling 1
(1.School of Science,Shenyang University,Shenyang 110044,China;2.School of Information and Communication Engineering,Dalian University of Technology,Dalian 116024,China;3.School of Power and Energy Engineering,Dalian University of Technology,Dalian 116024,China)
Volume calibration of a horizontal oil tank was focused when the tank was vertically tilted.First of all,an ideal container was studied and a formula was introduced to calculate the numerical integration of the volume of oil in a tiled or not tiled regular container.The volume calculation formula was used as a calibration system to estimate the volume under practical situation.The source of deviation in ideal container method was analyzed,and another volume calibration method called the equivalent liquid depth method based on it was carried out.In the equivalent liquid depth method,the measured liquid depth in a tilted oil tank was converted into the liquid depth in a not tilted tank,and then the real-test data of a not tilted tank was used to implement volume estimation.
calibration;tank capacity;volume calculation;numerical calculation;error analysis
O 212.1
A
1008-9225(2012)01-0064-04
2011-08-28
岳晓宁(1962-),女,辽宁沈阳人,沈阳大学教授,博士.
李 艳】
