消费者有限理性选择演化模型的动力学分析

顾恩国，向 蕾，李晓东，李远平(中南民族大学 数学与统计学学院,武汉 430074)

传统消费者选择模型[1]假设消费者是完全理性的，即他们充分掌握经济系统的所有信息(如预算和价格)且具有解最优化问题的能力和意愿；而且假设消费者对指定商品的偏爱程度是不变的.这些假设对于研究消费者短期行为是合理的，但对于研究消费者长期行为就不恰当.针对这一问题，美国学者阿尔钦在消费者选择理论中考虑了有限理性思想[2]，描述了在决策机制下，经济代理人通过自适应过程如何做到完全理性.本文在假设消费者对指定商品的偏爱程度随时间发生变化，且对指定商品的购买量发生变化的情况下，建立一个描述消费者的选择和偏好变化的离散时间动力学模型，然后用映射动力系统的理论[3]分析其正不动点的存在性与稳定性，它反映消费者购买量与偏爱程度最终变化状态.最后分析其可行吸引域，它反映消费者当前购买量与偏爱程度是否合理.

1 模型的建立

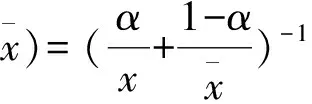
(1)

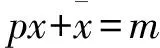
(2)

由Lagrange乘数法可得:

(3)

令:

(4)

解之得最优解应满足:

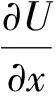
(5)

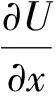
假设消费者不能或不愿意解出上述优化问题，而是根据指定商品的边际效用相对其它商品边际效用比值与商品价格之差来确定是否增加指定商品的购买量，即按照自适应过程调整其在任何时段的购买量[5]：

xt=xt-1+μ[S(xt-1)-p],

(6)

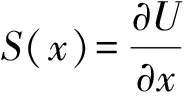
根据(1)式可以求得:

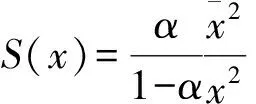
(7)

方程(6)化为：

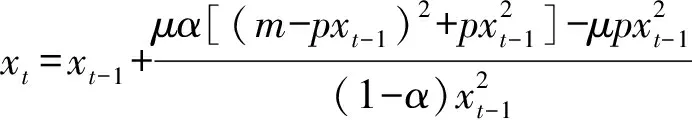
(8)

考虑过去的选择对消费的影响.消费者可能一开始慢慢喜欢某指定商品，经过一段时间后又越来越喜欢在过去期间所消费的商品，而倾向于选择在过去所消费的商品；再经过一段时间后对指定商品的偏好趋于稳定.因此假设效用函数(1)中的参变量α随时间动态变化[6]满足：

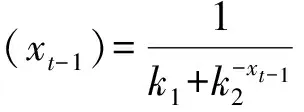
(9)

综上所述，描述消费者选择的动力学模型可以用下面的二维差分方程描述:

(10)

2 正不动点的存在性和局部稳定性分析

2.1 正不动点的存在性

(10)式可以写成映射动力系统形式:

(11)

这里′表示时间递增一个时段.

令x′=x，α′=α，系统(11)的不动点为下面非线性方程组的解:

(12)

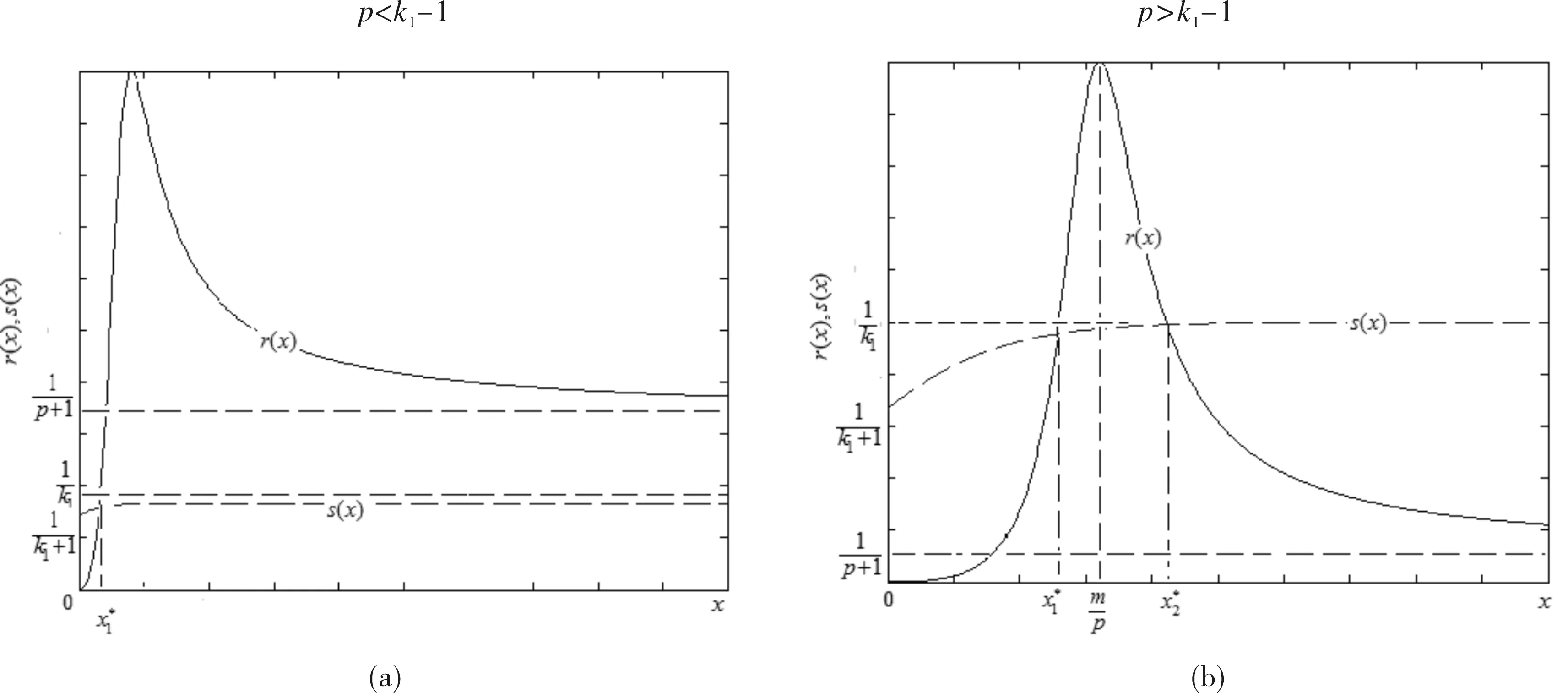
图1 系统(11)的正不动点存在性的图像表示

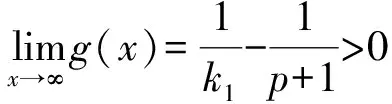
2.2 正不动点的稳定性分析和局部分叉

为了讨论系统(11)的不动点的稳定性，我们考虑系统(11)的Jacobian矩阵：

J(x,α)=

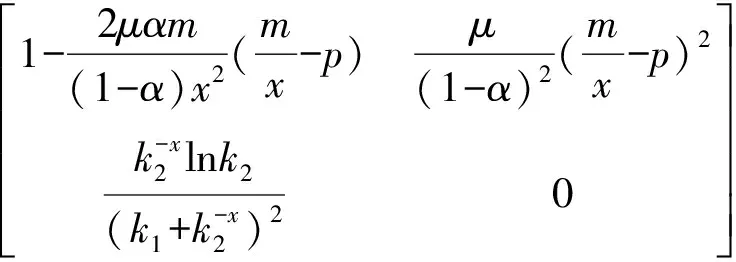
(13)

记正不动点为(x*,α*)，将该点代入(13)式中，得到对应的特征方程为：

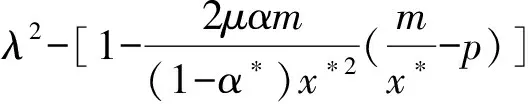
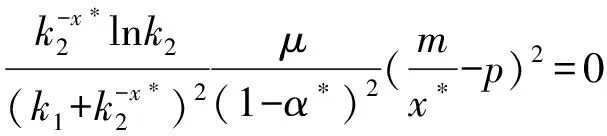
(14)

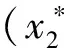
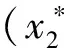
(2)系统(11)不可能发生Neimark分叉;

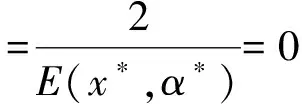
图2 系统(11)关于商品价格p和调整速度μ的一维分叉图

下面用中心流形定理讨论A1点的局部稳定性，首先将系统的不动点平移到原点，则原系统化为：

(15)

于是系统在A1=(28.9,0.1429)处泰勒展开，忽略高阶余项得到：

(16)

令X(x)=0.16x2-16.33αx+101.79α2-0.009x3+118.76α3+1.33αx2-19.06α2x，则(16)式的矩阵形式为：

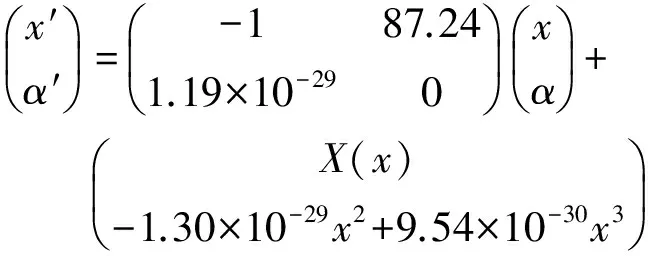
(17)

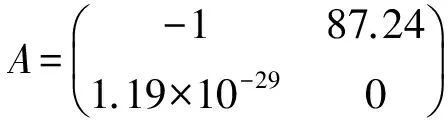
(18)

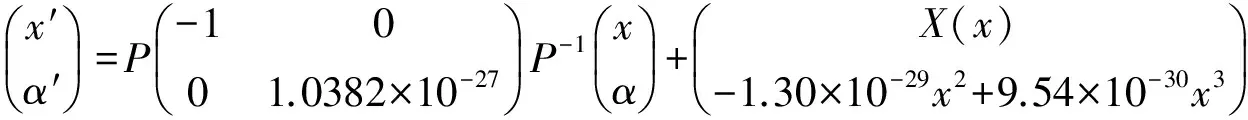
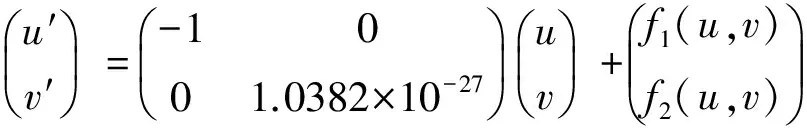
(19)

其中

f1(u,v)=0.009u3+0.16u2+0.012u2v-

0.011uv2+0.13uv-0.014v2-0.004v3,

f2(u,v)=(-0.95u3-1.3u2-2.86u2v-

2.61uv-2.86uv2-1.3v2-0.95v3)×10-29.

不妨设中心流形为Mc={(u,v)∈R2|v=h(u),h(0)=0,h′(0)=0}，假设中心流形的函数形式为：h(u)=c1u2+c2u3+o(u4)，则中心流形必须满足：h(Au+f1(u,h(u)))-Bh(u)-f2(u,h(u))=0，其中A=-1,B=1.0382×10-27.于是得到：

(20)

(21)

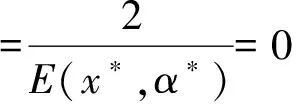
3 全局分析

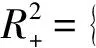
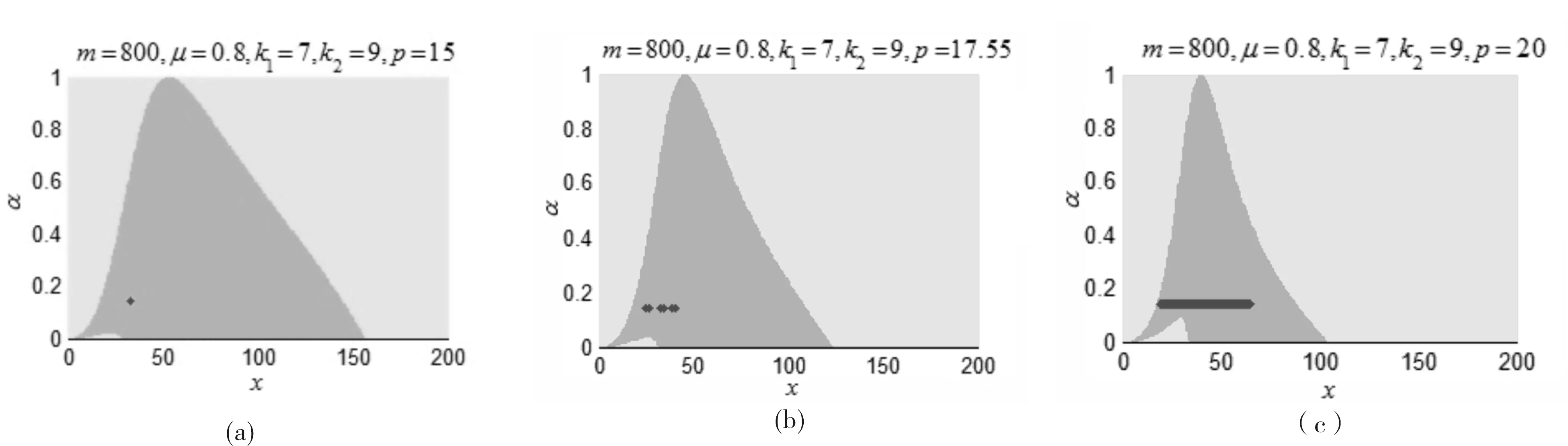
图3 当参数m=800,μ=0.8,k1=7,k2=9时，系统(11)随着商品价格p变化的可行吸引域

4 结语

本文在假设消费者是有限理性并且对指定商品的偏爱程度随时间变化的条件下，建立了消费者对指定商品选择数量和对指定商品偏爱程度演化的离散动力学模型，并对模型进行了非线性分析.我们发现指定商品的价格和消费者对指定商品购买量的调整速度的变化均可以使消费者对指定商品最终的购买量出现混沌波动.价格对消费均衡有明显的影响，消费者对指定商品最终的购买量随着价格的增加而减少，价格增加到一定水平后消费者对指定商品购买量出现随机波动，可行吸引域的面积也随价格的增加而减小，并且吸引子与可行吸引域的边界的距离也随价格增加而减小，因此商品价格的增加不利于消费者做出合理的选择.

[1]Marimon R.Learning from learning in economics[J].Economics and Econometrics :Theory and Applications，1997(1):278-315.

[2]Alchian A A.Uncertainty,evolution,and economic theory [J].Journal of Political Economy,1950 (58): 211-221.

[3]Bischi G I,Naimzada A.Global analysis of a nonlinear model with learning [J].Economic Notes,1997 (26):143-174.

[4]姜启源，谢金星，叶 俊.数学模型[M].北京：高等教育出版社，2007: 72-74.

[5]D’Orlando F ,Rodano G.Fondamenti teorici dell’ipotesi di razionalità: il ruolo dell’esperienza [J].Economia Politica,2006(23):425-452.

[6]Bischi G I ,Tramontana F.Basins of attraction in an evolutionary model of boundedly rational consumers [J].Pure Mathematics and Applications,2005,16(4):345-363.

[7]Elaydi S N.Discrete chaos [M].BocaRaton: Chapman & Hall/CRC,2000:153-168.

[8]Jury E I.Inners and stability of dynamic[M].New York: Wiley,1974:85-134.

[9]Gu Enguo.Global analysis of an ecological populational model with an external interference [J].Chaos Solitions and Fractal,2007(32): 224-233.

[10]Gu Enguo.Global bifurcations of domains of feasible trajectories: analysis of a predator-prey model [J].Int J of Bifurcation and Chaos,2006,16 (8): 2601-2613.