W-Cu合金物理性能模型及理论值计算
2011-12-31李达人蔡一湘刘祖岩王尔德
李达人,蔡一湘,刘祖岩,王尔德
(1.广州有色金属研究院粉末冶金研究所,广东 广州 510651;2.哈尔滨工业大学材料科学与工程学院,黑龙江 哈尔滨 150001)
W与Cu属于不互溶材料,传统上一般采取熔渗烧结或液相活化烧结工艺方法制备,但很难获得高致密度和优良的性能(主要为电导率,热导率和硬度值)。钨铜材料由于其具有良好的耐电弧烧蚀性和抗熔焊性等优点,已被应用于真空开关电触头材料、电热合金和高密度合金、电阻焊、电火花加工和等离子电极材料、电镦等电加工用的电极和砧块等[1-4]。
近年来,钨铜材料由于其良好的导热性能在大规模集成电路和大功率微波器件中作为基片、嵌块、连接件和散热元件,在电子器件与耐高温器件中获得了大的发展。如:电子封装材料,计算机中央处理系统、大规模集成电路的引线框架,固态微波管等电子器件的热沉基片等。“宙斯盾”系统的AN/SPY相控阵雷达,也采用了钨铜材料作为雷达微波管的热沉[5-8]。
根据钨铜材料的内部结构,国内外的一些学者分别提出了一些具有各自特色的物理模型,主要是与热物理性能有关的理论模型[9-10]。广州有色金属研究院的蔡一湘教授[11]根据其中German的互联结构模型进行了一些推导和计算,得到了热导率和热膨胀系数的理论值,但没计算电导率。本文补充了Gasik提出的微观力学结构模型,对各个物理模型下理论电导率值进行了推导和计算,并在此基础上,根据实际应用中最常见成分配比的钨铜材料(质量分数为10~50%Cu)的组织特点进行了分析筛选,确定了不同铜含量的钨铜材料所适用的模型和物理性能参数理论值。
1 有关的理论模型
1.1 体积混合物模型
对于W-Cu材料的密度和热容值,由于钨和铜两相不互溶,因此其相对密度值对显微组织结构不敏感,可简单按照复合材料混合物的计算规律来计算得到。

式中:ρW和ρCu分别为W和Cu的理论密度,mW和mCu为两相的重量百分比含量。
热容的具体公式表述如下:

式中:CCu和CW分别为金属Cu和W的物理热容值,而mCu和mW为两相的重量百分比含量。
若仅仅按照体积混合物模型来计算热导率则有:

式中:λCu,λW分别为金属Cu与W的热导率,VCu,VW为两相的体积分数。
与前面类似,钨铜看成简单的体积混合物,在颗粒分布均匀前提下,热膨胀系数可按下式计算:

式中:αCu,αW分别为金属Cu与W的热膨胀系数,VCu,VW为两相的体积分数。
1.2 German互联结构模型[11]
材料的热物理性能参数(包括热导率,电导率和热膨胀系数等)与其显微组织的结构以及应变交互作用有关。对于W-Cu和Mo-Cu等液相烧结系统,所形成的结构是互连类型,由呈现为固体颗粒的多面体骨架以及沿固体颗粒边缘分布的液相凝固态结构组成,其组织结构由图1所示。German首先提出了有关该类模型的理论参数计算公式。
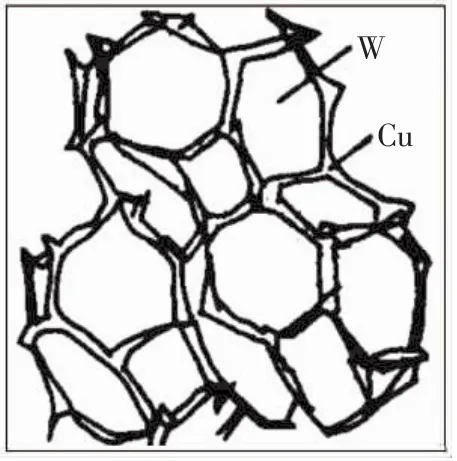
图1 W-Cu材料互联结构模型组织示意图[11]
按照German模型计算理论热导率Qcomp值有:
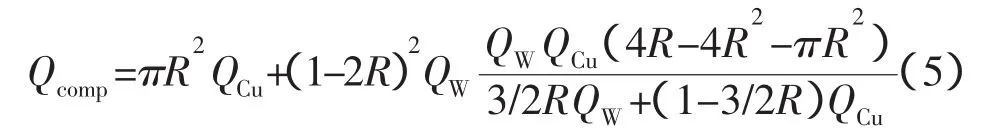
其中,R=0.0113+1.58VCu-1.83VCu3/2+1.06VCu3,VCu为铜的体积分数。
采用German模型计算热膨胀系数αcomp有:
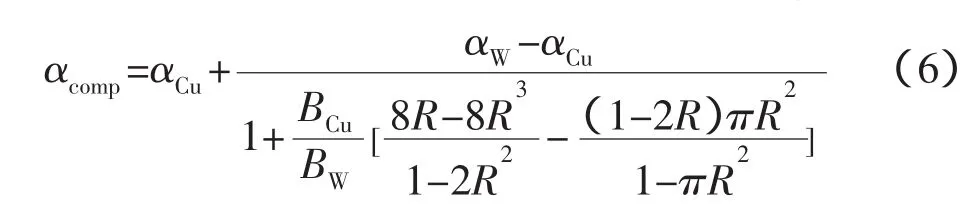
其中,R与计算热导率的公式中的R值相同,而:

式(6)与式(7)中αCu和αW分别为金属铜和钨的热膨胀系数,Bi为组元体积模量,γi为组元泊松比,Ei为组元弹性模量。
该模型的假设条件为:无应变,无孔隙和理想界面结合,为理想条件。实际上,两相CTE值差别所产生的热循环应变,杂质和内界面(相界面和各相晶格界面)对理论计算都有影响。
1.3 Gasik微观力学模型[12]
Gasik在研究W-Cu功能梯度材料的过程中提出了对其物理性能的理论计算模型。将W-Cu材料划分成许多小的微元体(Subcell),并使每个微元体中包含一个第二相(W相)且满足其体积含量VW条件。又可以把微元体称为LRVE(Local Representative Volume Elements),并通过固体力学和热力学的推导计算来表征其应力应变和物理性能。其微元体如图2所示。

图2 W-Cu材料微观力学模型LRVE图[12]
由微观力学模型推导得到的钨铜材料的理论热导率计算公式如下:
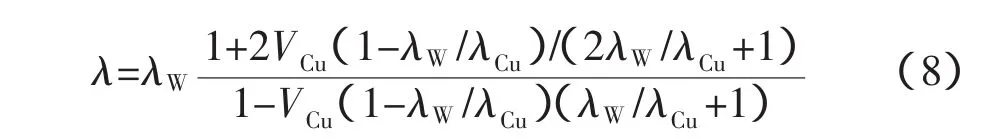
式中:λW、λCu为两相的热导率值,VCu为Cu相的体积分数。
同样采用微观力学模型来计算热膨胀系数αcomp有:

式中:αW、αCu为两相的热膨胀系数,VW、VCu为两相的体积分数,KW、KCu为两相的体积模量,μW为钨相的泊松比。
该模型的假设条件为:(1)各个微元之间是紧密完整结合的;(2)材料内部不存在孔隙,杂质或其他缺陷;(3)温度场分布均匀稳定;(4)不存在外加力场;(5)在每个LRVE微元体中第二相粒子的形状被视为立方体,其体积占微元体总体积比与其在合金中的体积含量一致。
2 计算结果与分析
为了方便计算,表1给出了所需要的钨和铜单质常用物理参数值。
2.1 密度与热容

表1 钨和铜常用的物理参数
密度与热容值按上文所述均可以用复合材料混合物计算模型的式(1)式(2)计算得到。Cu含量为10%~50%(质量分数)的W-Cu材料理论密度与热容计算值如表2所示。
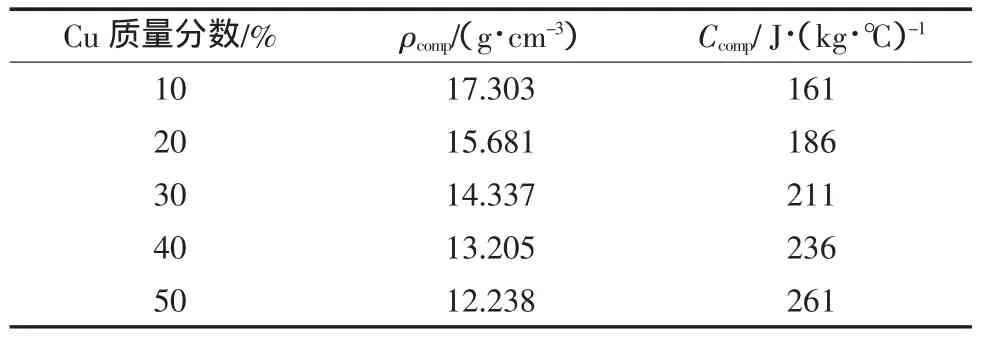
表2 不同成分钨铜合金理论密度和热容值
2.2 热导率与热膨胀系数
不同模型的热导率与热膨胀系数可由式(3)~(9)计算得到,计算值如表3,表4,表5所示。
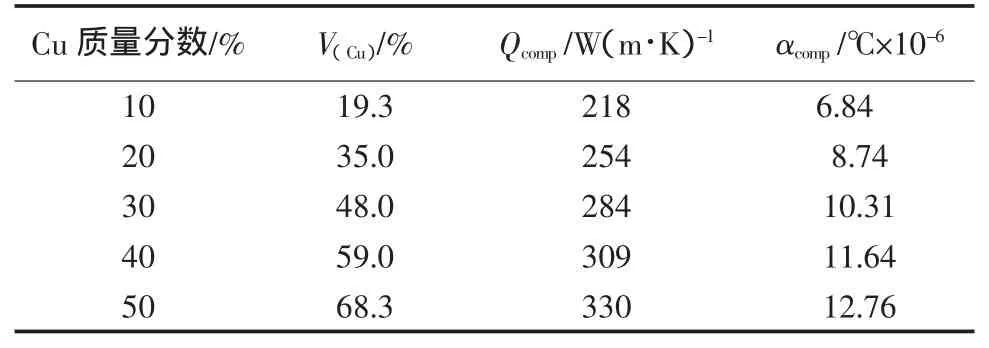
表3 钨铜理论热导率与热膨胀系数(体积混合物)

表4 钨铜理论热导率与热膨胀系数(互联结构)

表5 钨铜理论热导率与热膨胀系数(微观力学模型)
2.3 电导率
目前国内外还没有专门的文献介绍W-Cu材料理论电导率的计算方法。但是,已经证明电导率和热导率有一定的相关性和一致性,因此可以根据计算的热导率值来推导理论电导率。
1853年,德国物理学家维德曼和弗兰兹通过实验发现,在特定温度下,金属的热导率和电导率的比值是一个常数。当温度升高或降低时,金属的电导率和热导率会成比例的改变。这一定律被称作维德曼―弗兰兹定律,它是固态物理的基本定律之一。因此,也可以采用以上几个理论模型计算出的热导率值,进一步运用维德曼-弗兰兹定律来计算电导率。

式中:L为金属的洛伦兹数,K为热导率,σ为电导率。
虽然该公式一般适用仅于纯金属,但已经通过特定物理模型对钨铜材料的热导率进行了修正,因此如果再利用体积混合物定律对L值进行一定修正,该定律将在一定程度上适用于钨铜材料。
在T=293K的时候有:
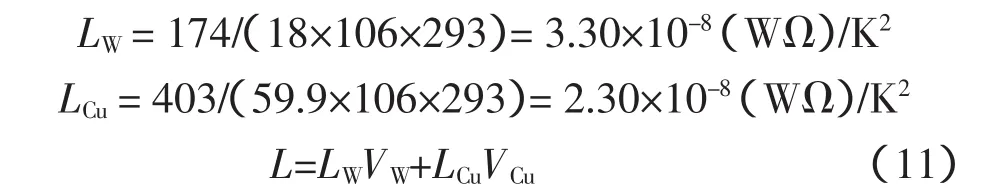
式中:LW,LCu分别为W相与Cu相的洛伦兹数,VW,VCu分别为W相与Cu相的体积分数。
通过计算得到的不同模型电导率如表6所示。

表6 钨铜理论电导率
残余孔隙的存在不可避免的要减少热导率与电导率。估算残余孔隙对热(电)导率的影响见下式:

Qrel为实际热(电)导率与理论热(电)导率的比值,ε为材料的残余孔隙率。设材料残余孔隙率为2%~5%,可推算热(电)导上限值Qactul=(0.925-0.976)Qth。
2.4 不同模型的比较
容易看出,按照体积混合物模型计算得到的电导率和热导率值偏高。因为该模型将材料看成是颗粒增强复合材料且不考虑两相间的相互作用。实际上在铜质量分数小于等于20%时,即铜体积分数小于35%时,钨铜材料应该看成类似于German所提出的模型,形成互联的结构类型,固体颗粒骨架与沿固体颗粒边缘分布的液相凝固态。因此,在该成分条件下钨铜的热导率、电导率、热膨胀系数理论值应该以German模型为准。
而对于铜质量分数为30%、40%的钨铜材料,铜的体积分数已经达到了一半甚至一半以上。此时,German模型的准确性将有所下降,应该考虑采用Gasik提出的微观力学模型来计算其理论热导率、电导率、热膨胀系数。从计算结果可以看出,此时的理论值介于German模型与体积混合模型计算值之间,在铜质量含量为40%时与体积混合模型计算值相同。
对于铜质量百分含量大于等于50%的钨铜材料,很明显可以看出,随着铜体积分数的增加,材料的性质已经发生了一定的变化。German的模型计算值已经开始偏低,而Gasik的模型计算值却偏高。而此时可以将材料近似地看成钨颗粒增强铜基复合材料,按照体积混合模型来计算近似理论值。而考虑到两相之间的相互作用,实际理论值还将低于该值。
表7为综合不同理论模型得到的钨铜材料近似理论热导率、电导率、热膨胀系数(均假设为全致密材料)。
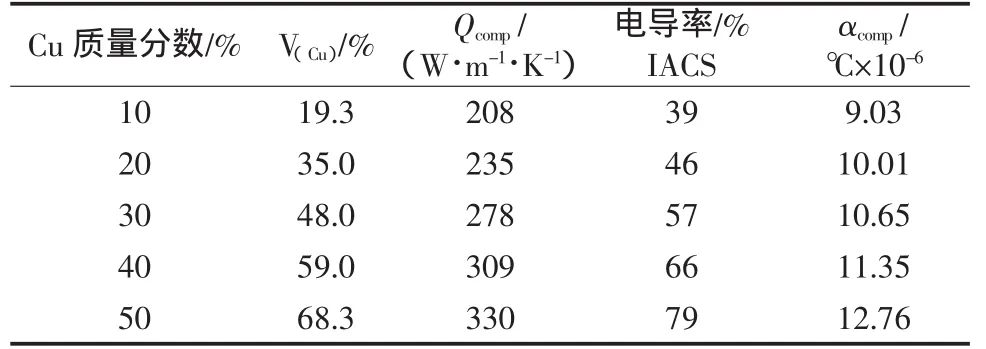
表7 钨铜材料物理参数理论值
2.5 实验值与理论值的比较
图3给出了采用热挤压法获得的钨铜合金相对密度,实验测得的电导率值,理论电导率值随铜含量变化的关系曲线。其中理论热导率值采用表7所给出的值并经公式(12)修正得到。

图3 热挤压W-Cu合金相对密度与电导率随铜含量变化曲线
从图中可以看出,在铜含量较低时实验电导率与理论值符合较好,随着铜含量的增加实验值与理论值的差别增大,实测值要低于理论值,这是因为理论值主要考虑的是孔隙率变化的影响,并对其进行了适当的修正。当铜含量增加后,孔隙率降低,此时界面反射等其他影响因素开始逐渐占据主导地位。
3 结论
(1)通过对不同组织结构模型(体积混合物,German互联结构和Gasik微观力学模型)的归纳总结,推导了不同模型下的主要物理性能参数包括密度,热容,热导率,电导率,热膨胀系数等的理论值。
(2)根据不同模型的特点进行了比较和分析,通过对不同铜含量(10%~50%)所适用的组织结构模型的讨论,选取得到了合适的钨铜合金物理性能参数理论值。
(3)将不同铜含量(20%~50%)坯料实验测得的电导率值与理论计算值进行了比较,随着铜含量的降低,两者差异减小。
[1]李云平,曲选辉,段柏华.W-Cu(Mo-Cu)复合材料的最新研究状况[J].硬质合金,2001,18(4):232.
[2]范景莲,严德剑,黄伯云等.国内外钨铜复合材料的研究现状[J].粉末冶金工业,2003,13(2):9.
[3]吕大铭.钨铜复合材料研究的新进展[J].中国钨业,2000,15(6):27.
[4]刘辉明,范景莲,刘 涛,等.细晶W-Cu合金的高温拉伸力学行为与组织演变[J].中国钨业,2011,26(1):38-41.
[5]刘正春,王志法,姜国圣.金属基电子封装材料的进展[J].兵器材料科学与工程,2001,24(2):49.
[6]余建芳.钨的应用—从电子材料到军事弹药[J].中国钨业,2001,16(2):39-41.
[7]冯 威,栾道成,王正云,杨丽蓉.影响钨铜复合材料烧结的致密度的两个因素[J].中国钨业,2007,22(5):23-26.
[8]吕大铭.粉末冶金钨钼材料发展的国内外近况[J].粉末冶金工业,1997,7(3):40-43.
[9]German R.M.Phase Equilibria Effect on Enhanced Liquid Phase Sintering of W-Cu[J].Metall.Trans.1993,24A:02369.
[10]Gasik M.M.,Kaj R.Evaluation of properties of W-Cu functional gradientmaterials bymicromechanicalmodel[J].Computational Materials Science,1994(3):41-49.
[11]蔡一湘,刘伯武,谭立新.钨铜系合金的热物理性能模型及计算[J].粉末冶金材料科学与工程.1997,2(1):11-14.
