外汇结构性存款的价值分解与定价方法分析

刘凤琴,张 强

(1.浙江财经学院信息学院,浙江 杭州 310018;2.浙江财经学院金融学院,浙江 杭州 310018)

一、引 言

外汇结构性存款在外汇资产保值增值、银行发展创新中间业务等方面具有重要的作用,近年来在我国发展速度非常迅猛。但是,随着美国次贷危机的爆发,许多外汇结构性存款因其联动货币利率的不利变化,不但难以实现预期收益,而且由于汇率变动而可能导致本金的损失。同时,与国外银行相比,我国银行在外汇结构性存款业务中往往是作为经销商的角色出现,即便是自行开发的产品也大都雷同,在未来的竞争中必将处于劣势处境[1]。因此,研究外汇结构性存款的内在价值构成、定价技术对于我国商业银行在结构性产品的开发和风险管理等方面具有重要的理论与实际意义。

根据当前银行所发行的外汇结构性存款的合约条款,其最全面的价值构成可以表述为:外汇结构性存款价值=本金+固定收益价值+浮动收益价值+可赎回权-可回售权[2]。在目前应用的各种外汇结构性存款中,有些相对简单,仅仅包含其中的一个条款;有些则相对复杂,包含了上述公式中所有条款。本文在此基于以下两方面考虑,选取带有提前赎回或回售特征的范围累积外汇结构性存款作为研究对象,分析探讨外汇结构性存款的价值结构及基本定价方法框架。从理论方面来讲,该结构性存款包含了影响外汇结构性存款定价的全部三个基本要素;所以,选择对该产品定价可以完整地分析出各个因素对于产品价值构成的影响,具有重要典型的理论意义。从实际方面考虑,基于增加盈利空间的需要,产品设计者往往偏好于设计出一些结构比较复杂的结构性存款,而当前市场上出现越来越多具有可提前赎回或是回售特征并带有奇异期权结构性存款也证明了这一点;与此同时,从与Libor利率联动的角度可以得出,对此产品的定价进行分析也有助于确定我国Shibor利率服从何种随机过程以及以Shibor利率联动的人民币结构性存款定价的研究具有重要的实践意义[3]。

二、外汇结构性存款的价值构成分解

(一)普通欧式外汇结构性存款的价值构成分析

假设该外汇结构性存款的存续期为 [T0,Tm],其中T0为当前日期,Tm则为该产品的到期日。此外,我们考虑一个完整的概率空间 [Ω,F,Ω],其中,Ω为非空集合,代表了所有可能发生的经济事件和信息。F作为Ω的子集族被称为σ-代数,其代表相应时刻所得到的经济信息,Q代表了相应的概率测度,则不包含提前赎回特征的产品价值可表示为:

其中,VNC(Tj)代表Tj时刻不可提前赎回条件下的外汇结构性存款的理论价值,K(Ti)表示该产品的每个利息支付点发行者向投资者支付的利息,根据结构性产品衍生产品特征,此处利息恰恰是产品设计者偏好的创新之处,因为,该处利息支付可以看做是产品内含衍生工具的盈亏收益函数。以本文定价产品为例,该利息即为各固定期限内范围累积期权在相应利息支付点的盈亏收益。同时,本文设定当满足i>m时,(…) =0。因此,VNC(Tm) =1/B(Tm)。

(二)具备提前赎回特征的价值构成

假设该产品具有提前赎回特征时,根据以上分析,其理论价值可以表示为[4]:

其中,ξ(τ)表示该产品各个停时的顺序。因此,具有可提前赎回特征的外汇结构性存款主要有三部分组成:零息债券、由范围累积期权所得到的浮动收益以及可提前赎回权。其中,VNC(T0)表示零息债券与范围累积期权的价值之和,C1(T0)代表可提前赎回权的价值。

从发行者银行追求利润最大化的角度来讲,肯定希望未来所需支付的现金流越少越好,即V值越小越好。同时,VNC(T0)可以看做一个普通的附息债券,其理论价值主要取决于未来标的资产价格的走势。所以,如何选择最优执行点以达到V值最小化,主要是通过可提前赎回价值C1(T0)的最小化所决定。可提前赎回期权是一种具有有限个执行点的百慕大式看涨期权,其盈亏函数可以表示为以τk时刻为起始日的不可提前赎回债券的价值与τk时刻产品面值的现值之差[5]。此处,可以把VNC(τk)看做资产价格,而把1/B(Tτk)看做该期权的执行价格。为了计算该期权价值,首先定义该提前赎回期权的盈亏收益函数Z(Tj),即

从上述公式可以看出,如果该期权持有者执行该期权,那么相当于该持有者收到了附息债券所产生的现金流现值,同时支付面值的现值。于是,本文引入一个Snell envelope(U(Tj))j=k…m来代替该期权盈亏函数过程 (Z(Tj))j=k…m。同时,为了理论完整性及实际经常出现产品开始几期内不允许执行该期权现象,令k表示产品允许提前赎回的起始点,则 (U(Tj))j=k…m具有以下公式:

上式是一个最优停时问题,可以运用向后动态规划方法进行求解。首先,在产品到期日Snell envelope(U(Tj))j=k…m为零,也就是说,在产品到期日,期权没有价值。在产品可开始执行点到产品到期日 [Tk,Tm)的这段时间内,该提前赎回价值为持有价值Γ (Tj) =E[U(Tj+1)|FTj]和执行价值Z(Tj)两者之间的最大值。公式表达即为:

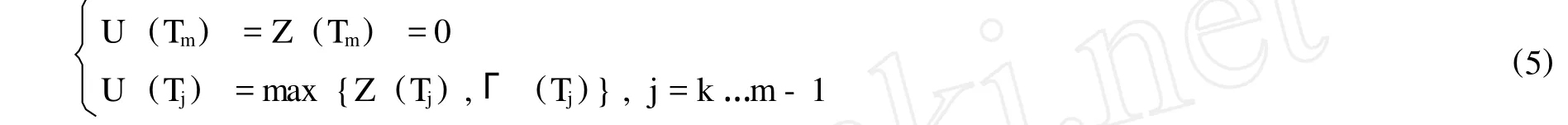
所以,在T0时刻,该提前赎回权的价值为:

其中,第一个等号是从Snell envelope U(Tk)来解释的,而第一个等号则是从最优停时处产品贴现值的角度来解释的。因此,具有可提前赎回特征的外汇结构性存款的价值为以奇异期权盈亏函数利息支付的附息债券与可提前赎回权价值之差额,即:

(三)具有提前回售特征的外汇结构性存款价值构成分解

上节主要是从银行的角度来进行分析的,同理对于投资者能够单方面终止外汇结构性存款合同的权利则被称为可提前赎回权,这部分针对该类外汇结构性存款价值构成进行分析。

从投资者追求利润最大化角度,肯定希望未来所得现金流越大越好,那么具有以下公式[6]:

如果希望产品未来产生现金流越大越好,那么就必须使V越大越好。同时,VNC(T0)可以看做一个普通附息债券,其理论价值主要取决于未来标的资产价格走势。所以,如何选择最优执行点使V2值达到最大化,主要通过可提前回售价值C2(T0)所决定。可提前回售期权是一种具有有限个执行点百慕大看跌期权,其盈亏函数可以表示为以τl时刻产品面值现值与τl时刻为起始日的普通债券价值之差。此处,可把1/B(Tτl)看做该期权执行价格而把VNC(τl)看作资产价格。为计算该期权价值,首先定义该提前回售期权盈亏收益函数:

从上述公式可以看出,如果该期权持有者执行该期权,那么相当于该持有者收到产品面值的现值,同时支付普通附息债券所产生的现金流现值[7]。于是本文引入一个Snell envelope(U(Tj))j=k…m来代替该期权盈亏函数过程 (Z(Tj))j=k…m。同时,为了理论完整性以及实际过程中经常出现产品开始几期内不允许执行该期权现象,令k表示产品允许提前回售的起始点,则 (U(Tj))j=l…m具有以下公式:

上式是一个最优停时问题,可以运用向后动态规划方法进行求解。首先,在产品到期日Snell envelope(U(Tj))j=l…m为零。在产品可开始执行点到到期日 [Tl,Tm)内,该提前回售价值为持有价值Γ (Tj) =E[U(Tj+1)|FTj]和执行价值Z(Tj)两者之间的最大值,公式为:

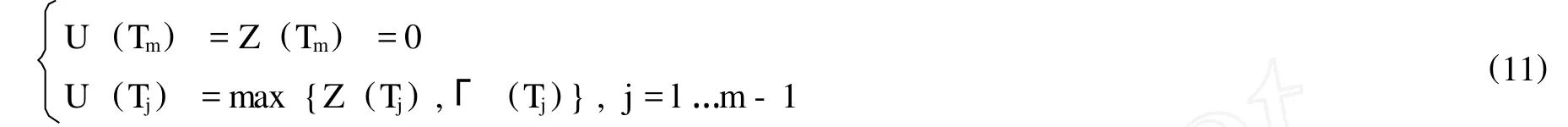
所以,在T0时刻,该提前回售权的价值为:

其中,第一个等号是从Snell envelope U(Tl)来解释的,而第一个等号则是从最优停时处产品贴现值的角度来解释的。因此,具有可提前回售特征的外汇结构性存款的价值为以奇异期权盈亏函数利息支付的附息债券与可提前回售权价值之和,即:

(四)具有可提前赎回和回售特征的混合外汇结构性存款价值构成分解

上述两部分主要从产品发行者和投资者两个角度讨论了带有提前赎回或是回售特征外汇结构性存款价值构成。但从实际情况来讲,产品设计者往往偏好于同时带有可提前赎回和回售特征。所以,这部分针对同时带有以上两个特征的产品进行阐述说明。在上述两种产品定价分析基础之上,具有可提前赎回和回售特征的混合外汇结构性存款价值为:外汇结构性存款价值=零息债券+浮动收益+可提前赎回价值-可提前回售价值。利用公式表示即为:

其中,VNC(T0)、C1(T0)以及C2(T0)分析与前面相同。基于以上分析,范围累积外汇结构性存款本质上是一个利率衍生产品的组合。当讨论其定价问题时,主要按照上述所阐述的方法将产品进行价值构成分解,然后将各个组成部分的价值进行加总。

三、附息债券部分的定价理论与方法

根据理论分析,该产品价值构成中的附息债券价值主要由零息债券部分与浮动收益所决定,其中,各期浮动收益即是相应期间内范围累计期权的盈亏函数[8]。

(一)零息债券部分

外汇结构性存款中具有零息债券特征的组成部分定价方法与普通零息债券定价原理相似。因此,该部分理论价值表现为该产品面值的现值。但是需要强调的是,进行面值贴现时,贴现率如何确定。基于风险中性定价原理,一般简单处理方法主要是设定其为国债利率,并假设其在短期内不变。但是,由于该类外汇结构性存款的期限基本都在一年以上,单纯假设贴现率不变不符合实际情况。所以,需要用一定的利率模型来模拟贴现率的变动[9]。由于该类产品联动标的变量常常为3个月美元Libor利率,而且数据获取比较方便。所以,本文采用3个月美元Libor利率作为该零息债券部分的贴现率,其价值可以表示为:

其中,Fi(Ti-1)表示在 [Ti-1,Ti]区间内,以Ti-1为期初时刻的远期利率,Δ为时间区间的长度,即为Ti与Ti-1之差。

(二)浮动收益部分

该外汇结构性存款的浮动收益部分即为范围累积期权的盈亏函数,所以,对该部分进行定价的基础就是需要对范围累积期权的组成部分——数值期权的价值进行确定[10]。然后根据产品结构原理,将一段期限内的所有数值期权价值加总即可得到该产品浮动收益部分的价值。目前,运用于金融衍生产品定价过程中的数值分析方法主要有网格分析技术和蒙特卡罗模拟方法。蒙特卡罗模拟方法能够解决以上网格分析方法的不足,从而成为该类期权各种定价方法中最为有效的数值计算方法[11]。首先,蒙特卡罗模拟通过输入假定条件以及数千次反复模拟得到数千条模拟路径,在相应的测度下,范围累积期权的价值即为各条路径下盈亏函数的平均值。这种定价方法比起网格方法和解析方法都要简单方便。其次,蒙特卡罗模拟方法与期权标的资产维数独立,能够解决网格分析方法中容易出现的“维数灾难”问题。最后,随着蒙特卡罗模拟次数的增加,该期权价值将会趋向收敛到一个稳定的值,可以避免网格定价方法结果的发散性问题。基于以上分析,拟采用蒙特卡罗模拟方法对该外汇结构性存款的浮动收益部分即范围累积期权进行定价分析。

四、可提前赎回权和可提前回售权部分的适应性定价方法

(一)结构性存款中期权价值构成分析

根据上述价值构成分析,该外汇结构性存款所内含的可提前赎回权和可提前回售权可以分别归类为可变执行价格的百慕大式看涨期权和看跌期权。由于蒙特卡罗模拟方法的前向性,一度不能将该方法运用到百慕大式期权定价过程中去。一些学者提出了多种美式衍生产品蒙特卡罗定价方法,如随机树方法、状态分层方法、随机网格方法、策略迭代法和基于回归的逆向推导方法,而基于回归的逆向推导方法事实上是广义上随机网格方法的一种特殊情况,理论上讲其应用性更为普遍,计算量与其他方法相比也减少很多。所以,本文认为基于回归的逆向推导方法是解决两个百慕大式衍生证券价值的合理手段。

根据上述分析,该类期权的价值迭代表达式可以用以下公式表达:

其中,U(Ti)为Ti时刻该类期权的价值函数,Z(Ti)为Ti时刻该类期权的盈亏函数,即执行价值,Γi为Ti时刻该类期权的持有价值。

(二)持有价值计算的一般过程分析

根据回归计算方法,确定该期权持有价值的公式为:

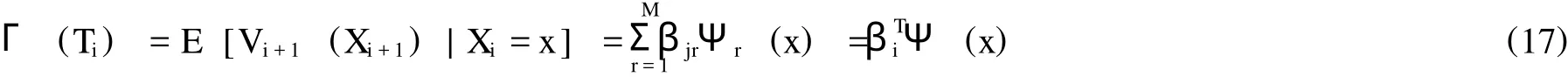
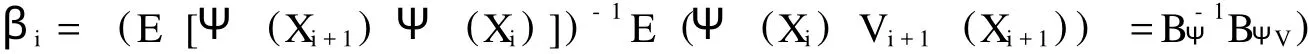
其中,^βΨ和^βΨV实际上是在BΨ和BΨV中选取了有限个元素而组成的向量。所以,当已知一对连续点 (Xij,Xi+1,j的情况下,

(三)持有价值的价值函数逆向迭代方法及最小二乘蒙特卡罗模拟

1.价值函数逆向迭代方法

在此,利用标的资产所服从的具有马尔可夫性质,模拟出b条独立的资产价格变动路径 {X1j, X2j,…,Xmj},j=1,2,…,b表示路径条数,而m表示该百慕大式衍生证券在相应路径所能够执行的时间点。根据该方法逆向推导特征,该方法步骤为[12]:

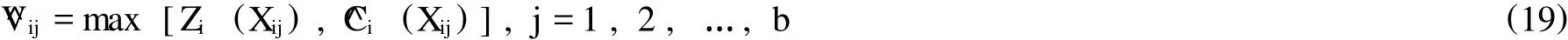
最后,按照上述计算方法,在每一条路径上,都从m-1一直逆推到第一个可执行点,然后将各条路径的最后值加总求平均,即可得到该衍生证券理论价值:

2.最小二乘蒙特卡罗方法 (LSM)

在此,利用标的资产所服从的具有马尔可夫性质的随机过程,模拟出b条独立的资产价格变动路径 {Xij,X2j,…,Xmj},j=1,2,…,b表示路径条数,而m表示该百慕大式衍生证券在相应路径所能够执行的时间点。根据该方法的逆向推导特征:

首先计算最后执行点的期权价值函数。由于该产品在最后一期必定执行,所以,该时间点处的期权持有价值为零,那么,其执行价值就等于期权价值函数,即^Vmj=Zm(Xmj),j=1,2,…,b。

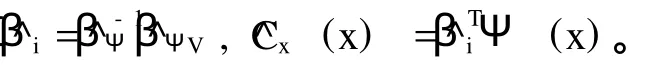
最后,按照上述计算方法,在每一条路径上,都从m-1一直逆推到第一个可执行点,然后将各条路径的最后值加总求平均,即可得到该衍生证券理论价值:

3.两种方法比较分析

首先,从回归计算中所选用的因变量的角度,价值函数逆向迭代方法在运用回归方法计算回归系数时所使用的因变量是^Vij=^Ci(Xij),相反,LSM方法使用的因变量是^Vij=^Vi+1,j。

其次,从任意可执行时点处的价值函数的角度,价值函数逆向迭代方法选择执行价值与回归方程所得的价值之间的最大值作为该可执行点的价值函数;相反,LSM方法在执行价值与回归方程所得价值比较中,如果该回归值大于执行价值,期权不会执行,则选择以该时刻点为百慕大式期权起始时刻的最优执行时点处执行价值的贴现值作为该执行点的价值函数。

第三,从判断执行点角度,价值函数逆向迭代方法主要是从最后点开始,从后往前一次判断,最后求出期初可执行点的衍生证券价值。相反,最小二乘蒙特卡罗方法认为,如果在某个执行点处该衍生证券的执行价值为负,那么,执行者将不会在此时间点提前执行该期权。如果执行价值为正数,则继续按照上述方法进行比较计算。

最后,从两种方法的定价效果角度,价值函数逆向迭代方法所得结果与真实值相比为上偏,即,当i→∞时,^Ci(Xij)是Ci(Xij)的无偏估计量,即:E[^Ci(Xij)|Xij]=Ci(Xij)。两边取期望值,再根据Jensen不等式,即使假设其持有价值估计值^Ci(Xij)为相应真实值Ci(Xij)的无偏估计,但是该方法所得到最终定价结果^Vij还是大于该类期权真实价值Vij,即所得结果为上偏。相反,LSM定价结果与真实值为下偏,即:^Vi,j=Zi,j1{Zij≥^Cij}+Vi+1,j1{Zij<^Cij}。两边取期望可知,LSM方法所得的最终定价结果大于该类期权的真实价值,那么理论价格将低于其真实价格。

4.两种方法结合的改进模式设想

根据上述分析,两种方法单独使用都未能得出一个较为准确的定价结果,所以有必要对其方法进行改进。所以,本文将设想采用以下方法对百慕大式衍生证券进行定价:首先,基于LSM方法的下偏性,利用该方法的逼近法则,我们将在有限模拟数量的情况下,选择该方法的计算结果实现最大值的基本函数类型和数量。在此基础之上,将上述结果运用到价值函数逆向迭代算法中去,最终实现最优定价结果。

五、结束语

本文主要根据金融工程分解组合原理,首先分析了影响外汇结构性存款价值的三个基本因素;其次,确定本文所研究的外汇结构性存款理论与实际原因,提出该产品价值的代数解析公式;最后基于该产品各个部分的性质特点对相应的定价理论方法进行阐述,通过系统的论证,得出以下结论:

(1)选择具有可提前赎回或回售特征的外汇结构性存款为研究对象,在理论上具有典型意义。同时,该产品的定价过程在研究我国Shibor利率服从何种随机过程,以及以Shibor利率联动的人民币结构性存款定价分析具有重要的实践意义。

(2)基于解析分析方法的复杂性以及网格技术方法由于多变量和多执行点而导致的“维数灾难”问题,本文利用蒙特卡罗模拟方法计算外汇结构性存款的附息债券部分的价值。

(3)基于价值函数逆向迭代方法和最小二乘蒙特卡罗方法定价结果的上偏性和下偏性,本文将两种方法进行结合,即先由最小二乘蒙特卡罗方法得出最佳基本函数类型数量,然后在上述结果之上利用价值函数逆向迭代方法进行产品定价,来对外汇结构性存款价值构成中的可提前赎回权或是回售权进行定价。

[1]颜忠田.结构型商品评价与分析-以逆浮动利率连结商品与汇率连结商品为例 [D].台湾政治大学学位论文,2007.

[2]郑振龙,康朝锋.中国利率衍生产品定价与保值 [M].北京:北京大学出版社,2006.

[3]张睿.外汇结构性存款的合约设计和定价分析 [M].厦门:厦门大学出版社,2005.

[4]Stefan Burth,Thomas Kraus,Hanspeter Wohlwend.The valuation of structured products:empirical finding for the swissmarket[C].ssrn. 2001.

[5]Line Grinden Quinn.Recommending structured products as investment strategy[D],2009.NHH

[6]Pavel A.Stoimenov,SaschaWilkens.Are structured products fairly Priced?An analysisof the Germanmarket for equity-linked instruments[J], Journal of Banking&Finance,2005.

[7]Sascha Wilkens,Carsten Erner.The pricing of structured Product-an empirical investigation of the Germanmarket[J].ssrn.2003.

[9]Damiano Brigo,Fabio Mercurio.Interest ratemodels:theory and practice[M].Springer,2001.

[10]Vishal Subandh.Do structured products give equity like returns?An empirical analysis in the UKmarket[D].Cranfield University,2007.

[11]Longstaff F.A,E.S Schwartz.Valuing American options by simulation:A simple least-squares approach[J].Review of Financial studies,2001,(14):113-147.

[12]Egloff D.Monte Carlo Algorithms for Optimal stopping and statistical learning[J].Annualsof Applied Probability,2005,(15):1-37.