卫星制导炮弹脉冲修正矢量的计算方法研究

戴明祥，杨新民，易文俊

（南京理工大学 瞬态物理重点实验室，南京210094）

利用成本相对较低的脉冲侧喷发动机提供操纵力的控制系统取代结构复杂、价格不菲的舵机系统将是发展灵巧弹药的理性模式之一.近年来，脉冲修正属于热点研究领域，国内外研究学者对此做了大量研究工作，并在导引律、制导控制策略、控制方式、脉冲系统稳定性等方面取得了可喜成果.HABLANI比较了利用脉冲控制的零效脱靶量导引律（ZEM）和脉冲比例导引律（PPN）[1]；文献[2]提出了脉冲修正动态稳定性条件；文献[3]在脉冲式末制导子弹导引律中提出了零效脱靶量比例导引律；徐劲祥对脉冲修正迫弹修正方案进行了研究，提出了四象限修正方案[4]等.但对于卫星制导弹药脉冲修正矢量计算方面的研究较少.

对于脉冲发动机控制系统来说，脉冲发动机有脉冲推力大，作用时间短，点了即用，单发控制量较大且数量有限等特点.正是基于上述特点，在脉冲发动机控制系统的灵巧弹药中，需保证单发发动机调控修正最优（即不出现修正过量），而脉冲发动机单发控制量较大，若不正确计算出单发脉冲修正矢量，很难实现脉冲发动机的调控最优.

1 模型建立

1.1 发动机模型建立

设脉冲侧喷发动机的推力轴心与弹丸质量中心重合，如图1所示.

图1 脉冲发动机安装位置

设共计N台发动机周向均布，如图2所示，Ox1y1z1为弹体坐标系.每台发动机之间的间隔角度.设0＃发动机位于弹体坐标系的Oy1轴上，顺弹体旋转方向依次定义1＃，2＃，…，N－1＃发动机，则第i＃发动机与Oy1轴的角度为

图2 脉冲发动机安装径向分布

1.2 坐标系转换关系

地面坐标系xyz[5]与大地固连，不考虑地球自转和曲率影响，将其看为惯性坐标系.弹道坐标系x2y2z2随弹丸速度矢量的改变而改变，需将弹道系坐标转换为地面系坐标，即：

式中，θ为弹道倾角，ψv为弹道偏角.

2 问题分析

2.1 卫星导引脉冲修正弹药控制原理

基于卫星导引的脉冲修正弹药控制系统主要由卫星虚拟导引头、滚转测量机构、弹载计算机（包括弹道解算器和决策控制机构）、脉冲发动机组和灵巧弹丸组成.其控制系统的设计如图3所示.

图3 基于卫星导引的脉冲修正弹药控制系统组成

在弹丸自由飞行过程中，卫星虚拟导引装置实时给出弹丸空间位置和速度矢量信息.弹道解算器根据上述信息，代入相关气动力参数和气象条件，解算出弹丸落点，与目标点坐标比较得到落点偏差；滚转测量机构给出脉冲发动机组各发动机位置信息.根据落点偏差和发动机位置信息，决策控制机构需计算出发动机点火与否和点火的发动机编号.在此过程中，决策控制机构必须计算出各发动机的脉冲修正矢量，从而作出最优决策.

2.2 弹道解算

根据卫星虚拟导引装置给出的实时空间位置信息（x，y，z，v），以此作为炮口参数，建立弹丸质心运动方程组[5]，并代入相关气象条件，利用数值计算方法（如龙格－库塔法）联立求解微分方程组，得出弹丸自由飞行落点.同时，弹道解算还给出了弹丸剩余飞行时间tr和落点速度矢量vt.

3 脉冲修正矢量的计算原理

理想条件：①脉冲发动机工作期间，弹体转速恒定；②脉冲发动机工作时间和作用力大小一定（即总冲大小一定），作用力瞬间产生、瞬间消失；③脉冲发动机工作对弹体姿态无影响，弹体中心轴线始终与速度矢量线重合.

3.1 脉冲平均推力矢量计算

脉冲发动机工作时间极短，故将脉冲推力矢量合成为平均推力矢量.在某时刻t0决策控制机构给出第i＃发动机的点火指令（设脉冲发动机点火延迟时间为τ），则经过时间τ后第i＃发动机点火工作.设ts为发动机工作持续时间，F为脉冲推力大小，ωx为弹体转速.图4中，ατ为点火延迟弹体旋转角度，αω为发动机工作时弹体旋转角度，γv为弹丸速度倾斜角.

脉冲平均推力矢量方向与弹道坐标系Oy2轴的夹角pi为

此刻弹道坐标系下的脉冲平均推力方向单位向量IFa为

脉冲平均推力矢量大小为

图4 脉冲发动机工作图

3.2 运动的分解

由于脉冲发动机冲量大小有限，一般为几十或上百N·s，则单个脉冲发动机对弹丸作用产生的速度分量为几m/s，对弹丸自由飞行的气动力影响很小，可以忽略不计.

如图5所示，假定在某空间位置A第i＃号发动机接受到点火指令，产生的平均推力矢量如式（2）、式（3）所示.将弹丸质心运动分解成沿平均推力矢量方向先加速后匀速的直线运动和无控弹道的自由飞行运动.在A点，由卫星虚拟导引头给出空间信息（x，y，z，v），经弹道解算器数值解出落点M的位置（xM，yM，zM）、自由飞行剩余时间tr和落点速度矢量vt.

1）直线运动.

在发动机工作期间，受持续恒定脉冲平均推力作用，弹丸作匀加速运动；当发动机作用完毕后，弹丸保持匀速直线运动.脉冲发动机产生的速度分量Δv为

式中，aFa为脉冲平均推力产生的加速度.

故经过时间tr后，沿脉冲平均推力矢量方向上的位移s为

式（6）和式（4）忽略了弹丸沿推力矢量方向横向移动的空气阻力的影响.

图5 脉冲修正矢量计算图

2）无控弹道的自由飞行运动.

由于忽略了速度分量对自由飞行气动力的影响，则自由飞行运动的一切参数不变，其运动轨迹与2.2节弹道解算描述的运动轨迹完全一致，故经过时间tr后，弹丸将会位于无控弹道自由飞行的落点M，飞行速度为无控弹道落点速度vt，其在弹道系中的坐标为（vt，0，0）.

3.3 位移的合成

如图5，经过时间tr后，直线运动的位移为lMC，则有：

无控弹道自由飞行运动的位移为lAM，则两独立运动的合成位移lAC为

则在位置A，第i＃发动机接收到点火指令，经时间tr后，弹丸将运动到C点，设C点坐标为（xC，yC，zC），速度矢量vC为（vCxvCyvCz），则有：

式中，θ0、ψv0分别为弹丸在A点时的弹道倾角和弹道偏角.

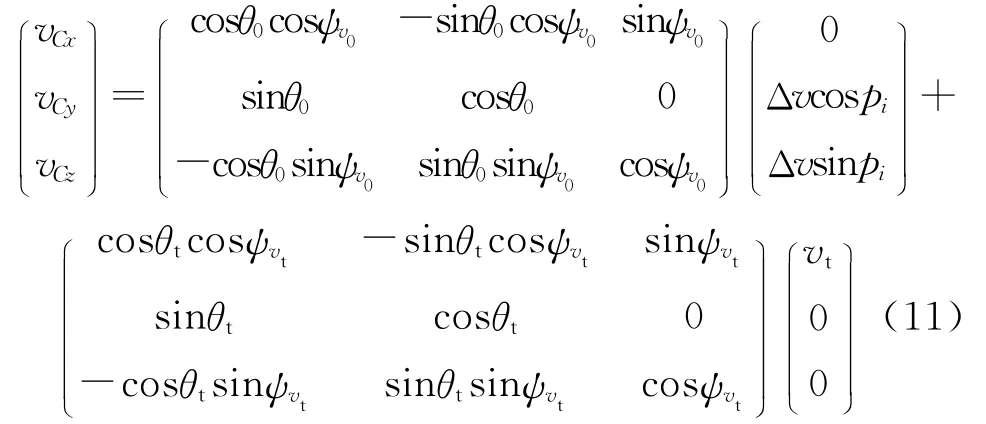
式中，θt、ψvt分别为无控自由飞行落点M的弹道倾角和弹道偏角.

3.4 脉冲修正矢量计算

由式（10）得出C点位置，由于单发发动机调控能力有限，直线运动位移s一般为几十或上百m，则C点至修正弹道落点距离很短.假定弹丸在C点附近的运动为直线运动（即此时忽略重力影响）.

脉冲修正矢量：脉冲发动机修正弹道在无控弹道落点水平面上的交点与无控弹道落点之间的方向向量.如图5中的lMM′，M′为修正弹道落点.

设M′点 坐标为（xM′，yM′，zM′），则lCM′//vC，故lCM′＝kvC，得：

由脉冲修正矢量定义知：

联立式（13）、式（14）解出：

则脉冲修正矢量lMM′为

式中，s、pi、Δv由式（6）、式（1）、式（4）给出；θ0、ψv0由卫星虚拟导引装置给出；vt、θt、ψvt由弹道解算器给出.

4 单发脉冲发动机调控能力分析

脉冲发动机调控能力为脉冲发动机修正矢量的模，用R表示，即R＝｜lMM′｜.

4.1 简化处理

对于无控弹丸气动外形，其静稳定裕度一般较大，无控自由飞行弹道弹道偏角极小，可以忽略不计，即ψv0≈ψvt≈0，则sinψv0≈sinψvt≈0，cosψv0≈cosψvt≈1.由式（16）得：

Δv一般为几 m/s，vt一般为几百 m/s，Δv为小量，则有：

将式（18）代入式（17）得：

4.2 单发动机调控能力分析

对于指定弹道，θt一般保持不变，即可认为θt为常量.联立式（1）、式（6）、式（20）知单发动机修正能力与发动机推力大小F、发动机作用时间ts、弹体转速ωx、弹丸剩余飞行时间tr、发动机位置（γv＋αi）、发动机作用时刻的弹道倾角θ0有关.

对指定弹道上某点某时刻发动机的调控能力进行分析，则弹道参数（ωx，tr，θ0，θt）、发动机参数（F，ts）都为常量，则此时发动机调控能力只受发动机位置的影响，即式（20）只有pi为变量.设得：

5 发动机最优点火决策的设计

设t0时刻，卫星导引头给出该时刻的位置信息（x，y，z）、速度矢量v，则弹载计算机通过弹道解算可得弹丸落点M（xM，0，zM），得目标点坐标MT（xMT，0，zMT）.其导引偏差矢量为lMMT＝（xMT－xM0zMT－zM）.此时第i＃号发动机脉冲修正矢量lMM′i可由式（19）求得.

则第i＃号发动机点火决策条件为

式中，λ为圆概率误差Ecp的修正系数；δ0为相角决策阈值.其决策区域见图6的阴影区域.

图6 点火决策区域

6 仿真验证

6.1 脉冲修正矢量验证

选取某典型迫击炮弹典型弹道，间隔取4个特征点位置作为起控点，其4个特征点位置的弹道倾角分别为11.0°，－11.2°，－22.4°，－32.5°.建立弹丸6自由度运动学模型，数值仿真沿周身分布的单发脉冲修正能力，与式（16）计算结果比较，如图7所示.由此可见式（16）计算结果与6自由度仿真结果一致，验证了式（16）计算方法的正确性.

图7中，由外到内对应于弹道倾角为11.0°、－11.2°、－22.4°、－32.5°的特征点.

图7 脉冲修正矢量图

脉冲修正矢量的计算误差为

6.2 闭环验证

按图3所示组成卫星制导脉冲修正闭环系统，设置无控弹道落点与目标偏差（－235m，100m），采用式（22）设计脉冲发动机点火决策，进行有控弹道仿真.考虑卫星导引头捕星定位时间、卫星导引头量测误差、脉冲发动机冲量摄动、弹体滚转相位测量误差以及风偏等相关扰动因素进行仿真计算.要求Ecp≤12m，仿真结果平均脱靶量为（－7.52m，－3.50m），在Ecp要求的范围之内，从而验证了本文研究的卫星制导炮弹脉冲修正矢量计算方法的有效性.

通过6自由度弹道仿真和控制系统闭环验证，充分说明了卫星制导炮弹脉冲修正矢量计算方法的正确性和有效性，可以为脉冲发动机设计和控制决策系统研究提供较好的参考价值.

[1]HABLANI H B.Pulsed guidance of exoatmospheric interceptors with image processing delays in angle measurements，AIAA 2000－4272[R].2000.

[2]王中原，丁松滨，王良明.脉冲修正弹在脉冲力矩作用下的飞行稳定性条件[J].南京理工大学学报，2000，24（4）：322－325.WANG Zhong－yuan，DING Song－bin，WANG Liang－ming.Flight stability condition for a projectile of corrected trajectory with impulse moments[J].Journal of Nanjing University of Science and Technology，2000，24（4）：322－325.（in Chinese）

[3]寇保华，张晓今，杨涛，等.脉冲式末制导子弹导引规律的研究[J].弹道学报，2005，17（1）：28－31.KOU Bao－hua，ZHANG Xiao－jin，YANG Tao，et al.Study of guidance law for impulse terminal guidance sub－munitions[J].Journal of Ballistics，2005，17（1）：28－31.（in Chinese）

[4]徐劲祥.末段修正迫弹脉冲修正方案研究[J].弹箭与制导学报，2005，25（1）：50－52.XU Jin－xiang.A study on impulse correction scheme of terminal correction mortar projectile[J].Journal of Projectiles，Rockets，Missiles and Guidance，2005，25（1）：50－52.（in Chinese）

[5]钱杏芳，林瑞雄，赵亚男.导弹飞行力学[M].北京：北京理工大学出版社，2008.QIAN Xing－fang，LIN Rui－xiong，ZHAO Ya－nan.Missile flight mechanics[M].Beijing：Beijing Institute of Technology Press，2008.（in Chinese）