复合控制空空导弹大机动控制律设计及仿真

侯满义，解增辉，范惠林

（1.空军航空大学 航空军械工程系，长春130022；2.中国人民解放军93802部队，陕西 咸阳712200）

采用直接力/气动力复合控制可以使导弹快速实现大攻角飞行和大角速率操纵，大大提高了可用过载，增强了机动能力.但是当导弹进行大攻角飞行时，其气动力和力矩将呈现明显的非线性和不确定性，且气流出现强不对称性，这致使控制通道严重耦合.此时，传统的控制方法不再适用，必须设计新的控制器.

对于非线性导弹系统，在很多文献中研究设计了非线性控制器，但主要是针对BTT导弹[1～5].而对于复合控制空空导弹，只有在越肩发射或末制导情况下才可能启动直接力控制进行大攻角机动，其大部分飞行时段仍应用常规控制器.基于此，考虑先将非线性耦合系统转换为线性的解耦系统，然后再设计控制器，以匹配原有的常规控制.

应用微分几何理论实现反馈线性化是一种重要的非线性控制方法，对于耦合不确定多变量非线性系统，在实现线性化的同时还可以实现解耦，这正是研究所需要的.但反馈线性化方法依赖系统精确的非线性模型，对建模误差敏感，为解决这一问题，出现了鲁棒反馈线性化方法，将其与神经网络控制[6]、变结构控制[7～9]或H∞控制[10]相结合，但它们只考虑了线性化后的系统干扰，没有研究原非线性系统干扰的可能情况或匹配条件.本文从具有干扰的非线性系统出发，对于复合控制空空导弹，设计了基于反馈线性化的RBF神经网络变结构控制器，并通过仿真说明了方法的有效性.

1 弹体姿态运动数学模型

复合控制空空导弹在进行大攻角机动时，各控制通道间主要存在惯性和动力学耦合作用[2]，在一定简化处理后，滚转通道可独立出来进行单通道控制律设计.本文主要研究俯仰/偏航两通道的解耦控制问题，为便于分析，设发动机推力沿弹体纵轴方向，弹体惯性积为0，建立数学模型为

式中，Fp、Fy、Fz、G、Mz、My分别为作用在导弹上的推力、升力、侧力、重力、俯仰力矩和偏航力矩，α、β、θ、γV分别为导弹飞行攻角、侧滑角、弹道倾角和倾斜角，ωx、ωy、ωz为弹体滚转角速度、偏航角速度和俯仰角速度，Jx、Jy、Jz为转动惯量，m和v为导弹质量和速度.其中，Fy、Fz的力系数Cy、Cz和力矩My、Mz的表达式为

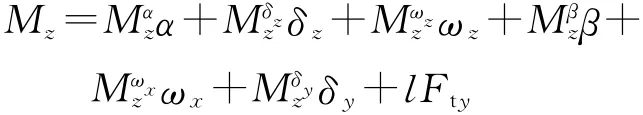
式中，δy、δz分别为偏航舵偏角、俯仰舵偏角，Cαy为攻角引起的升力变化曲线的斜率，Cβz为侧滑角引起的侧力变化曲线的斜率，Mωxy为滚转角速度引起的偏航力矩变化曲线斜率，Mδyz为偏航舵偏角引起的俯仰力矩变化曲线斜率，Fty、Ftz分别为直接力沿弹体坐标系y轴和z轴方向上的分量，l为直接力作用点与导弹质心之间的距离.

可以看出，这是一个四输入（俯仰、偏航方向的舵偏和直接力）双输出（攻角和侧滑角）的非线性耦合系统，导弹在大姿态角机动时，这种非线性和耦合作用不容忽略.

2 反馈线性化解耦

式中，

假设直接力控制的推力矩lFt可连续线性变化，即：

式中，Mmax为最大可用直接推力矩，δjet为直接力控制的等效舵偏控制量，则导弹俯仰和偏航方向的直接力控制存在控制量δzjet和δyjet，它们可映射为与气动控制舵偏δz和δy具有相同意义的虚拟控制量，这样复合控制导弹系统就成为一个双输入双输出耦合系统，本文统一用δz和δy表示控制量.

将反馈线性化方法应用于复合控制空空导弹的姿态控制中，选择导弹系统的输出变量Y＝（αβ）T，输入控制变量U＝（δzδy）T，状态变量X＝（αωzβωy）T.由于控制舵面所产生的升力和侧力属于小量，因此只考虑舵偏对力矩的影响，令Cδyz＝Cδzy＝0，同时令sinγV≈γV，cosγV≈1，则控制系统的状态空间描述为

f（X）、N（X）、H（X）均为光滑向量场，Mmax为最大可用直接推力矩，d（t，X）为系统的不确定干扰或未建模部分，这是控制器设计所要考虑的重点，要实现系统的反馈线性化解耦，d（t，X）需满足下列匹配条件和有界条件，证明略[3].

式中，dM为未知干扰上界，为已知量.

对于非线性系统（3），应用微分几何理论，分别求标量函数h1（X）、h2（X）对向量场f（X）和g1（X）、g2（X）的李导数，有：

同理得Ldh1＝Ldh2＝0，LdLfh1≠0及LdLfh2≠0.系统相对阶向量（r1r2）＝（2 2），不存在零动态子系统，则系统Falb－Wolovich矩阵为

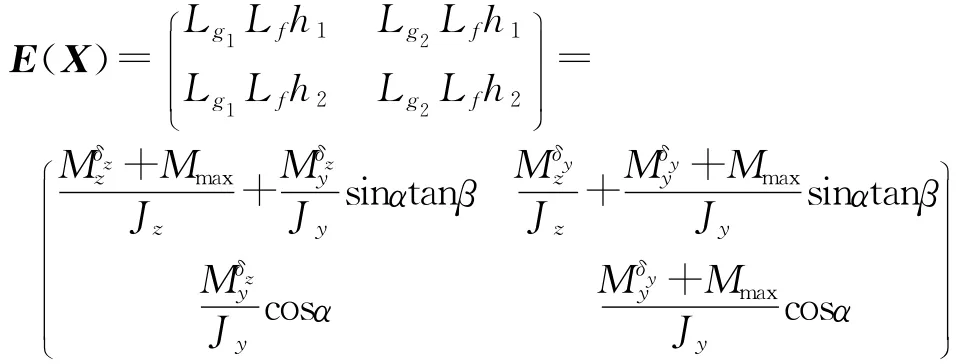
矩阵E（X）非奇异，构造如下微分同胚映射，进行非线性状态变换.

取状态反馈控制律：

V＝（V1V2）T为输入变量，则系统状态空间方程变为

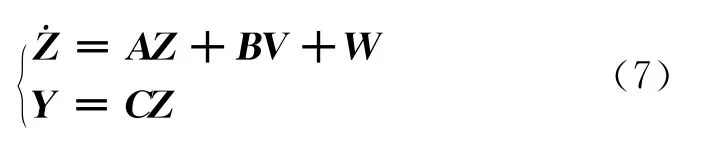
式中，

至此，通过反馈线性化将非线性系统映射到线性空间，状态空间拓扑结构保持不变，导弹的俯仰/偏航控制已被解耦成2个独立的控制子系统，干扰也实现解耦.针对每个控制通道，设计RBF网络变结构控制器.

3 滑模变结构控制器设计

一定条件下，滑动模对于干扰与参数的变化具有不变性，这正是鲁棒性控制要解决的问题，利用此优点来设计变结构控制器不失为一种很好的鲁棒控制方法.

3.1 切换流形设计

考虑跟踪问题，设Ydi为参考输入，Yi为实际输出，ei＝Ydi－Yi为跟踪误差，第i个通道（i＝1，2）的切换函数为

方程Si（ei）＝0即为切换流形，其中＝di－Lfhi（X），（A，B）可控，则滑动模态可控，滑动运动的性能品质取决于参数ci的值.

3.2 控制律设计

设计了切换流形，再设计变结构控制律，使系统在任一初始状态都能于有限时间内到达切换流形，并具有良好的品质性能，进而实现滑动模运动.本文采用趋近律方法设计控制器，选取指数趋近律：

式中，ki、λi为大于0的常数.当导弹控制系统中的不确定干扰满足式（4）时，有：

由式（10）可知，当ki＞dM时，Sii＜0，状态可达切换流形，其运动品质可通过选取ki和λi进行调节.

由式（8）、式（9）得变结构控制：

为了削弱控制抖振，用连续函数Si/（｜Si｜＋ε）代替符号函数sgn（Si），ε为消颤因子.式（11）变为

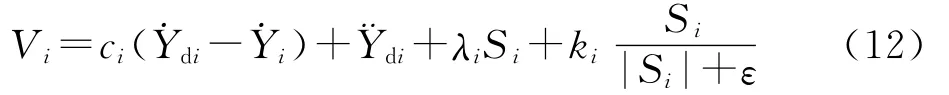
代入式（6），即可计算出反馈控制律U.由于实际系统切换装置存在惯性，加上各种滞后与未建模动力学因素的影响，系统控制容易产生剧烈抖振.由式（11）可知，控制器抖振与切换项ki有密切关系，ki越大，系统克服摄动和干扰的能力就越强，但是增益过大将会导致抖振加大.为此，在ci、λi一定的情况下，通过RBF神经网络实时调节ki，以达到最大抗干扰的同时尽量减小抖振.

设网络输入X1＝（S）T，输出的绝对值ki为

式中，b、q为函数峰值调节项，为常数.

神经网络的权值调节指标为

式中，Δ为误差.

权值学习算法为

式中，η为网络学习速率，ρ为惯性量系数，t为网络训练样本的时间次序.控制过程中应用系统的实时测量数据对网络进行在线训练.

综上所述，可得复合控制空空导弹的系统控制过程如下图1所示.

图1 反馈线性化神经网络变结构控制结构图

4 仿真分析

设干扰d（t）＝30exp｛－（t－2）2/0.005｝，滚转角速度ωx＝0.1sint，变结构控制中取c1＝c2＝5，λ1＝λ2＝10，ε＝0.02，RBF神经网络选用2－4－1结构，其中η＝0.8，ρ＝0.05.

图2 俯仰跟踪响应

图3 偏航跟踪响应

图2、图3中虚线表示通道控制指令（即系统参考输入），实线表示实际控制输出，可以看出，导弹的俯仰和偏航控制通道实现解耦，系统输出量α、β都能稳定、精确跟踪各自控制指令，说明基于反馈线性化的RBF神经网络变结构控制律能够很好地解决系统耦合（α对俯仰控制、β对偏航控制以及ωx的耦合影响）问题，同时克服了系统干扰d（t）的影响，具有较强的鲁棒性.由于神经网络存在训练过程，所以在跟踪初始阶段有一定偏差，当网络训练完成后，系统跟踪迅速趋于稳定.导弹俯仰和偏航2个通道的控制量变化如图4所示.

控制过程中如果k取为固定值k1＝k2＝1.5，则在相同指令跟踪效果下，控制量变化如图5所示.

对比可以看出，通过应用RBF神经网络对变结构控制器中的k值进行实时调节，在保证系统稳定跟踪的同时，还可以大大削弱控制量的抖振.

图4 k实时调节时俯仰和偏航控制量的变化曲线

图5 k取固定值时俯仰和偏航控制量变化曲线

5 结束语

针对直接力/气动力复合控制空空导弹系统存在的时变非线性强耦合特性，本文通过适当的假设转换，基于反馈线性化方法实现了控制通道的解耦，并设计了RBF神经网络变结构控制器.仿真结果表明导弹俯仰和偏航通道都能稳定跟踪控制指令，鲁棒性较强，且控制量抖振得到有效抑制.可以看出，基于反馈线性化的变结构控制方法使得复杂的导弹控制系统设计问题大大简化，但是在实际应用过程中，要求干扰d（t）有界匹配往往比较难做到，这些问题还有待进一步研究.

[1]张友安，胡云安.导弹控制和制导的非线性设计方法[M].北京：国防工业出版社，2003.ZHANG You－an，HU Yun－an.Nonlinear design approaches for missile control and guidance[M].Beijing：National Defense Industry Press，2003.（in Chinese）

[2]李言俊，张科.自适应控制理论及应用[M].西安：西北工业大学出版社，2005.LI Yan－jun，ZHANG Ke.Adaptive control theory and applications[M].Xi’an：Northwestern Polytechnical University Press，2005.（in Chinese）

[3]胡跃明.非线性控制系统理论与应用[M].北京：国防工业出版社，2001.HU Yue－ming.Nonlinear control system theory and applications[M].Beijing：National Defense Industry Press，2001.（in Chinese）

[4]ZHU W Q，YING Z G，SONG T T.An optimal nonlinear feedback control strategy for randomly excited structral systems[J].Nonlinear Dynamics，2001，24（1）：31－51.

[5]夏小华，高为炳.非线性系统控制及解耦[M].北京：科学出版社，1993.XIA Xiao－hua，GAO Wei－bing.Nonlinear system control and decoupling[M].Beijing：Science Press，1993.（in Chinese）

[6]王庆超，李达.基于反馈线性化的动能拦截器姿态控制研究[J].宇航学报，2005，26（3）：358－361.WANG Qing－chao，LI Da.A study of kinetic interceptor attitude control system based on feedback linearization[J].Journal of Astronautics，2005，26（3）：358－361.（in Chinese）

[7]韩艳铧，周凤岐，周军.基于反馈线性化和变结构控制的飞行器姿态控制系统设计[J].宇航学报，2004，25（6）：637－641.HAN Yan－hua，ZHOU Feng－qi，ZHOU Jun.Design for aerocraft attitude control system based on feedback－linearization and variable－structure－control[J].Journal of Astronautics，2004，25（6）：637－641.（in Chinese）

[8]SINGH S N，IYER A.Nonlinear decoupling sliding mode control and attitude control of spacecraft[J].IEEE Transactions on Aerospace and Electronic System，1989，25（5）：621－633.

[9]闫海波，郭科，王茂芝，等.基于反馈线性化和变结构控制的速度饱和伺服系统设计[J].宇航学报，2006，27（4）：616－619.YAN Hai－bo，GUO Ke，WANG Mao－zhi，et al.The design of velocity saturation servo system based on feedback－linearization and variable structure control[J].Journal of Astronautics，2006，27（4）：616－619.（in Chinese）

[10]胡跃明.变结构控制理论与应用[M].北京：科学出版社，2003.HU Yue－ming.Variable structure control theory and application[M].Beijing：Science Press，1993.（in Chinese）