一种Terminal滑模制导规律研究

张 旭，雷虎民，曾 华，朱良志

（1.空军工程大学 导弹学院，陕西 三原713800；2.中国人民解放军94211部队，河南 商丘476000）

随着空间技术的发展，弹道导弹、空间飞行器等空中目标的机动突防能力越来越强，对各国安全构成了严重的威胁[1，2].基于滑模变结构控制理论的滑模变结构制导律因其设计简单、易于工程实现，同时具有对外界干扰和系统不确定性的鲁棒性，成为制导律研究的热点.但是，目前大多数变结构制导律一般选用线性滑模面，无论如何，状态跟踪误差都不会在有限时间内收敛到0，不能很好地适用于动能拦截器“趋零脱靶量”精确制导能力的要求[3]，因此，迫切需要研究使视线角速率在有限时间内收敛到0的高精度制导律.

近年来，为了解决视线角速率快速收敛到0的问题，一些学者提出了Terminal滑模控制策略[4，5]，即在滑动超平面的设计中引入了非线性函数，构造非线性Terminal滑模面，使得在滑模面上跟踪误差能够在有限时间内收敛到0.

文献[6]设计了一种基于零控拦截的EKV末段制导律，在对常规弹道类目标进行逆轨拦截时能够取得较好的效果，但是对于大机动目标，其所设计的扩展比例导引律就会产生很大的脱靶量.文献[7]提出了制导系统有限时间收敛的充分条件和一种形式简洁的有限时间收敛变结构导引规律，但是该导引律只能保证视线角速率在末制导结束前收敛到0，不能使视线角速率在末制导开始后短时间内收敛到0.

针对高速度、大机动目标，本文将Terminal滑模控制策略引入到制导律设计中，通过构造非线性滑模超平面，设计了一种能够使视线角速率在末制导开始后短时间内收敛到0的高性能制导律，并与比例导引法、经典变结构制导律、全局Terminal滑模制导律进行了详细的分析比较，说明了所设计制导律的优越性能.

1 导引段的相对运动方程

拦截器与目标的相对运动如图1所示，图中，IxI、IyI、IzI为平行于惯性参考坐标系的三个坐标轴方向；T为目标，IT为视线，r为导弹与目标的相对距离，IxLyLzL为视线坐标系，θL为视线倾角，φL为视线偏角，θI和φI分别为拦截器的弹道倾角和弹道偏角，θT和φT分别为目标的弹道倾角和弹道偏角.

图1 拦截器－目标运动学关系

为了研究导引规律，末制导过程中的相对运动可以解耦成纵向平面IxLyL内的运动和侧向平面IxLzL内的运动.在某一时间区间 Δt内，ΔxL、ΔyL、ΔzL分别为xL、yL、zL的增量.

本文主要针对动能拦截器纵向平面内的制导律进行研究，故给出纵向平面内的相对运动学方程.设在Δt内，视线倾角的增量为ΔθL，则

式中，r（t）为动能拦截器与目标在纵向平面内的相对距离，ΔyL（t）为 Δt时间内IyL方向上的相对位移.若时间区间Δt足够小，则ΔθL（t）是一个很小的量.因此有：

将式（2）对时间t进行微分，可得：

把 ΔyL（t）＝r（t）ΔθL（t）代入式（3），可得：

把式（4）等号两边对时间t再微分一次，可得：

式中，

aIy（t）和aTy（t）分别为动能拦截器和目标机动加速度在IyL方向上的分量.

为了便于设计制导律，取状态变量x1＝ΔθL（t），，那么由式（7）可得纵向平面内相对运动的状态方程为

干扰量为

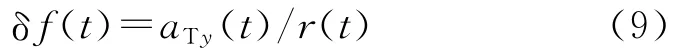
设D（t）为干扰量的界，则｜δf（t）｜≤D（t）.

2 基于Terminal滑模的制导律设计

2.1 非线性滑模超平面设计

设期望状态Xd＝（x1dx2d）T＝（x1d1d）T，通过设计Terminal滑模控制律，使系统状态X＝（x1x2）T在有限时间内实现对期望状态Xd的跟踪.

定义误差向量为

式中，e＝x1－x1d.由于在制导律设计过程中，期望ΔθL（t）和（t）趋向于0，故选取Xd＝（0 0）T，则

非线性滑模面方程设计为

式中，C＝（C1C2），C1、C2为正的常数；W（t）＝CP（t），P（t）＝ （p（t）（t））T，p（t）满足如下假设：p（t）：R＋→R，p（t）∈Cn[0，∞），p（t）、（t）∈L∞.对于某个常数T＞0，p（t）是在时间段[0，T]上有界的，并且p（0）＝e（0）（0）＝（0）.Cn[0，∞）表示定义在[0，∞）上的所有二阶可微连续函数.

选取非线性函数p（t）为

式中，参数ajl可通过上述假设中的条件获得.

2.2 制导律设计及稳定性证明

式（12）对t求微分，可得：

将式（8）、式（11）代入式（14），可得：

设计Lyapunov函数为

令u＝aIy，对上式进行微分，可得：

为使式（17）的取值小于0，可将制导律设计为

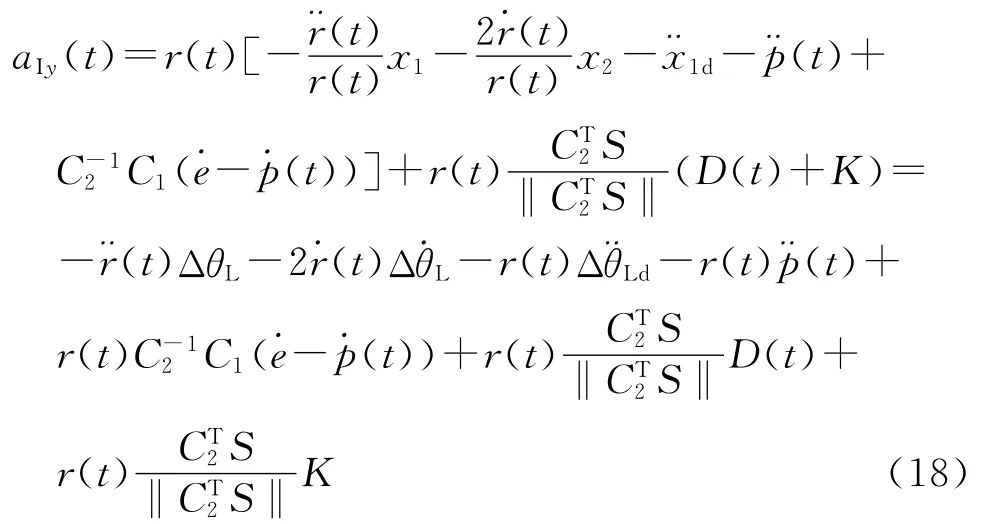
式中，K为正的常数.

将式（18）代入，可得：

从而证明了所设计的控制系统是全局渐近稳定的.

根据p（t）满足的条件和 Terminal滑模面方程（12），可得：

即系统的初始状态已经在滑模面上了，消除了滑模控制的到达阶段，确保闭环系统的全局稳定性和鲁棒性.

在末制导过程中（t）变化不大，故（t）≈0；且在实际应用中，干扰δf（t）可能无法得到，考虑变结构控制的鲁棒性，在式（18）中将干扰项略去；令，从而得到简化的制导律为

由于系统具有全局鲁棒性，即S（X，t）＝0或E（t）＝P（t）.故通过选择 Terminal滑模面中的函数P（t）＝（00）T，实现E（t）＝（00）T，从而保证跟踪误差在有限时间T内收敛至0.

2.3 基于准滑模控制的Terminal滑模制导设律计

抖振问题是影响滑动模态控制广泛应用的主要障碍，引起抖振的根本原因在于开关函数的不连续性，为此本文将继电特性连续化的方法引入到制导律设计当中，即在边界层外采用正常的滑模控制，在边界层内采用连续状态反馈控制，从而避免或削弱抖振的影响，实现了准滑动模态控制.

在式（22）中，用连续函数Θ（S）代替符号函数sgn（S）.Θ（S）的表达式为

2.4 非线性函数p（t）及其导数的计算公式推导

根据式（13），p（t）可写为

式中，δ0、δ1为很小的正数.

由式（22）和式（23）可得纵向平面内的Terminal滑模制导律为

p（t）的一阶导数和二阶导数可通过对式（25）分别求一阶导数和二阶导数得到.

根据p（t）满足的条件，可知，当t＝T时，p（t）＝0；将其代入式（25），经化简，可得：

由于e（0）、（0）、（0）不恒为0，则p（T）＝0成立的必要条件为

同理，由t＝T时（t）＝0，得（t）＝0的必要条件为

解方程组（27）～方程组（29）可得p（t）的系数矩阵，将其代入式（13），可得p（t）的表达式为

3 仿真结果分析

以动能拦截器大气层外拦截为例，两飞行器在惯性坐标系下进入末制导时的状态参数：拦截器的位置为（0，9.5km），初始弹道倾角为0.034 9rad，速度为2 000m/s；目标的位置为（35km，10km），初始弹道倾角为3.141 6rad，速度为2 500m/s.

在本文的空间拦截实例仿真中，导弹的最大允许过载为3g，不考虑拦截器的控制系统延迟；导引头的采样周期和指令形成周期在开始拦截时为10ms，当拦截器和目标的距离小于300m时，改为1ms，这样既保证了仿真速度，又保证了拦截精度；拦截器的制导盲区设置为100 m，即当拦截器与目标的距离小于该距离时，轨控发动机关机，制导指令为0，拦截器依靠惯性向目标飞去；目标为逃避拦截做沿着飞行弹道法向的正弦加速机动：

式中，aTmax为目标最大机动加速度.TVSG的参数取值为C＝（5 1）T，K＝2，δ0＝0.01，δ1＝2.0，T＝0.1s.

在仿真中还将Terminal滑模制导律（TVSG）的仿真结果与真比例导引（TPN）、经典滑模制导律（CVSG）、全局 Terminal滑模制导律（GTVSG）进行比较.

其中，TPN的形式为

式中，导引系数N＝3.

CVSG的形式如下：

式中，k＝2，ε＝10，δ＝0.001.

GTVSG 的形式[8]如下：

式中，α0＝2，β0＝0.1，p0＝7，q0＝5，p＝11，q＝9，

考虑拦截过程中动能拦截器为一阶惯性环节，即

式中，aIy为拦截弹指令加速度，aI为拦截弹加速度，τ＝0.01s，s为拉氏变换中的因子.

在拦截器飞行过程中的脱靶量用Δ表示，消耗的能量使用如下公式进行解算：

式中，t0为拦截器发射初始时刻，tf为拦截结束时刻.

仿真结果主要如图2～图5、表1～表3所示.其中，图2～图5是aTmax＝2g情况下的仿真结果，表1～表3为4种制导律在目标机动加速度分别为g、2g、3g时的仿真结果.

图2 弹道轨迹

图3 视线角速率随时间的变化曲线

图4 视线角速率局部放大图

图5 指令加速度随时间的变化曲线

表1 aTmax＝g时的不同制导律的制导性能

表2 aTmax＝2g时的不同制导律的制导性能

表3 aTmax＝3g时的不同制导律的制导性能

由图2及表2可知，当aTmax＝2g时，4种制导律均命中目标，其中TPN和CVSG的脱靶量较大；同时，TPN和CVSG 2种制导律的弹道轨迹明显高于2种Terminal滑模制导律，这主要是由于TPN和CVSG不能使视线角速率快速收敛到0造成的.

图3、图4是4种制导律的视线角速率变化曲线及其局部放大图.由图3可知，TPN的视线角速率在拦截末端迅速发散，这也是导致其脱靶较大的主要原因.由图4的局部放大图可以看出，在整个末制导过程中，TVSG和GTVSG的视线角速率在末制导刚开始就收敛到0并且一直保持不变，直到最后一刻才稍稍增大；而TPN和CVSG从t＝1s时就开始增大，直至最后发散；同时，TVSG的视线角速率比GTVSG能更有效地收敛到0，这是因为GTVSG中缺少与视线角速率收敛时间相关的参数，而TVSG中的非线性函数p（t）包含这个参数，故可以通过对其进行设计来改善视线角速率的趋零特性.Terminal滑模的另外一个重要特点就是在导引的开始阶段指令加速度比较大，之后变得比较小且变化平缓.由图5可知，在前1.8s，TVSG与GTVSG指令加速度较大且趋于饱和，其原因是系统为了使滑模面迅速收敛到0，必须使用较大的控制量.这种制导律的优点是在末制导的初始段，它能够充分利用拦截器的机动能力，使制导律的滑模面快速收敛到0，之后制导指令变得较小，有利于拦截器以较小的脱靶量命中目标；从图5还可知，TPN的指令加速度在最后0.15s达到了饱和，CVSG在最后0.13s也达到了饱和，从而引起了较大的脱靶量.

虽然Terminal滑模在导引初始段制导指令比较大，但其消耗的总能量却比TPN和CVSG少得多.其中TPN和CVSG消耗的能量最多，分别为1 396.040m2/s3和1 281.066m2/s3，而 GTVSG 比较少，为763.465 6m2/s3，TVSG 消耗的能量最少，为751.537 8m2/s3.

由表1～表3可以看出，随着目标机动加速度的不断增大，TPN、CVSG先后出现了脱靶，而GTVSG和TVSG则始终能够以较小的脱靶量命中目标；不仅如此，随着目标机动加速度的不断增大，4种制导律的拦截时间和能量消耗也有所增加，但GTVSG和TVSG一直保持在比较低的状态.然而，无论目标以何种加速度逃逸，TVSG总能够以最小的脱靶量、最少的拦截时间和能量消耗命中目标.

4 结束语

本文针对动能拦截器拦截空间高速度、大机动目标的问题，结合其可用过载小、燃料受限、对脱靶量要求高等特点，基于Terminal滑模控制策略，构造Terminal滑模超平面，设计了纵向平面内的Terminal滑模制导律.该制导律可以使视线角速率在有限时间内趋向于0，从而保证了其较小的脱靶量、拦截时间、能量消耗和鲁棒性.通过与比例导引法和经典变结构制导律进行对比，说明Terminal滑模制导律的优越特性；由于全局Terminal滑模制导律与本文所设计的Terminal制导律均是基于有限时间收敛的思想，因此，二者在制导性能上有一些相似之处，但是通过仿真分析可以发现，本文所设计的Terminal滑模制导律具有更好的制导性能.

由于在制导律设计时忽略了拦截器姿态控制系统的误差和延迟、轨控发动机的推力特性以及制导信息的获取等因素，因此，在制导律设计时考虑拦截器的姿轨控特性以及制导信息的获取方法将是下一步研究的主要方向.

[1]康兴无，陈刚.天对地精确攻击武器末段制导律设计[J].固体火箭技术，2009，32（1）：11－14.KANG Xing－wu，CHEN Gang.A terminal guidance law design applied to space－to－surface precision attack weapons[J].Journal of Solid Rocket Technology，2009，32（1）：11－14.（in Chinese）

[2]赵吉松，谷良贤，龚春林.高超声速跳跃－滑翔弹道方案设计及优化[J].固体火箭技术，2009，32（2）：123－126.ZHAO Ji－song，GU Liang－xian，GONG Chun－lin.Design and optimization of hypersonic skip－glide trajectory[J].Journal of Solid Rocket Technology，2009，32（2）：123－126.（in Chinese）

[3]ZHOU D，SUN S，TEO H L.Guidance laws with finite time convergence[J].Journal of Guidance，Control，and Dynamics，2009，32（5）：1 838－1 846.

[4]FANG Y，YU X H.Non－singular terminal sliding mode control of rigid manipulators[J].Automatica，2002，38：2 159－2 167.

[5]YU S H，YU X H，MAN Z H.Robust global terminal sliding mode control of SISO nolinear uncertain system[C].Proceedings of 39th IEEE Conference on Decision and Control.Sydney，Australia：IEEE，2000：2 198－2 203.

[6]冯杰，鲜勇，刘顺成，等.基于零控拦截的EKV末段拦截弹道仿真[J].飞行力学，2010，28（2）：75－81.FENG Jie，XIAN Yong，LIU Shun－cheng，et al.Trajectory simulation of EKV terminal phase interception based on zero effort[J].Flight Dynamics，2010，28（2）：75－81.（in Chinese）

[7]孙胜，周荻.有限时间收敛变结构导引律[J].宇航学报，2008，29（4）：1 258－1 262.SUN Sheng，ZHOU Di.A finite time convergent variable structure guidance law[J].Journal of Astronautics，2008，29（4）：1 258－1 262.（in Chinese）

[8]汤一华，陈士橹，徐敏，等.基于Terminal滑模的动能拦截器末制导律研究[J].空军工程大学学报，2007，8（2）：22－25.TANG Yi－hua，CHEN Shi－lu，XU Min，et al.Terminal guidance law of kinetic interceptor based on terminal sliding mode[J].Journal of Air Force Engineering University，2007，8（2）：22－25.（in Chinese）