中国上市公司动态违约概率研究——基于KMV模型的实证检验

李裕丰， 李 倩， 于 洋

(沈阳工业大学 经济学院， 沈阳 110870)

中国大型商业银行即将在2010年底实施新巴塞尔协议，各家进入试点的商业银行都根据自身业务特点建设起全新的信用风险管理体系。但是，我国目前的金融体系相对不完整，金融市场尚未完善，不能完全照搬国际上广泛使用的几种信用风险管理办法，而需要对信用风险管理的核心变量——违约概率的测算方法进行深入研究，使其理论假设和参数设定适合中国特定的金融环境，这在美国金融危机爆发并引起金融监管变革的背景下具有重要而紧迫的现实意义。

本文以KMV模型作为研究框架，以该模型计算出的上市公司预期违约概率作为最终的输出变量。该模型由布莱克(Black)、斯科尔斯(Scholes)和默顿(Merton)开发的期权定价模型衍生而来，它创造性地将期权定价理论应用于分析评估公司的信用风险，其基本思想是把公司股权看作以资产的市场价值为标的资产、负债的账面价值为执行价格、负债的到期日为执行日期的看涨期权，认为资产结构与公司价值密切相关，而违约概率是与债务额和债务人公司资产结构相关的内生变量。在这种基本思想下，KMV模型假定公司的某种负债水平为期权的执行价格，当公司资产价值低于这个负债水平时就会发生违约。同时，KMV模型又假设投资组合是高度分散的，市场利率和总体经济状况是可以预先确定的，在一定时间里公司的债务结构是固定不变的。这样，这个被假定为期权执行价格的负债水平被定义为违约点(default point，DP)，违约的可能性可以被定义为公司资产价值小于违约点的概率[1]。由此，公司资产价值和违约点就是计算公司违约概率的两个重要变量。

从国内外的研究情况来看，由于KMV公司并未公布该模型的核心函数，国外研究主要体现在早期理论思想的阐述上，而国内研究大多是介绍引进该模型并试图将其应用于中国的信用风险评估。鲁炜(2003)等介绍了KMV模型的构造原理，并试图破解其核心函数关系；陈东平(2007)等通过引入银行不良贷款率作为违约率的替代变量对KMV模型进行了修正。这些研究的不足之处在于，它们都采用比较静态的分析方法，通过计算特定区间的标准差来得出违约概率。本文在前人研究的基础上，通过GARCH方法求出违约距离和理论违约概率的连续时间序列，将计算结果动态化、图形化，并以2007—2009年上市公司数据为样本，分析美国金融危机期间中国上市公司信用风险的连续变化，从而真正把KMV模型作为前瞻性风险管理方法的优势表现出来，同时也检验了KMV模型在中国市场的适用性。

一、模型构建

首先，根据B-S模型，可以得到在到期日T时公司资产市场价值与公司负债账面价值(也就是期权的执行价格)之间的关系[2]，如式(1)所示：

S=Call=VN(d1)-Ke-rτN(d2)

(1)

式中：S——股权的市场价值；

V——公司资产的市场价值；

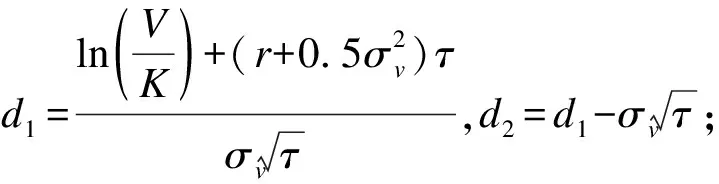
K——负债的账面价值，即执行价格；

r——无风险利率；

τ——距离到期剩余的时间，τ=T-t。

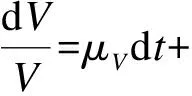
(2)

式中：ηSV——股权价值对公司资产价值的弹性；

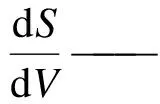
由于欧式看涨期权的Delta值为N(d1)，可以得到

(3)

从式(1)和式(3)可以看出，所有变量中S，σS，K和τ均为已知，通过联立这两个方程，可以解出两个未知数V和σV。这里应该注意的是：对于式(1)来说，期权定价理论是其建立公司价值及其隐含波动率之间函数的理论基础，已经被理论和实务界广泛认可；但式(3)中所设定的公司资产波动性与公司股票价值波动性都服从相同随机过程的理论假设则存在一定争议，而穆迪公司也并未公开其实际使用的函数[4]，这里仅从KMV理论模型的角度进行研究。

另外，为进行迭代运算，不能简单计算一组数据的标准差来代表其波动状况，而需要运用GARCH模型估计时间序列数据的条件标准差。大量实证分析表明，用GARCH(1，1)或GARCH(1，2)模型都能够很好地解释条件异方差[5]184-185。本文将GARCH(1，1)推广到GARCH(1，2)，从而适当地描述波动的聚类性，可以更好地检验KMV模型的敏感度。因此，采用下述条件均值和条件方差方程，得出公司股价收益率条件方差的时间序列[6]287-293，即

rt=C+AR(1)rt-1+AR(2)rt-2+εt-MA(1)εt-1

μt=εt-MA(1)εt-1

按照经典的期权定价模型对信用风险进行估计，当一个公司资产的市场价值低于其总负债时，就会发生违约。而KMV模型认为该假设是不精确的，这是因为一些长期债务为该公司提供了喘息机会，它假设当公司资产价值低于某个水平时才会发生违约。KMV公司通过对大量违约公司的数据进行分析后得出结论，公司的违约触发点通常位于流动负债与总债务金额之间。因为KMV模型假定公司在一段时间内债务结构保持不变，因此，在实证研究中违约实施点一般等于流动负债加50%的长期负债；同时，KMV模型用资产波动的标准差来衡量标准化公司资产价值与违约点之间的差和公司的违约距离(distance to default，DD)[7]。在模型中，违约距离可以表示为

(4)

数理意义上，违约距离表示为公司价值与违约点的单位绝对距离中含有的资产标准差的数量；但在经济意义上，违约距离代表公司资产价值在风险期限内由当前水平降到违约点的相对距离。违约距离不能明确地显示公司违约风险的大小，需要进一步确定违约距离与违约概率的映射关系，来估计公司的预期违约概率(expected default frequency，EDF)。理论的EDF假定公司价值V服从正态分布，然而正态分布假设在实践中并不合理。实务中，KMV公司采用了经验EDF，运用了大量违约公司样本的历史数据，通过比较违约距离和破产频率的历史数据，确定了违约距离与违约概率的映射关系[8]，即

经验EDF=

限于违约公司数据的不可获得性，这里简单假设公司价值V服从正态分布，并以如下公式计算公司的理论EDF：理论EDF=(1-N(DD))×100%。事实上，对DD和EDF进行估计时所用的参数设定在各种研究中存在不同的解释，而实证检验结果也不尽相同，并且由于对其进行理论修正所需要的工作量巨大，也超出了本文研究的范畴，所以，这里只采用KMV模型最基本的理论函数进行研究。

二、实证研究

首先，关于数据的选取。美国金融危机自2007年发端，并于2008年达到高潮，次年各国的扩张性刺激政策发挥效果，全球经济出现回升态势。为检验美国金融危机对中国上市公司利润的影响，本文通过CCER中国经济金融数据库选取2007—2009年的数据，考察金融危机爆发的整个过程对我国上市公司违约概率造成的影响。考虑到上市公司基本面的不同，分别选取3个绩优股和3个ST股作为样本进行实证研究；同时，考虑到非流通股的问题，样本全部选取已经全流通的上市公司作为研究对象。为避免上市公司分红、配股等因素带来股价异动造成的极端数据，这里采用样本上市公司的每日收盘价的复权价作为计算条件标准差的依据；考虑到股权分置改革已经完成，使用样本公司的总市值作为公司股权价值；同时，为在后面的步骤中更好地检验KMV模型的灵敏度，在不影响拟合准确性的前提下，假设股票收益率的前两期数据都对当期数据产生影响，因此使用GARCH(1，2)来拟合各公司股票收益率的时间序列，适当弱化了波动的聚类特征。

其次，关于无法取得的数据的估计。在KMV理论模型中，违约点一般通过下述公式计算得出：违约点=流动负债+长期负债×0.5，但由于无法掌握上市公司负债的具体变化，流动负债和长期负债均以样本公司的季报数据为准，并假定流动负债和长期负债在当季保持不变并按季调整，与日波动率匹配进行迭代计算。

最后，对时间序列迭代数据的方程求解。利用MATLAB软件，根据Black-Scholes期权定价公式和股票价值波动率σs与资产价值波动率σv之间的函数关系建立两个联立方程，并假设利率r=2.25%，τ=3，代入前两步得出的时间序列数据编制迭代计算程序，反复优化即可得到连续时间变量V和σV的最优解。

由于本文所选取的3年连续时间序列数据量较大，篇幅所限不能列明，这里仅以东风汽车为例进行说明。

第一步，将3年每日复权收盘价输入EXCEL表格后，执行下列MATLAB命令：

load garchdata

DFQC=xlsread(′东风汽车.xls′，′Sheet1′，′D2：D726′)；每日复权收盘价

rate=price2ret(DFQC)

spec=garchset(′m′，1，′p′，1，′q′，2)

spec=garchset(spec，′r′，2)

garchfit(spec，rate)

即可得出该时间序列数据GARCH(1，2)的条件均值和条件方差方程，同时得出条件方差的时间序列，如图1所示。GARCH(1，2)模型的关键参数如表1所示。

图1 条件方差的时间序列

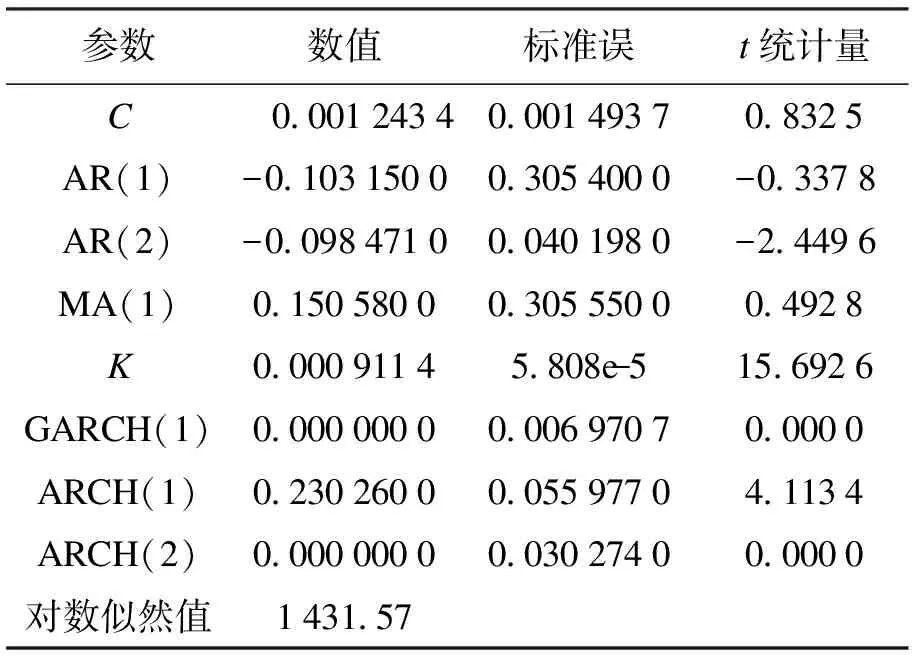
表1 模型的关键参数

第二步，在MATLAB中按照上述模型构建方法设定好KMV模型的求解方程计算程序后，执行下列MATLAB命令计算V和σV以及DD和EDF：

S=xlsread(′东风汽车.xls′，′Sheet1′，′E3：E725′)；%股权价值

K=xlsread(′东风汽车.xls′，′Sheet1′，′K3：K725′)；%违约点

sigs=xlsread(′东风汽车.xls′，′Sheet1′，′L3：L725′)；%股权波动率

for i=1∶723；

a1=S(i)；a2=K(i)；a3=sigs(i)；r=0.0225；

a=fsolve(@(x)myfun(x，a1，a2，a3，r)，[29 000 000 000；0.000 000 1])；

VA(i)=a(1，1)；公司价值最优解

SigA(i)=a(2，1)；公司价值的隐含波动率最优解

end

for i=1：723；

DD(i)=(VA(i)-K(i))/(VA(i)*SigA(i))；违约距离

EDF(i)=normcdf(-DD(i))；理论预期违约概率

end

plot(DD，′DisplayName′，′DD′，′YDataSource′，′DD′)；figure(gcf)

相关上市公司违约距离和理论预期违约概率变化的情况如图2～13所示。

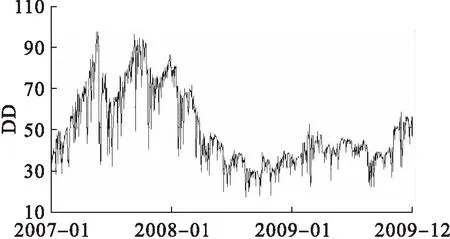
图2 东风汽车(600006)违约距离变化图

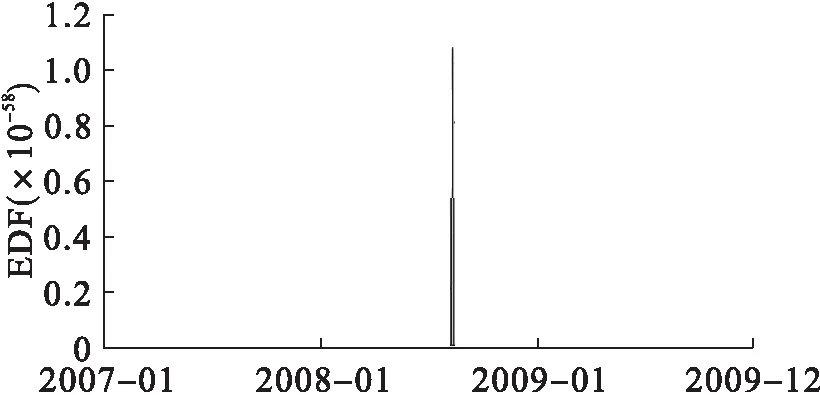
图3 东风汽车(600006)理论预期违约概率变化图

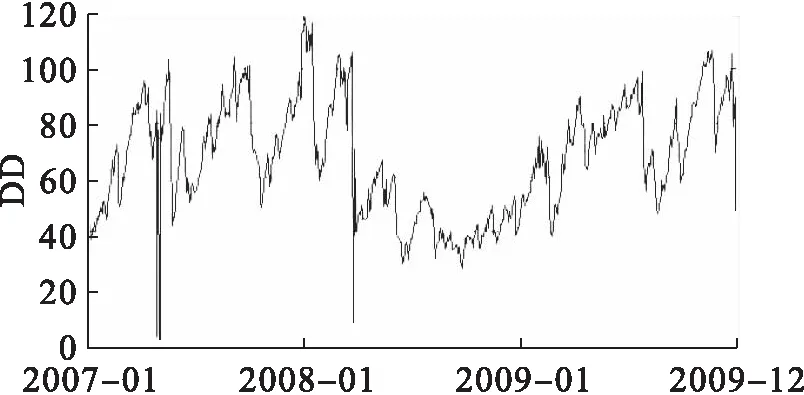
图4 超声电子(000823)违约距离变化图

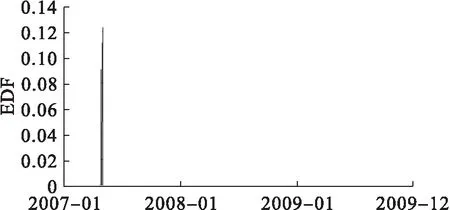
图5 超声电子(000823)理论预期违约概率变化图

第三步，计算时间序列的偏度和峰度，汇总前面DD和EDF以及图中的极大值数据，得到表2。

从上述结果可以看出：

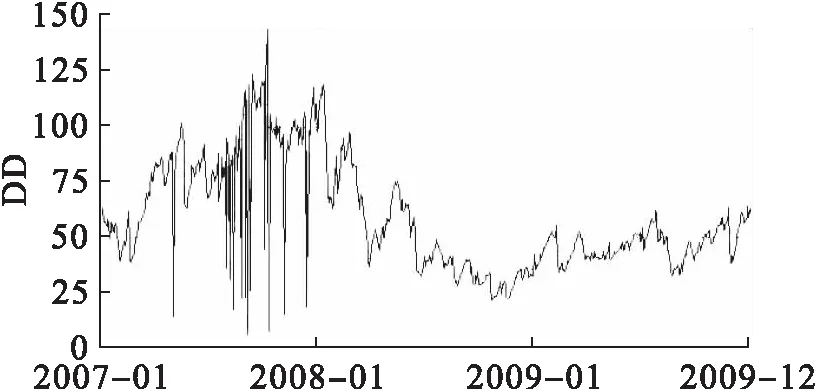
图6 宝钢股份(600019)违约距离变化图

图7 宝钢股份(600019)理论预期违约概率变化图

图8 ST东盛(600771)违约距离变化图

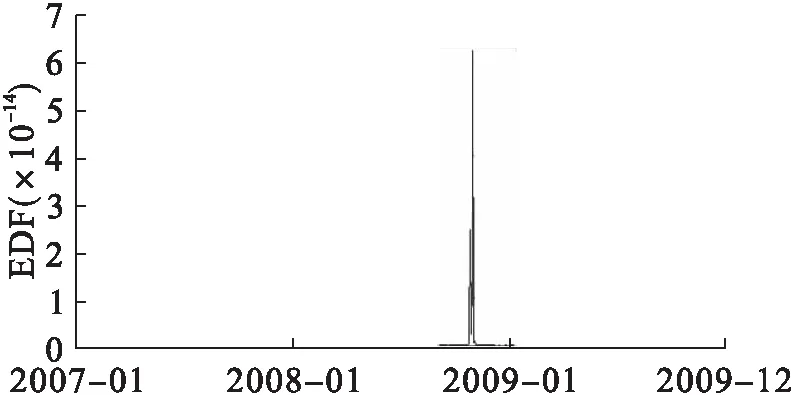
图9 ST东盛(600771)理论预期违约概率变化图

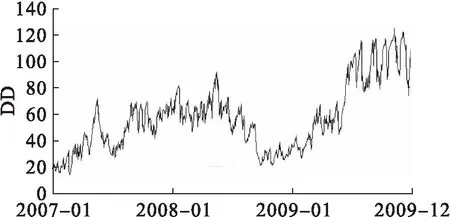
图10 ST达声(000007)违约距离变化图

第一，ST样本公司的公司价值V均存在严重的尖峰、右偏现象，运用理论EDF的正态假设进行估计，可能得到错误的结果。非ST公司资产价值V的正态分布假设比较合理，因此非ST公司的理论EDF解释能力较强。

图11 ST达声(000007)理论预期违约概率变化图

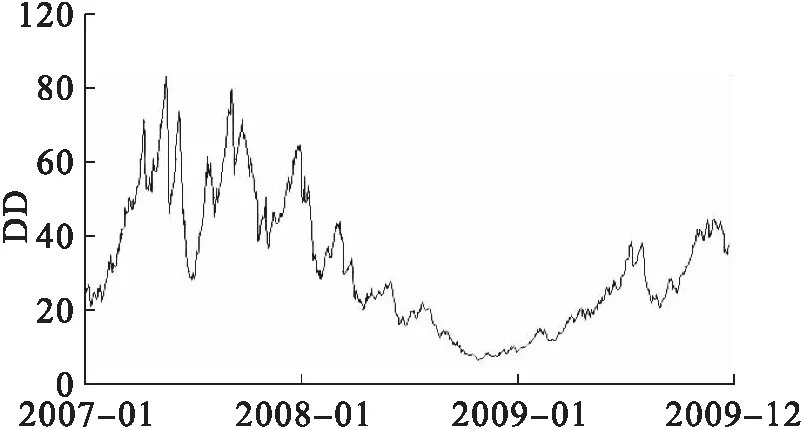
图12 ST昌鱼(600275)违约距离变化图

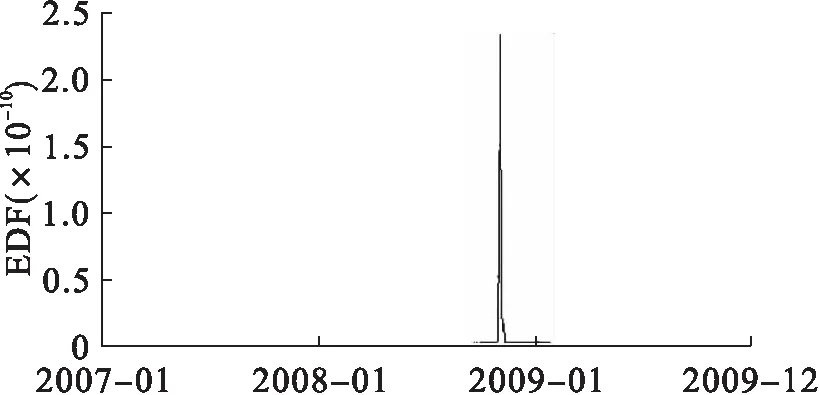
图13 ST昌鱼(600275)理论预期违约概率变化图

第二，表中实证结果的违约概率最大时间点与股价最低时间点存在较强的同步性，说明美国金融危机对中国多数上市公司的违约概率产生了显著影响，而该影响有明显的滞后效应。2007年末美国金融危机爆发，直到2008年末多数上市公司的预期违约概率产生变化，这与2008年底我国经济探底回升的实际情况相符。对于从事不同行业的个别公司来说，出口型公司(如超声电子)违约概率最大值出现在金融危机爆发之前，KMV模型有一定预警作用；而其他公司(如ST达声、宝钢股份)则可能受国内宏观调控等因素的影响，违约概率最大值也早于金融危机发生。

表2 上市公司时间序列数据相关数值

第三，观察各公司的违约概率变化图，可以看出各样本公司理论KMV模型违约距离DD的计算结果表现出较强的同步性，降低了KMV理论模型的实际应用价值。这是由于本文的理论模型对资产价值V、资产波动率σv进行迭代计算时，假设公司价值V服从与股权价值S相同的随机过程，导致资产价值V的波动趋势与股权价值S相同，而实际应用中KMV经验模型采用的关系函数是通过大量历史数据统计得出的[9]。

第四，在本文的实证过程中将该模型应用于个别ST公司时，可能出现得不到最优解的情况，这可能是由于信息的不对称导致的股价数据缺陷造成的。我国A股市场实质上并不存在退市风险，普遍存在的借壳、重组现象，可能造成股价的剧烈震荡，使得ST公司的违约风险很难估计，而且ST公司均存在不确定的资产重组计划，一旦重组成功就会脱胎换骨[10]。

三、结 论

通过KMV模型计算出的动态违约概率基本可以反映出中国上市公司的信用风险状况，但考虑到构建公司价值V与股权价值S的关系函数是影响KMV模型计算结果的主要因素、对于DD和EDF的假设也存在不符合中国实际的情况，因此，着眼于中国应用的KMV模型需要进行适当修正[11]。上述关系函数的建模需要借鉴期权定价之外的其他方法，如通过现金流量折现确定公司价值，违约距离DD和经验EDF的计算则可以通过商业银行的历史数据积累对违约样本公司进行统计得出等。但是，应用KMV模型最大的问题在于我国A股制度上的缺陷使得市场有效性较弱，事实上存在内幕交易等违规行为，使得ST公司的违约概率理论结果失真。只有进一步加强信息披露并完善ST公司的退市制度，才能从根本上解决问题。

参考文献：

[1]Bohn J R.Response to JP Morgan’s paper，“using equities to price credit” [EB/OL].[2001-02-23].http：//www.moodyskmv.com.

[2]Merton R C.On the pricing of corporate debt：the risk structure of interest rates [J].Journal of Finance，1974，29(2)：449-470.

[3]Andrew J，McQuown N A.Comment on market vs accounting-based measures of default risk [EB/OL].[1993-03-15].http：//www.moodyskmv.com.

[4]鲁炜，赵恒珩，刘冀云.KMV模型关系函数推测及其在中国股市的验证 [J].运筹与管理，2003(6)：43-48.

[5]马达拉，拉奥.金融中的统计方法 [M].上海：上海人民出版社，2004.

[6]Philippe J.金融风险管理师手册 [M].张陶伟，译.2版.北京：中国人民大学出版社，2003.

[7]Crosby P J，Bohn J R.Modeling default risk[R].[EB/OL].[2000-01-18].http：//www.moodyskmv.com.

[8]Sellers M V，Oldrich L A.The KMV EDFTMcredit measure and probabilities of default[R].[EB/OL].[2000-05-16].http：//www.moodyskmv.com.

[9]武亦文.KMV模型中资产波动收益率的确定 [J].西南科技大学学报，2008(6)：27-30.

[10]吕长江，赵宇恒.ST公司重组的生存分析 [J].财经问题研究，2007(6)：86-91.

[11]李裕丰.论新巴塞尔协议信用风险框架在中国的适用性 [J].沈阳工业大学学报：社会科学版，2008(3)：226-229.