一般图形与平行线相交之概率＊

蔡定教，鲍旭峰

（安阳师范学院 数学与统计学院，河南 安阳 455002）

一般图形与平行线相交之概率＊

蔡定教，鲍旭峰

（安阳师范学院 数学与统计学院，河南 安阳 455002）

从蒲丰投针问题出发，利用线段与平行线相交之概率，导出一般的凸多边形与平行线相交之概率，进而利用两边夹原理得出一般的凸图形与平行线相交之概率，最后指出一般的图形与平行线相交之概率和其凸包与平行线相交之概率相同．

凸多边形；两边夹原理；凸包

MSC 2000：60D05

0 引言

在1777年出版的《或然性算术实验》一书中，蒲丰提出著名的投针问题，即用实验概率方法计算π．这个实验的操作很简单：找一根粗细均匀、长度为l的细针，并在一张白纸上画上一组间距为a的平行线（方便起见，常取），然后将小针任意投掷在白纸上，这样反复地投多次，数数针与任意平行线相交的次数，就可以得到π的近似值．蒲丰证明了针与任意平行线相交的概率为方法得到圆周率的近似值．在一次实验中，蒲丰选取，然后投针2212次，其中针与平行线相交704次，这样求得圆周率的近似值为2212／704＝3．142．当实验中投的次数相当多时，就可以得到π的更精确的值．

进一步地，我们可以考虑若抛掷的不是一根针而是一个一般的纸片的结果．可以证明在一定条件下任意一个几何图形与平行线相交之概率皆为，这里L为几何图形凸包之周长．下面我们来证明这一结论．

1 几何图形与平行线相交之概率

1．1 线段与平行线相交之概率

平面上画满间距为a的平行直线，向该平面随机投掷一枚长度为l的针（l＜a），试求针与直线相交的概率．这个问题称为蒲丰投针问题，是概率论中的一个著名问题．线段（针）和平行直线相交的概率为p＝

1．2 三角形与平行线相交之概率

平面上画满间距为a的平行直线，向该平面随机投掷一个三边长为l1、l2、l3的三角形硬纸片（l1、l2、l3．利用这一公式，可以用概率＜a），则该三角形与直线相交的概率为做示意图如图1：

易知，只要三角形三边A、B、C中的两条与平行直线相交，三角形与直线就相交，即三角形与直线相交，当且仅当三条边中的两条与平行直线相交．以A、B、C分别表示三角形三边A、B、C与平行线相交之事件，以E表示三角形与直线相交事件．则有：

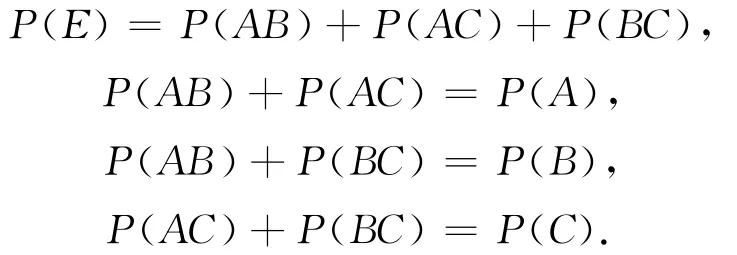
利用线段与平行线相交之概率，不难得到三角形与平行线相交之概率P（E

1．3 凸多边形与平行线相交之概率

平面上画满间距为a的平行直线，向该平面随机投掷一个边长为l1，l2，…，ln的凸多边形纸片（其直径小于a）．做示意图如图2：

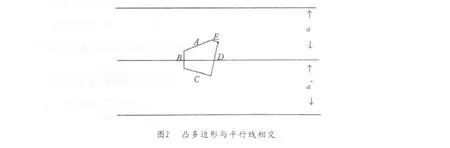
由于是凸多边形，所以其本质和三角形是一样的，只要两条边和平行直线相交就表示图形和平行直线相交．设图形边长为L，即L＝l1＋l2＋…＋ln．由三角形与平行线相交概率的推理方式，可以同理得到凸多边行与平行线相交之概率为

1．4 一般凸图形与平行线相交之概率

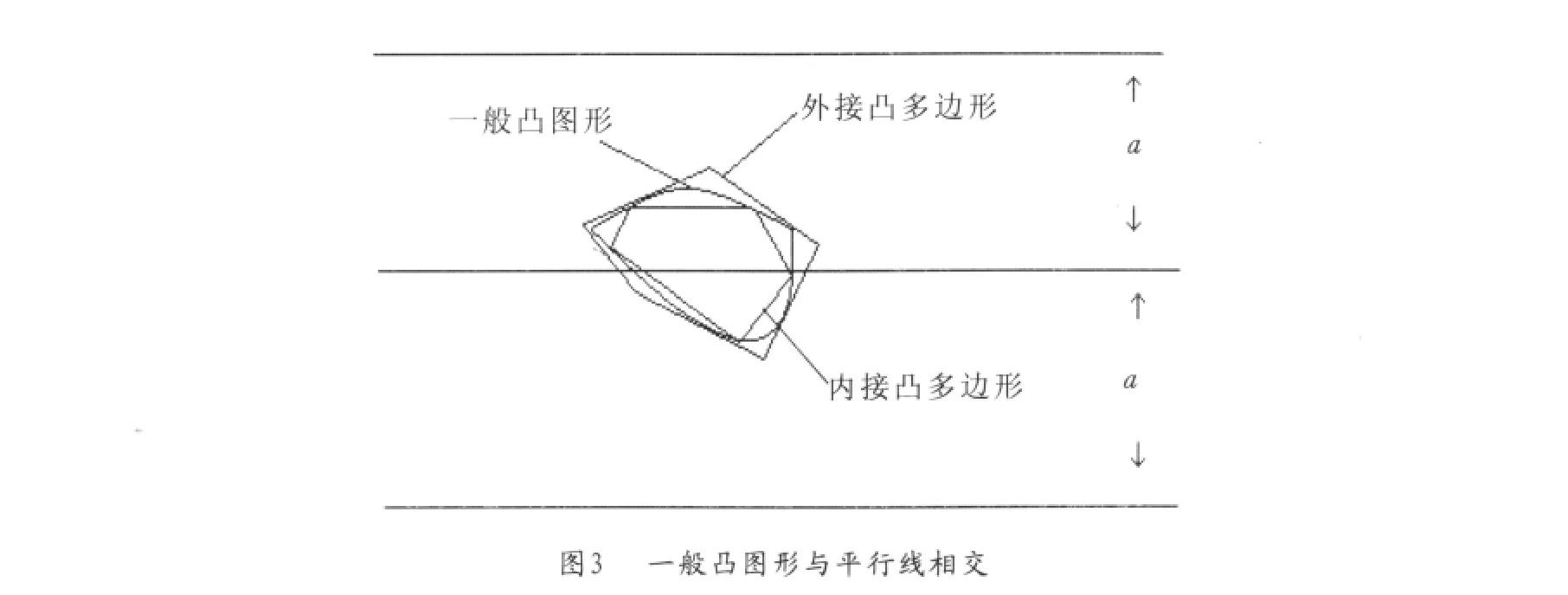
平面上画满间距为a的平行直线，向该平面随机投掷一个一般的凸图形的硬纸片．做示意图如图3．由于是一般凸图形，所以我们很难直接表述它与平行线相交的概率．但我们可以想到一个解决的办法——极限法．如图3画出该图形的一个内接凸多边形和一个外接凸多边形，由于这3个图形都是凸图形，所以明显可以得出：

（1）若内接凸多边形和平行线相交，那么这个一般凸图形也必然和平行线相交；

（2）若一般凸图形和平行线相交，那么外接凸多边形也必然和平行线相交．

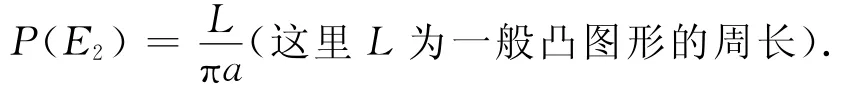
1．5 一般图形与平行线相交之概率

点集Q的凸包（convex hull）是指一个最小凸图形，满足Q中的点在多边形边上或在其内．图4中的多边形就是点集Q＝ ｛p0，p1，…，p12｝的凸包．［3］

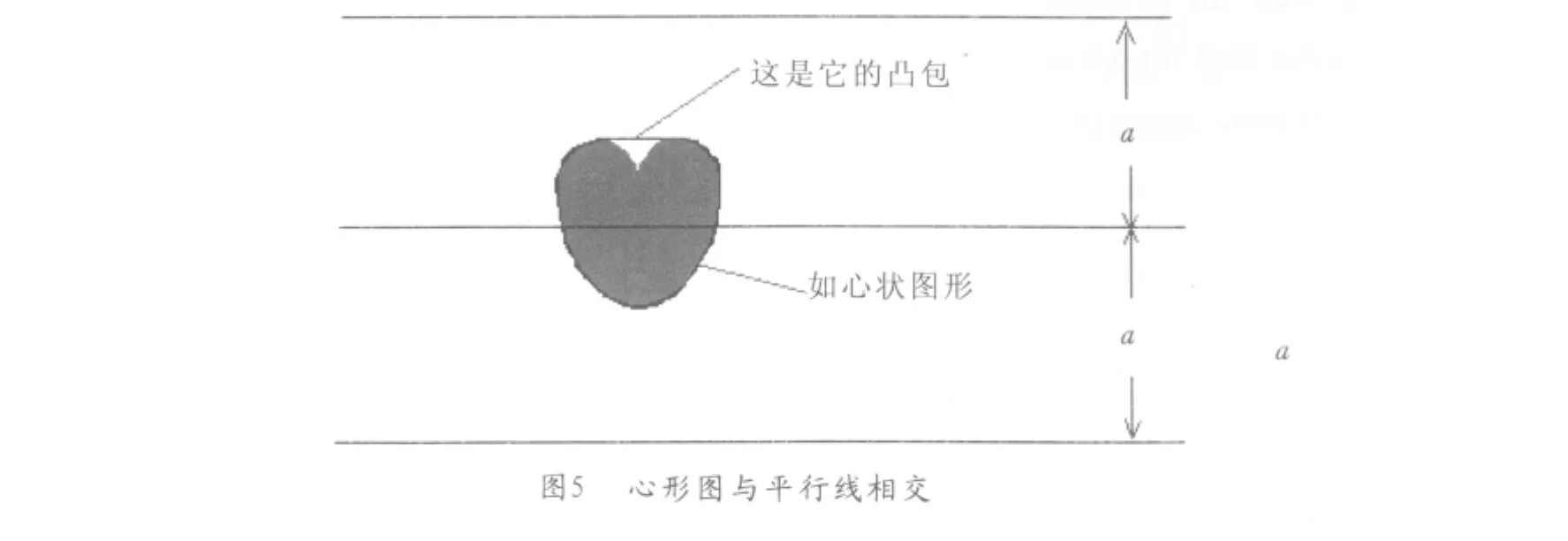
以E1、E2、E3分别表示内接凸多边形、一般凸图形、外接凸多边形与平行线相交的事件，则有：

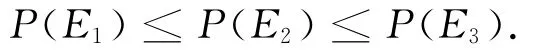
由于外、内接凸多边形无限接近一般凸图形时，三个图形的周长也无限地接近，因此由两边夹原理得到：

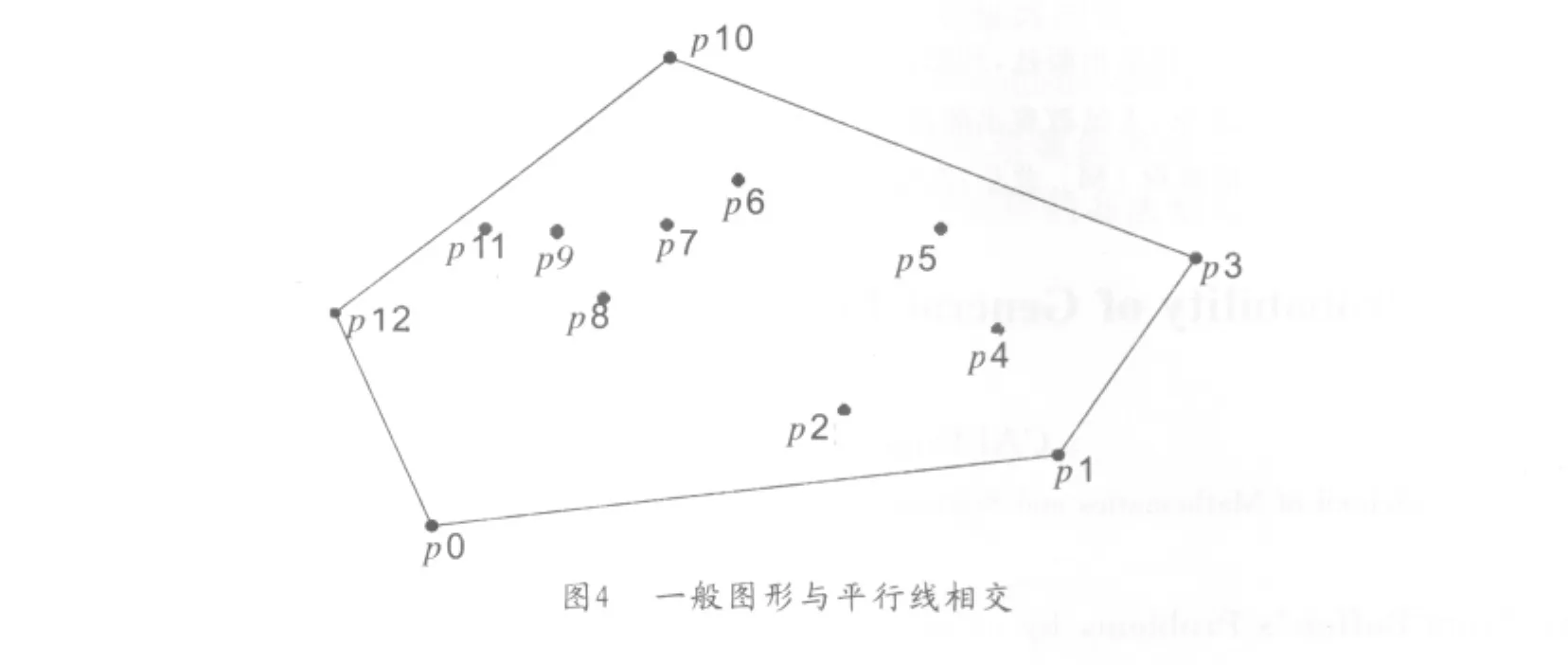
平面上画满间距为a的平行直线，向该平面随机投掷一个一般图形的硬纸片，这里以心形图为例，试问该一般图形与平行线相交的概率．做示意图如图5：

我们可以看到，若这个图形的凸包与平行线相交，那么这个图形与平行线也相交；若这个图形与平行线相交，那么这个一般图形的凸包与平行线也相交．

由凸包的定义我们知道，那是一个能包裹住给定图形的最小的凸多边形，如图4所示．这样我们就可以把研究一般图形与平行线相交的概率问题转化为一般凸图形与平行线相交的概率问题．我们已经知道了一般凸图形与平行线相交的概率：

由此我们可以得到一般图形与平行线相交的概率：

2 结语

本文最终得到了一般的连通图形与平行线相交之概率和其凸包与平行线相交之概率相同的结论，并指出在一定的条件下这一概率与凸包的周长成正比．

［1］杨振明．概率论 ［M］．北京：科学出版社，1999：20～38．

［2］复旦大学．概率论 ［M］．北京：人民教育出版社，1979：38～45．

［3］常庚哲，史济怀．数学分析教程 ［M］．北京：高等教育出版社，2002：150～160．

MSC 2000：60D05

Probability of General Figure Intersecting Parallel Lines

CAI Ding－jiao，BAO Xu-feng
（School of Mathematics and Statistics，Anyang Normal College，Anyang 455002，China）

From Buffon’s Problem，by using the formula calculation of the probability of segment intersecting parallel lines，we get the probability of convex polygon intersecting parallel lines，and then by using approximation theorem，we can get the probability of convex figure intersecting parallel lines，and finally，we point out that the probability of general figure intersecting parallel lines is the same as the probability of its convex hull intersecting parallel lines．

convex polygon；approximation theorem；convex hull

O211．2

A

1009-1734（2011）02-0001-04

2011-02-02

蔡定教，讲师，从事概率论与数理统计研究．