饱和非线性波导阵列的离散孤子＊

黄文华，邱为钢

（湖州师范学院 理学院，浙江 湖州 313000）

饱和非线性波导阵列的离散孤子＊

黄文华，邱为钢

（湖州师范学院 理学院，浙江 湖州 313000）

利用扩展的双曲函数展开法，对饱和离散非线性波导阵列模型离散非线性薛定谔方程进行了研究，获得了多组新的精确解析局域解，包括亮孤子解、暗孤子解，以及亮、暗复合孤子解等，并给出了这些解存在对方程系数的特殊约束关系．

离散饱和非线性薛定谔方程；离散孤子；双曲函数方法

0 引言

自上世纪60年代以来，克尔类型非线性光学媒质的光孤子性质获得了大量的研究成果．这些光学媒质可以用三次非线性薛定谔方程来模拟和描述．众所周知，这种非线性薛定谔方程是可积的，并且孤子间的相互作用是弹性的［1］．近年来，一些学者对像折射媒质的光孤子性质进行了研究［2］，媒质的描述方程模型有异于经典的非线性薛定谔方程，主要在于方程中的克尔非线性项被其他饱和类型项所替代．这种饱和非线性薛定谔方程是不可积的，其孤子的碰撞是非弹性碰撞，可以导致孤子的湮灭、聚变和产生［3～5］．离散的非线性薛定谔方程可以用来描述紧制约束非线性波导阵列．离散非线性薛定谔格子模型中关于移动呼吸子或孤子的存在及其性质研究已经有了许多报道．如文献［6］认为呼吸子能沿着格子传播仅有少量的能量损失，并由于格子的非均匀性会被陷落；继而，更深入的研究认为精确的行波呼吸子至少在一定参数范围内存在［7］．最近，关于饱和离散非线性薛定谔方程描述的像折射晶体波导阵列中的孤子和呼吸子的研究亦有了相应进展的报道［8，9］．该模型系统如下［10］

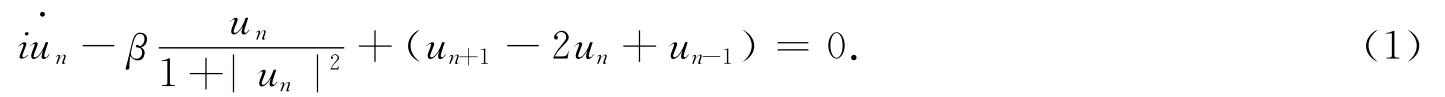
饱和离散非线性薛定谔方程与三次离散非线性薛定谔方程的区别关键在于前者的Peierls-Nabarro势垒是受限制的，而且在大多数情况下要小于后者，这使高能移动孤子得以存在．寻求非线性系统的精确解一直是非线性科学研究的重要课题．由于系统（1）的复杂性，相信还有很多精确解和离散孤子解存在，而获得这些解有助于深入了解像折射媒质饱和波导阵列的光传输特性及光孤子特性．由于非线性离散差分方程的特点，求其精确解相对而言比连续非线性偏微分方程要更加困难．本文利用新近提出的求解非线性离散差分方程的所谓扩展的双曲函数方法［11］对方程（1）进行进一步研究，获得了新的精确解和离散孤子．

1 方程（1）的精确解

为了获得离散的饱和非线性薛定谔方程（1）的精确解，首先做以下行波变换：

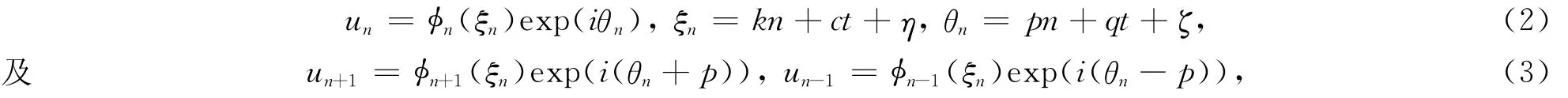
其中k，c，p，q，n，η，ζ为实常数．将变换（2）和（3）代入方程（1），利用诱导公式：

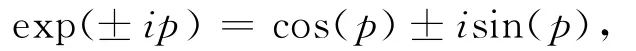
经整理，令方程虚部和实部都等于零，可以得到：

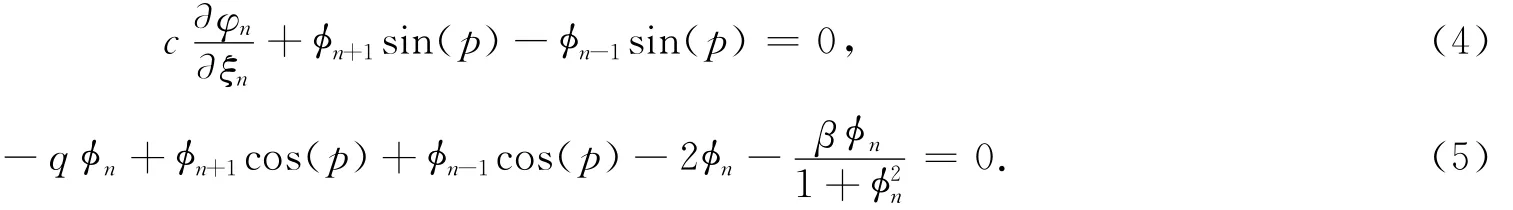
为得到方程（4）和（5）的精确解，利用扩展的双曲函数展开法，基于奇次平衡原则，平衡最高阶微分项和非线性项，可以假定φn有如下形式的解：

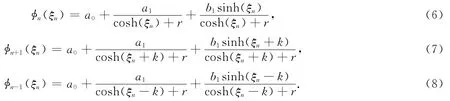
其中a0，a1，b1和r为待求实常数．将（6）、（7）式代入方程（4）和（5），合并各同阶项

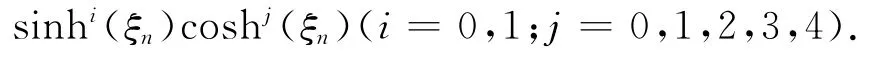
并令其系数为零，可以得到一组关于a0，a1，b1，k，c，p，q，r的代数方程．为避免繁冗，这里略去该超定代数方程组，借助数学符号运算软件Maple，直接给出求解方程组所得解：

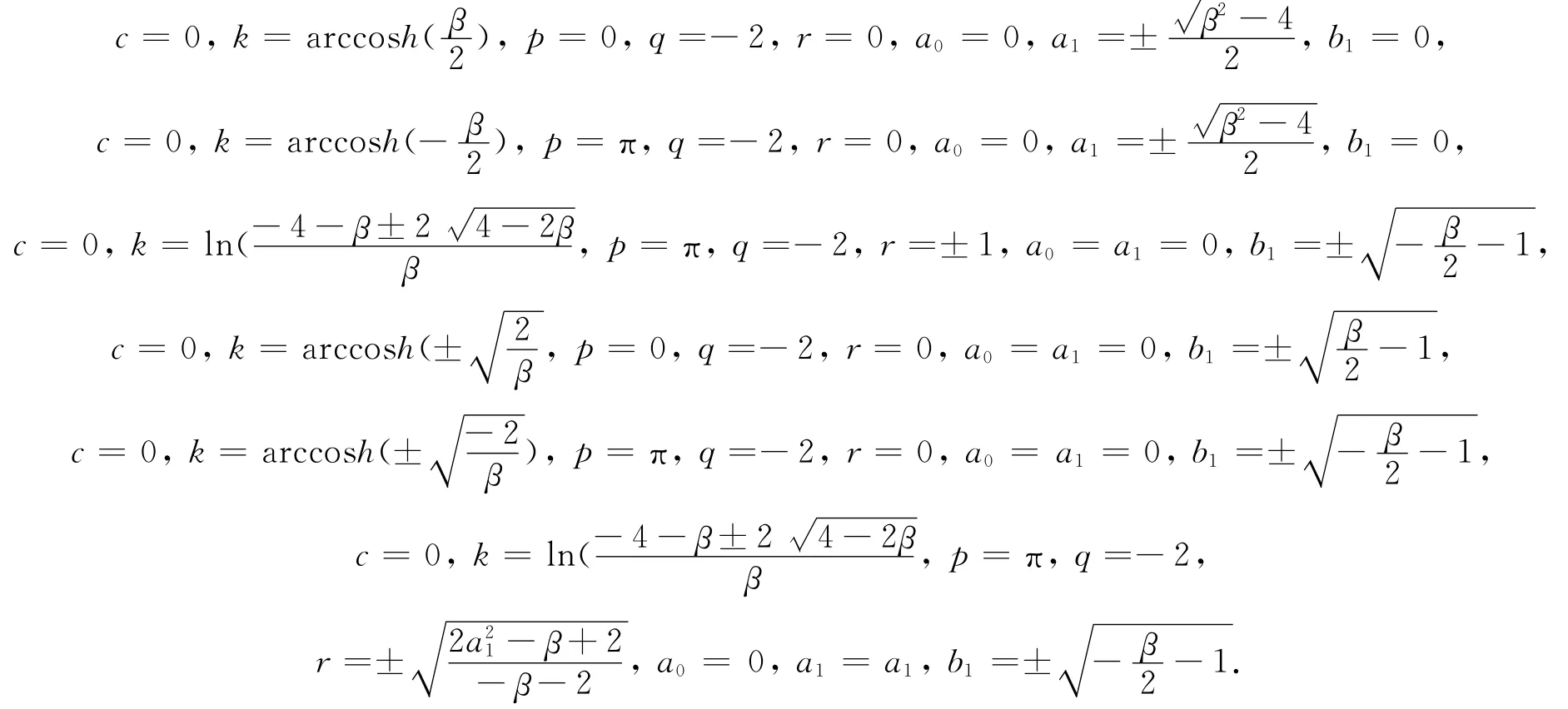
将上述关于a0，a1，b1，k，c，p，q，r的结果代入（6）和（2）式，最终可以得到饱和离散非线性薛定谔方程（1）的精确孤子解．

亮孤子解：

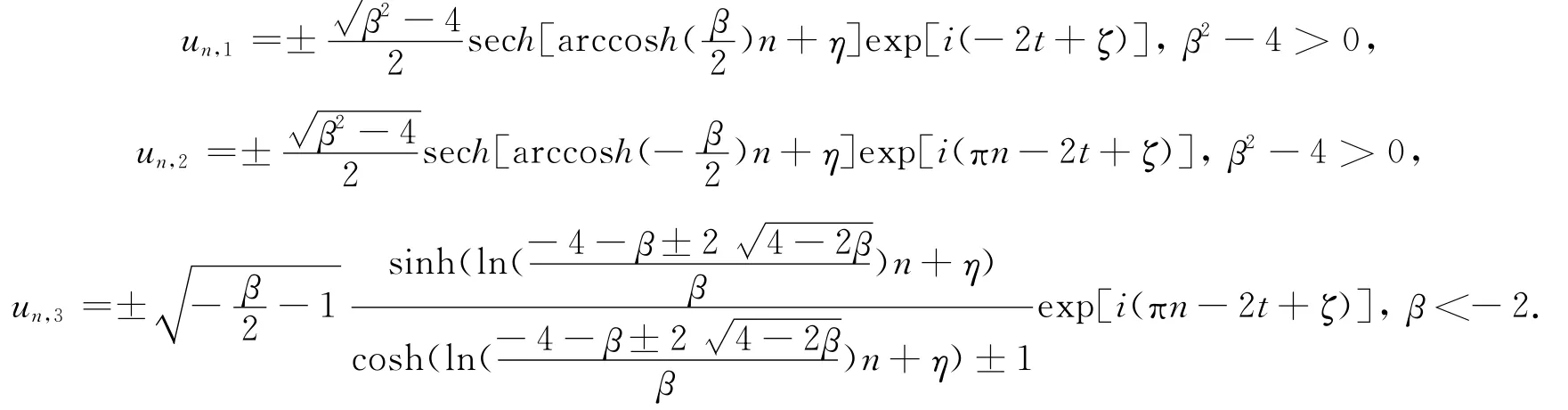
暗孤子解：

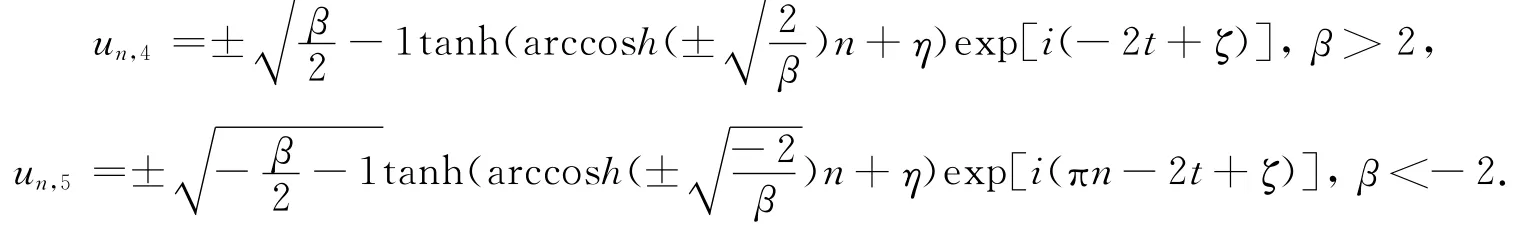
亮、暗复合孤子解：

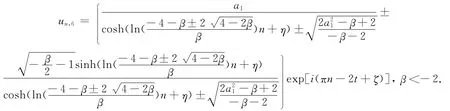
2 结论

利用扩展的双曲函数展开法对饱和非线性波导阵列模型离散非线性薛定谔方程进行了研究，获得了6组新的精确解析局域解．这些局域解包括亮孤子解、暗孤子解以及亮、暗复合孤子解．对于饱和离散非线性薛定谔方程系统，存在另一方程形式如文献［12］中描述的

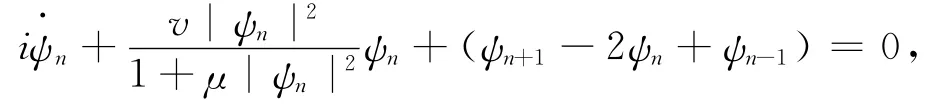
由于该模型与方程（1）是非独立的，可以建立以下映射关系

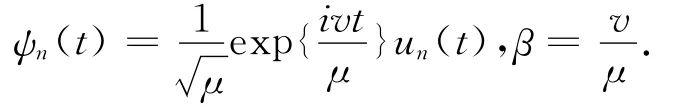
因而利用本文所得结果很容易获得这一模型相应的离散孤子解．这对于进一步研究饱和非线性波导阵列，研究离散孤子性质及相互作用，具有十分重要的意义，相应研究将另文进一步展开．扩展的双曲函数展开法可以有效求解离散差分系统，值得在其他非线性离散模型中推广应用．

［1］ZAKHAROV V E，SHABAT A B．Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media［J］．Sov Phys JETP，1972，34：62～69．

［2］KRÓLIKOWSKI W，LUTHER-DAVIES B，DENZ C．Photorefractive solitons［J］．IEEE J Quantum Electron，2003，39：3～12．

［3］SNYDER A W，SHEPPARD A P．Collisions，steering，and guidance with spatial solitons［J］．Opt Lett，1993，18：482～484．

［4］KRÓLIKOWSKI W，HOLMSTROM S A．Fusion and birth of spatial solitons upon collision［J］．Opt Lett，1997，22：369～371．

［5］JAKUBOWSKI M H，STEIGLITZ K，SQUIER R．Information Transfer between Solitary Waves in the Saturable Schrödinger Equation［J］．Phys Rev E，1997，56：7267～7273．

［6］EILBECK J C，KAWABATA C，BISHOP A R．Computer Analysis for Life Science-Progress and Challenges in Biological and Synthetic Polymer Research［M］．Tokyo：Ohmsha，1986：12～21．

［7］REMOISSENET M，PEYRARD M．Nonlinear Coherent Structures in Physics and Biology［M］．Berlin：Springer，1991：159～167．

［8］HADZIEVSKI L，MALUCKOV A，STEPIC M，et al．Power Controlled Soliton Stability and Steering in Lattices with Saturable Nonlinearity［J］．Phys Rev Lett，2004，93：033901．

［9］STEPIC M，KIP D，HAPZIEVSK I L，et al．One-dimensional bright discrete solitons in media with saturable nonlinearity［J］．Phys Rev E，2004，69：066618．

［10］CUEVAS J A，EILBECK C．Discrete soliton collisions in a waveguide array with saturable nonlinearity［J］．Physics Letters A，2006，358：15～20．

［11］BAI C L，LI Y．A simple but efficient approach for studying on nonlinear differential-difference equations［J］．Chaos，Solitons and Fractals，2009，39：130～135．

［12］KHARE A，RASMUSSEN K，SAMUELSEN M R，et al．Exact solutions of the saturable discrete nonlinear Schrodinger equation［J］．J Phys A：Math Gen，2005，38：807～810．

Discrete Soliton in a Waveguide Array with Saturable Nonlinearity

HUANG Wen-Hua，QIU Wei-gang
（School of Science，Huzhou Teachers College，Huzhou 313000，China）

By applying extended hyperbolic function method，we study the saturable discrete nonlinear Schrodinger equation and obtained a number of new exact localized solutions，including discrete bright soliton solution，dark soliton solution，bright and dark soliton solution，and provide that a special relation is bound on the coefficients of the equation among the solutions obtained．

the saturable discrete nonlinear Schrodinger equation；discrete soliton；hyperbolic function method

O175．29

A

1009-1734（2011）02-0051-04

2011-03-16

浙江省教育厅科研项目（Y200908781）．

黄文华，副教授，博士，从事非线性物理研究．