基于BP网络的有教师分类算法及应用

唐凤仙，汤鹏杰

(河池学院 计算机与信息科学系，广西 宜州 546300)

基于BP网络的有教师分类算法及应用

唐凤仙，汤鹏杰

(河池学院 计算机与信息科学系，广西 宜州 546300)

介绍BP神经网络的结构及相关算法，并通过实验比较不同情况下对BP神经网络的收敛速度与分类精度的影响。实验表明，合适的参数设置能提高BP神经网络算法的分类精度。

BP网络;激活函数;训练;分类精度

0 引言

近些年来，神经网络一直是人工智能中研究的一个热点问题。一个神经网络是一个由简单处理单元构成的规模宏大的并行分布式处理器。人工神经网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。人工神经网络具有自学习和自适应的能力，可以通过预先提供的一批相互对应的输入—输出数据，分析掌握两者之间潜在的规律，最终根据这些规律，用新的输入数据来推算输出结果。在人工神经网络发展历史中，很长一段时间里没有找到隐层的连接权值调整问题的有效算法，直到误差反向传播算法(BP算法)的提出，成功地解决了求解非线性连续函数的多层前馈神经网络权重调整问题［1，2］。BP神经网络是人工神经网络精华，广泛应用于模式识别、人工、智能、控制工程、信号处理等领域［3］。

1 BP神经网络结构

BP神经网络是一种神经网络学习算法，其全称为基于误差反向传播算法的人工神经网络。如图1所示结构的单隐层前馈网络，一般称为三层前馈网或三层感知器，即:输入层、中间层(也称隐层)和输出层。它的特点是:各层神经元仅与相邻层神经元之间相互全连接，同层内神经元之间无连接，各层神经元之间无反馈连接，构成具有层次结构的前馈型神经网络系统。单计算层前馈神经网络只能求解线性可分问题，能够求解非线性问题的网络必须是具有隐层的多层神经网络［4，5］。

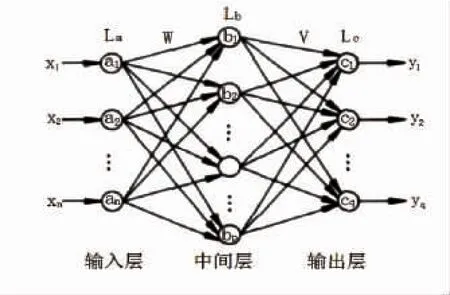
图1 最简单的BP神经网络结构

BP算法的基本思想是，学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时，输入样本从输入层传入，经各中间层逐层处理后，传向输出层。若输出层的实际输出与期望的输出(教师信号)不符，则转入误差的反向传播阶段。误差反传是将输出误差以某种形式通过中间层向输入层逐层反传，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号作为修正各单元连接权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程，是周而复始地进行的。连接权值不断调整的过程，也就是网络学习训练过程，此过程一直进行到网络输出的误差减少到可接受的程度，或进行到预先设定的学习次数为止，即按有教师示教的方式进行学习［6，7］。

2 BP算法及应用

BP神经网络以其独特的优势，在许多领域得到广泛应用，本文实验主要以其在模式识别中的应用为例，实验数据为Iris数据。

2.1 结构设计

由于Iris数据最后有三类，所以设计的模型是一个多类的分类器。使用的方法是，用两个输出节点c1，c2对应LB层两个节点输出组合，得到最终的分类结果。其结构图如图2。

其中:(1)LA为输入层，由于Iris的数据项为4个，故该层单元数:LANUM=4。

(2)LB为隐含层，该层单元数设为:LBNUM。

(3)LC为输出层，由于Iris的数据总共分为3类，因此:LCNUM=2。

图2 BP神经网络结构图

(4)weighAB为 LA→LB的连接权重，weighBC为LB→LC的连接权重。

2.2 数据预处理及参数初始化

数据预处理与激活函数的定义有很大关系。神经网络比较通用的两种激活函数是S型激活函数f(x)=而用这两种激活函数，由于产生的输出是二值的，即只能做二类问题的求解。而所给定的Iris数据集总共有三类。也就是说，必须设定两个输出节点，通过两个输出节点的组合来达到三类的分类效果。因而要对Iris数据集预处理，根据所用的激活函数的不同，Iris在用S型激活函数时，分类标注用(0，0)表示第一类，(0，1)表示第二类，(1，1)表示第三类;在双曲正切激活函数时，分类标注用(1，1)表示第一类，(1，－1)表示第二类，(－1，－1)表示第三类。这样数据与输出达到统一。

算法参数主要包括学习率的选择，权重矩阵的选择。权重矩阵的初始化对整个学习效果有至关重要的作用，方法如下:

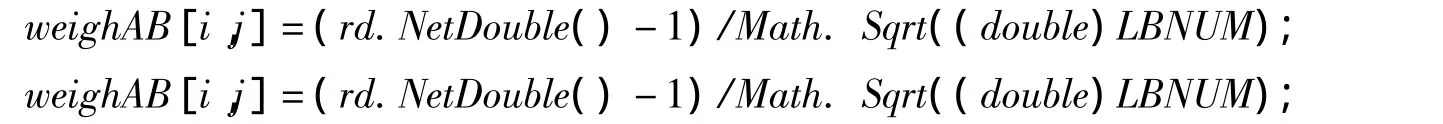
2.3 神经网络的训练

样本的训练包括每一层输出计算、误差计算和权重学习修正、迭代训练。

(1)隐节点i即LB层节点i的输入为:

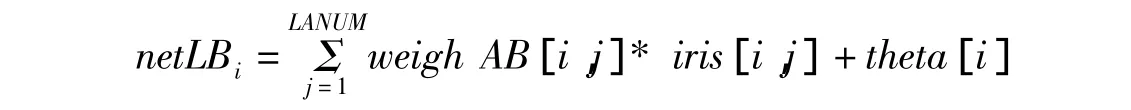
(2)LB层节点i的输出为:

(3)输出节点j即LC节点j的加权输入为:

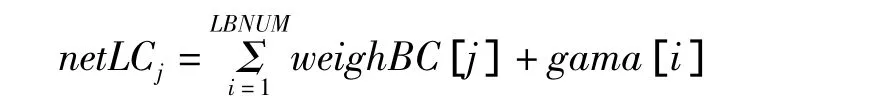
(4)LB层节点i的输出为:

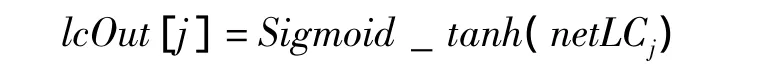
其中sigmoid_tanh为定义的激活函数，如前所述，根据选择的结果，或为S型，或为双曲正切函数;iris［t，j］为第t个Iris样本;gama和theta分别为LC和LB节点的阈值矩阵。

2.4 误差计算

根据采用不同的准则函数和激活函数，所计算的误差方法也不相同。误差平方和准则下的误差计算［6］，定义全局代价函数为:

2.5 权重学习修正

权重的修改值也可以由全局代价函数得到:

2.6 迭代训练，建立最终模型

利用累积误差反传播算法，计算所有样本的权重总变化值，并计算总误差，算总迭代一次，根据总权重变化值修正权重，再由总误差判断迭代条件。在迭代停止时，即建立好模型。关键代码如下:

3 实验结果与分析

本文实验全部在运行Windows XP操作系统和Microsotf visual studio 2008软件的计算机上进行。实验数据为Iris数据集。实验方案为:(1)误差阈值对收敛速率与分类精度的影响，(2)激活函数对分类精度的影响，(3)学习率对收敛速率及分类精度的影响，(4)隐层结点个数对收敛速率及分类精度的影响。

3.1 误差阈值对收敛速率与分类精度的影响

本次实验中隐层节点个数为3，使用S型函数作为激活函数，使用误差平方和准则，对比误差阈值对收敛速率与分类精度的影响，实验结果如表1所示。

表1 误差阈值对收敛速率与分类精度的影响

实验结果表明，随着误差阈值的减小，达到收敛所需的修正次数增加，分类精度有所提高。

3.2 激活函数对分类精度的影响

本次试验中隐层节点个数为3，固定修正次数为5 000次，使用误差平方和准则。对比激活函数对分类精度的影响，实验结果见表2。

表2 激活函数对分类精度的影响

实验结果表明，对于Iris数据集，使用S型函数作为激活函数能达到较高的分类精度。

3.3 学习率对收敛速率及分类精度的影响

本实验隐层节点个数为3，固定训练误差阈值0.5，S型函数作为激活函数，研究学习率对收敛速率及分类精度的影响。比较使用的两种学习率为:静态学习率和动态学习率。

(1)静态学习率在每次修正时都使用相同的学习率:alpha=0.01;beta=0.001。

(2)动态学习率在每次修正时根据误差的不同，使用不同的学习率。学习率的初值为alpha=0.01;beta=0.001;每次修正时，根据误差改变学习率:alpha=alpha*Math.Exp(e*2);beta=alpha*Math.Exp(e*2);其中e为误差。

表3 学习率对收敛速率及分类精度的影响

实验结果表明，动态学习率的收敛速率远远高于静态学习率，动态学习率的分类精度略高于静态学习率。

3.4 隐层结点个数对收敛速率及分类精度的影响

本实验固定训练误差阈值0.5，S型函数作为激活函数，使用动态学习率，研究隐层结点个数对收敛速率及分类精度的影响。

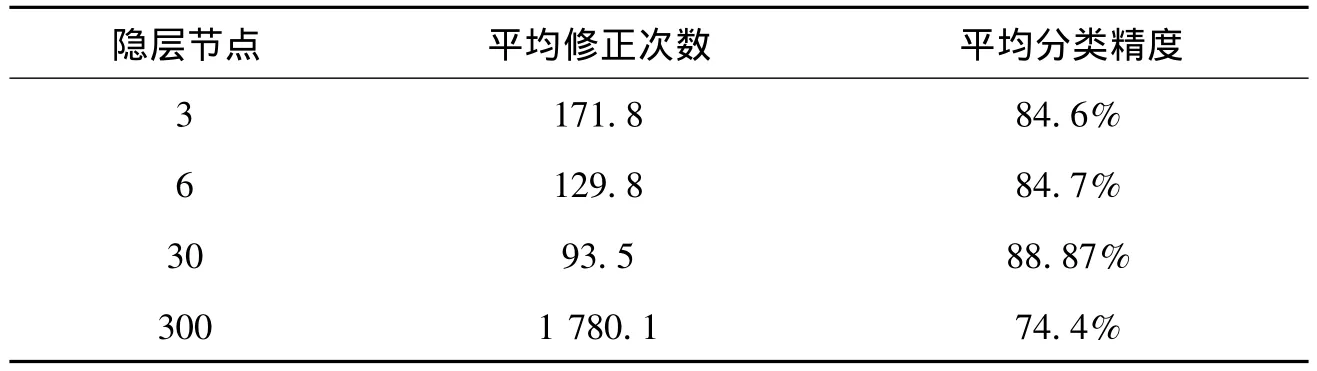
表4 隐层结点个数对收敛速率及分类精度的影响

实验结果表明，合适的隐层节点数能达到较高的收敛速率和分类精度(本例中取30比较合适)，但过多的隐层节点数会导致收敛速率和分类精度的下降。

4 结束语

实验表明，通过调整不同的参数，BP神经网络具有良好的分类效果。当然，单隐层的BP网络是最简单的BP网络，只能解决线性可分的分类问题。对于线性不可分的分类问题，还要借助多隐层及其他辅助技术来实现［8］，另外由于其自身的缺点所在［9］，其算法的改进，网络优化还有待更深入的研究。

［1］李爱军.前馈神经网络工作机理分析与学习算法［M］.北京:中国科学技术出版社，2006.

［2］罗晓曙.人工神经网络理论·模型·算法与应用［M］.桂林:广西师范大学出版社，2005.

［3］祝翠玲，蒋志方，王强.基于B－P神经网络的环境空气质量预测模型［J］.计算机工程与应用，2007，43(22):223－227.

［4］田景文，高美娟.人工神经网络算法研究及应用［M］.北京:北京理工大学出版社，2006.

［5］高济.人工智能高级技术导论［M］.北京:高等教育出版社，2009.

［6］胡伍生.神经网络理论及其工程应用［M］.北京:测绘出版社，2006.

［7］(俄)А.И.加卢什金.神经网络理论［M］.阎平凡，译.北京:清华大学出版社，2002.

［8］张代远.神经网络新理论与方法［M］.北京:清华大学出版社，2006.

［9］宋振宇，王秋彦，丁小峰.BP神经网络训练中的实际问题研究［J］.海军航空工程学院学报，2009，24(6):704－707.

The Teacher Classification Algorithm and Application Based on BP Neural Network

TANG Feng-xian，TANG Peng-jie
(Department of Computer and Information Science，Hechi University，Yizhou，Guangxi 546300，China)

This Paper describes the structure of BP neural network and related algorithms，and then compares the convergence rate of BP neural network and classification accuracy under different conditions through experiments.The results show that the appropriate BP parameters can improve the classification accuracy of neural network algorithm.

BP neural network;activation function;training;classification accuracy

TP183

A

1672－9021(2011)02－0041－05

唐凤仙(1977－)，女，广西都安人，河池学院计算机与信息科学系讲师，主要研究方向:模式识别，图像处理。

广西壮族自治区教育厅科研立项项目(201010LX482)。

2010－03－01

［责任编辑 刘景平］