许用载荷求解方法的优化

刘明超 丁晓燕

（1山东大学土建与水利学院，山东 济南 250100）

（2北京理工大学机电学院，北京 102400）

许用载荷求解方法的优化

刘明超1丁晓燕2

（1山东大学土建与水利学院，山东 济南 250100）

（2北京理工大学机电学院，北京 102400）

计算方法的优化是人们对问题通过多途径分析，找到能使计算步骤简单，易于使结果准确的方法，在理论分析和工程实践中具有十分重要的意义.本文试图通过对一个实例的分析，提出一种优化材料许用载荷求解的方法，通过此方法可以减少工程中许用载荷计算的工作量，有助于提高计算效率.

许用载荷；工程；优化方法

1 引例

例1如图1所示，长为L，重为W 的杆AB支撑住位于光滑竖直倒槽内的物块E，物块E重G；A、B接触面的静摩擦系数均为μ.求杆AB能保持平衡的最大角度φ.

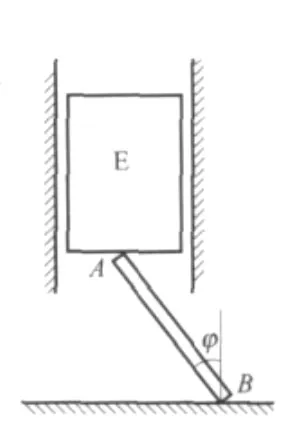
图1

文献［2］中给出的解法为穷举法，如下所列的解法（1）.

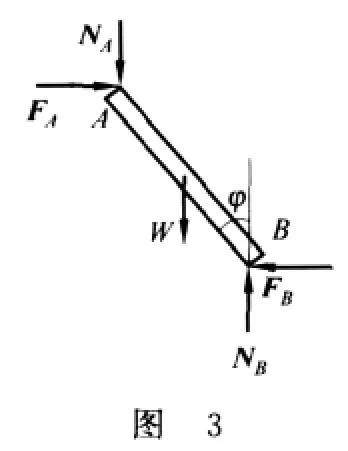
解法（1）

（1）设B点先达到临界状态，A点未达到，则有

取物块E进行受力分析，有

取杆AB进行受力分析，有

由方程（1）～（4），得

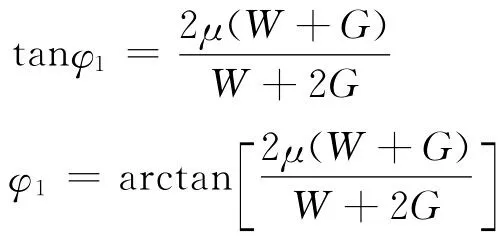
（2）设A点先达到临界状态，B点未达到，则有

取杆AB进行受力分析，有

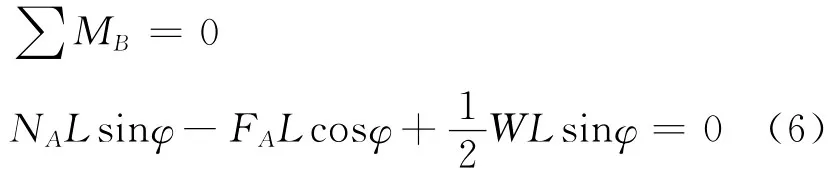
由方程（2）、（3）、（5）、（6），得

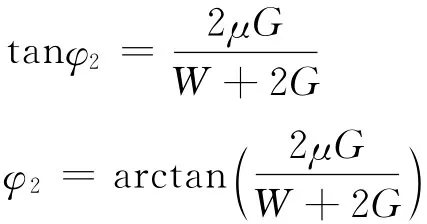
比较φ1和φ2可知，使杆AB保持平衡的最大夹角此时杆A处于临界状态.

下面，我们对此解法进行优化.

解法（2）

先分析A、B两杆的受力情况，由解法（1）知：

对E：NA＝G，对AB：NB＝G＋W，即A处的支持力恒小于B处.由于A、B接触面静摩擦系数相同，故由Ff＝μFN知，A处一定先达到临界状态，即有FA＝μNA.

再对AB杆进行受力分析：

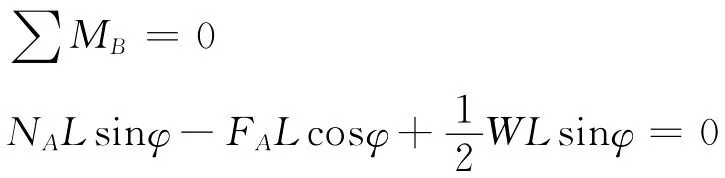
不难看出，解法（2）通过先分析受力情况而排除了“B点先达到临界状态，A点未达到”的情况，简化了求解过程，达到了优化计算方法的效果.

2 许用载荷计算方法的优化

下面，我们将此优化方法的思路推广到材料许用载荷计算的一类问题中.

例2如图4所示，两杆三角支架中杆AB和杆BC的材料相同，均为直径为D的圆截面，材料的许用应力为［σ］，试确定结构的许用载荷［F］.

通常采用类似于例1中的穷举法，如下所列的解法（1）.

解法（1）

（1）求各杆中轴力的表达式

对A节点（图5）列写平衡方程，求得

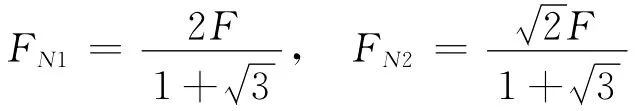
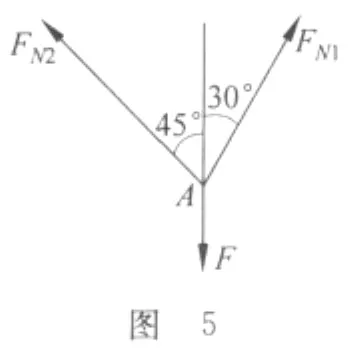
（2）根据强度条件确定许用载荷

对AB杆，有

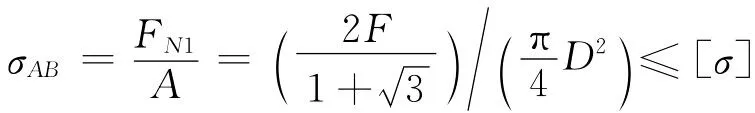
故保证杆AB安全的许用载荷为

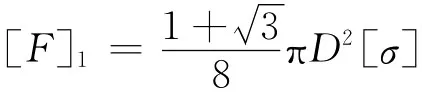
对AC杆，有

故保证杆AC安全的许用载荷为

综上，保证两杆均安全的许用载荷应取

很明显，上述解法不是最简的，按照例1的思路，我们可以对其作如下优化.

解法（2）

保证两杆均安全则只需保证杆AB安全，由

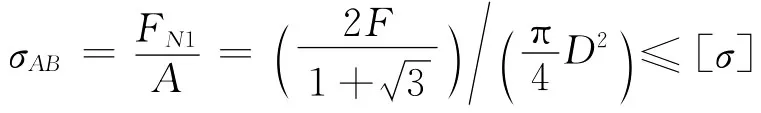
得许用载荷为

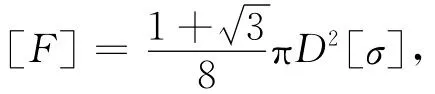
结论与解法（1）相同.

3 总结

由上述例2可以看出，通过分析不同杆的受力情况，对求解方法进行优化，可以简化求解过程，减少计算量.

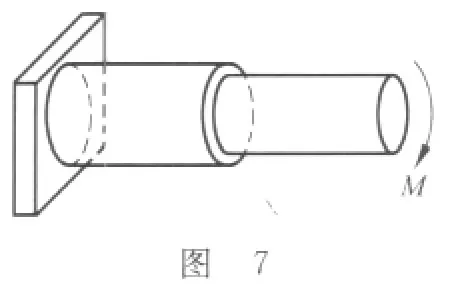
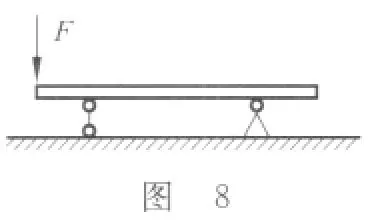
此例给出的只是两杆的情况，对于多杆求拉压许用载荷的情况，只要杆的材料和横截面相同，均可只计算轴力最大杆的许用载荷，这样就可以减少大量的运算.例如，在计算图6所示的房屋立柱（材料和尺寸均相同）的许用压应力时，若顶面力系均匀分布（图6（a）），则只需计算其中一根立柱的许用压应力；若顶面力系非均匀分布（图6（b）），则只需找出受力最大的一根立柱，计算其许用压应力.这样的实例在工程实践中还有很多.同样，对于相同材料尺寸非均匀的圆轴（图7），计算许用载荷时只需找出其中的危险截面，按危险截面处应力状态求许用载荷.对于相同材料等截面梁的弯曲问题（图8），计算许用载荷同样只需考查危险截面处即可.

图6

本文只讨论计算许用载荷方法的优化，其实，这种思路还可以应用到强度校核中，同样可以达到很好的优化效果.

［1］ 韩斌，刘海燕等.材料力学［M］.北京：兵器工业出版社，2009.101～208

［2］ 高云峰，蒋持平等.力学小问题及全国大学生力学竞赛试题［M］.北京：清华大学出版社，2003.25～26

［3］ 刘鸿文.材料力学Ⅰ［M］.北京：高等教育出版社，2004.12～49

2011－04－26）

刘明超（1990年出生），男，四川广元人，山东大学土建与水利学院工程力学专业2009级本科生（2010至2011学年在北京理工大学交流学习）；丁晓燕（1989年出生），女，山东烟台人，北京理工大学机电学院工程力学专业2009级本科生.